Anteriormente en nuestro blog, publicamos un artículo en el que, a modo de introducción, explicábamos la base matemática que hay tras el PCA: Análisis de Componentes Principales: Una breve introducción matemática.
En esta segunda parte, dejaremos la parte teórica y veremos un ejemplo sencillo. Hay diversos lenguajes de programación con paquetes que incluyen PCA. Nosotros utilizaremos Python junto con la librería scikit-learn.
Conjunto de datos: Iris
Utilizaremos el dataset Iris para ilustrar el ejemplo. Podemos cargar el conjunto de datos desde la librería seaborn. Vamos a cargar las librerías que necesitaremos, leer el dataset y mostramos las cinco primeras filas del dataset para visualizar cómo son los datos.
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
%matplotlib inlineiris = sns.load_dataset("iris")
iris.head()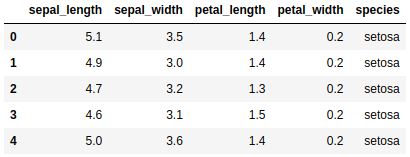
Uno de los requisitos que explicamos anteriormente es que las variables estén correlacionadas para obtener una representación más simple de éstas.
iris.corr()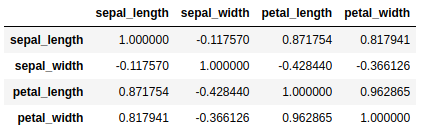
Estandarización
Necesitamos que las variables numéricas estén estandarizadas porque se observa una diferencia de magnitud entre ellas. Podemos ver que petal_width y sepal_length están en magnitudes totalmente distintas, con lo cual a la hora de calcular los componentes principales sepal_length va a dominar a petal_width por la mayor escala de magnitud y, por tanto, mayor rango de varianza.
X = iris.loc[:, ["sepal_length", "sepal_width", "petal_length", "petal_width"]]
Y = iris.loc[:, ["species"]]
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)El paquete sklearn.preprocessing contiene la clase StandarScaler que nos permite escalar nuestras variables.
PCA
Cálculo de los componentes principales
Una vez que tenemos nuestras variables numéricas estandarizadas, es hora de proceder con el cálculo de los componentes principales. En este caso, vamos a elegir dos componentes principales por la simple razón de que este es un ejemplo sencillo y queremos visualizar en dos dimensiones más adelante.
from sklearn.decomposition import PCA
PCA = PCA(n_components=2)
components = PCA.fit_transform(X)
PCA.components_
La clase PCA del paquete sklearn.decomposition nos proporciona una de las maneras de realizar el análisis de componentes principales en Python.
Para ver cómo se relacionan los componentes principales con las variables originales, mostramos los vectores propios o loadings. Vemos que el primer componente principal da casi el mismo peso a sepal_length, petal_length y petal.width, mientras que el segundo componente principal da peso primordialmente a sepal_width.
Varianza explicada
Además, podemos ver con los valores propios la varianza explicada por los dos componentes principales y la varianza explicada acumulada.
cumVar = pd.DataFrame(np.cumsum(PCA.explained_variance_ratio_)*100,
columns=["cumVarPerc"])
expVar = pd.DataFrame(PCA.explained_variance_ratio_*100, columns=["VarPerc"])
pd.concat([expVar, cumVar], axis=1)\
.rename(index={0: "PC1", 1: "PC2"})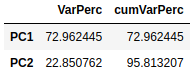
El primer componente principal explica un 72.96% de la variación total de los datos originales, mientras que el segundo explica un 22.85%. Conjuntamente, los dos componentes principales explican alrededor del 95.81% de la variación total, un porcentaje bastante elevado.
Visualización
En este apartado vamos a realizar dos gráficos para visualizar: un diagrama de dispersión y un biplot.
El diagrama de dispersión nos sirve para ver los valores de las observaciones respecto de los dos componentes principales y resaltamos las diferentes observaciones por su especie.
componentsDf = pd.DataFrame(data = components, columns = ['PC1', 'PC2'])
pcaDf = pd.concat([componentsDf, Y], axis=1)
plt.figure(figsize=(12, 6))
sns.scatterplot(data=pcaDf, x="PC1", y="PC2", hue="species")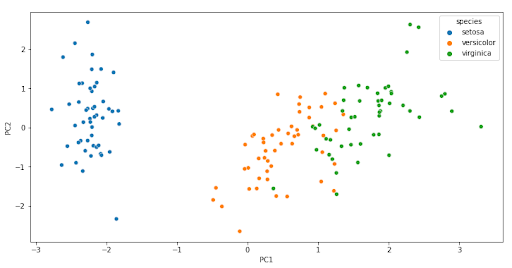
Vemos que existe una clara separación entre los diferentes tipos de especies que hay. Cada clase de flor representa un clúster específico y en el gráfico se puede ver esa distribución.
El biplot es un gráfico que permite representar las variables del dataset original y las observaciones transformadas en los ejes de los dos componentes principales. Las flechas representan las variables originales y es importante hacia dónde apuntan. La dirección y el sentido indican el peso y el signo de las variables originales en los dos componentes principales.
Varias cosas que podemos comentar sobre las flechas son:
- Dos flechas que tienen dirección y sentido semejantes indica una correlación positiva.
- Dos flechas que tienen la misma dirección pero sentidos diferentes indican una correlación negativa.
- Un ángulo recto (90º) entre dos flechas indica no correlación entre ellas.
- Un ángulo llano (180º) entre dos flechas indica correlación negativa perfecta.
Para calcular el biplot necesitamos definir antes la función que realizará el plot, para después mostrar el gráfico.
def biplot(score,coeff,labels=None):
xs = score[:,0]
ys = score[:,1]
n = coeff.shape[0]
scalex = 1.0/(xs.max() - xs.min())
scaley = 1.0/(ys.max() - ys.min())
plt.scatter(xs * scalex,ys * scaley,s=5)
for i in range(n):
plt.arrow(0, 0, coeff[i,0], coeff[i,1],color = 'r',alpha = 0.5)
if labels is None:
plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, "Var"+str(i+1), color = 'green', ha = 'center', va = 'center')
else:
plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, labels[i], color = 'g', ha = 'center', va = 'center')
plt.xlabel("PC{}".format(1))
plt.ylabel("PC{}".format(2))
plt.grid()plt.figure(figsize=(12, 6))
biplot(components, np.transpose(PCA.components_), list(iris.columns))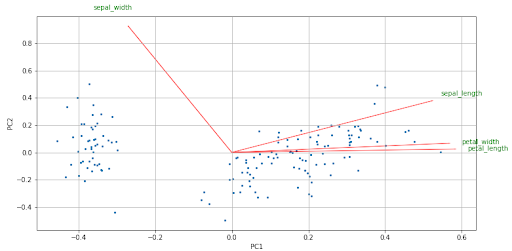
Vemos en el biplot el tamaño de las flechas, es un indicativo de que todas las variables originales tienen cierto peso en los componentes principales.
Además, vemos que hay una correlación positiva entre sepal_length, petal_width y petal_length, mientras que sepal_length y sepal_width tienen una correlación pequeña ya que el ángulo que forman las dos flechas es casi recto.
Entre petal_length y sepal_width hay una correlación negativa, de la misma forma que petal_width y sepal_width. El tamaño y la dirección en la que apuntan las flechas nos indican el peso (positivo o negativo) y la influencia que tiene cada variable en los dos componentes principales.
Conclusión
Junto con el primer post, hemos podido dar una visión general del método con su explicación matemática para después ilustrar su aplicación en Python con un ejemplo sencillo.
Hemos conseguido reducir la dimensionalidad de nuestro conjunto de datos y podemos realizar gráficos, pero no todo es bonito. La interpretabilidad de los componentes principales es difícil, ya que es una combinación lineal de las variables originales y en general no sabremos qué indican estos componentes.
Si este artículo te ha parecido interesante, puedes pasarte por la categoría Algoritmos de nuestro blog para ver más posts similares a este.

