Los sistemas de fijación de precios que actualmente se usan en las empresas tienen una diferencia sustancial con respecto a los que había hace 20 años. Hemos pasado de sistemas de fijación de precios estáticos, es decir, de precios constantes en diferentes momentos del año, a sistemas dinámicos, donde los precios pueden variar en función de múltiples factores como la demanda, la competencia, stock disponible y un largo etcétera.
Es común lidiar con este dinamismo mediante sistemas de reglas complejas que pueden hacer que para un solo día se activen múltiples reglas, entre las cuales puede haber incompatibilidades. Es decir, cuando se pierde el control sobre las reglas generadas debido a su gran volumen, es posible que ocurran incoherencias como que ciertas reglas no puedan ejecutarse nunca debido a que son incompatibles con otras que tienen mayor orden de importancia.
En este artículo, trabajaremos con una prueba de concepto simplificada para tratar de identificar qué reglas son factibles y cuáles no lo son.
Contexto de la demo
Trabajaremos con reglas de precios para dos productos, A y B, y las dimensiones, es decir, los campos que determinan si se activan o no dichas reglas será el día de la semana. Sin embargo, como hemos comentado anteriormente, la cantidad de dimensiones que podrían hacer que se activen las reglas pueden ser muchas y muy variadas.
Los días para los que estudiaremos qué reglas se deben aplicar son 2024-06-30, que es un domingo, y 2024-07-01, que es un lunes.
Tipos de reglas
En esta demo trabajaremos con dos tipos de reglas: absolutas y relativas. Las reglas absolutas consisten en poner un precio máximo o mínimo de un cierto producto. El matiz importante es que estas reglas sólo contienen información de un solo producto por regla. Por otro lado, trabajaremos con reglas relativas, las cuales, en nuestra demo, hacen referencia a dos productos por regla (se ha elegido dos productos para simplificar un poco la demostración, pero trabajar con más de dos productos por regla no supone ningún inconveniente).
Cada regla tiene una importancia asignada. La interpretación que se le ha dado es que cuanto menor es este valor, mayor es la importancia de la regla.
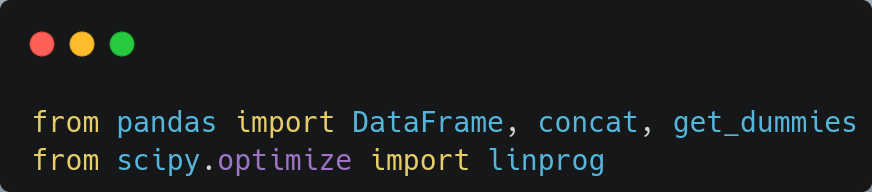
Empecemos importando las dependencias necesarias de toda la demo:
Reglas absolutas
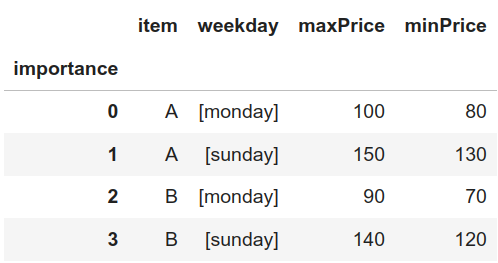
Se han creado dos reglas absolutas por producto:
- Producto A:
- El lunes debe costar entre 80 y 100.
- El domingo debe costar entre 130 y 150.
- Producto B:
- El lunes debe costar entre 70 y 90.
- El domingo debe costar entre 120 y 140.
Estas reglas deben procesarse para identificar cuáles aplican para cada día de interés. En nuestro caso, el resultado de este proceso es el siguiente:
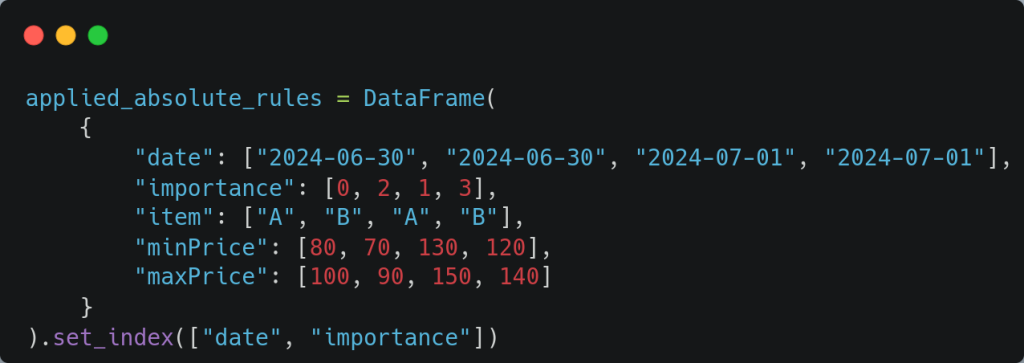
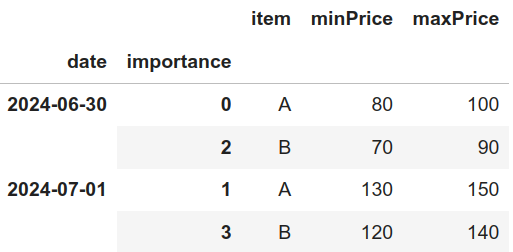
Es decir, para el día de interés 2024-06-30, las reglas absolutas que aplican son las que tienen importancia 0 y 2. Por otro lado, para el día de interés 2024-07-01, las reglas absolutas que aplican son las que tienen importancia 1 y 3.
Reglas relativas
Se han creado dos reglas relativas:
- Los lunes, el producto B debe tener entre un 5% y un 10% de descuento con respecto al producto A. Es decir, como máximo el producto B debe costar el precio del producto A con un 5% de descuento aplicado y, como mínimo, debe costar el precio del producto A con un 10% de descuento aplicado.
- Los domingos, el porcentaje de descuento máximo anterior pasa del 10% al 20%. El mínimo porcentaje de descuento se mantiene igual que en la regla anterior, es decir, es de un 5%.
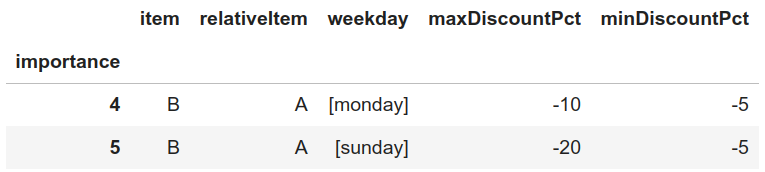
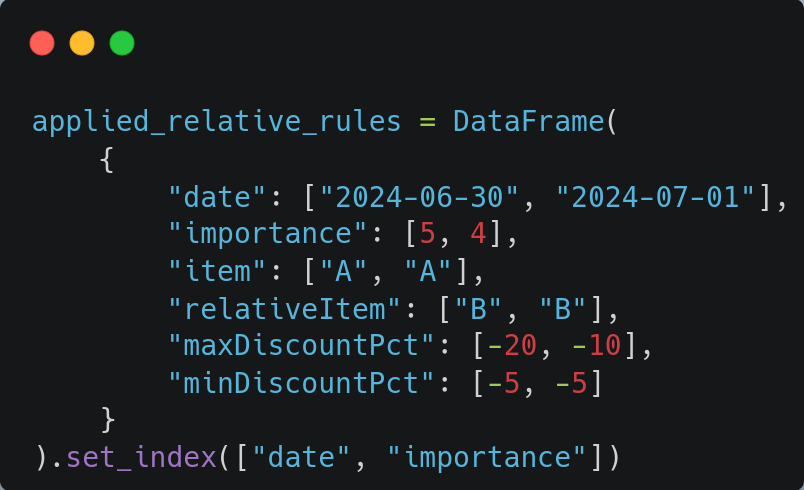
Al igual que con las reglas absolutas, estas reglas deben procesarse cada día que se quiera estudiar qué reglas aplican. En nuestro caso, el resultado de este proceso es el siguiente:
Matriz de restricciones
La matriz de restricciones es la representación numérica de las reglas. Tiene las siguientes características:
- Cada fila consiste en una regla de desigualdad de tipo “menor que” donde a la izquierda de la desigualdad tenemos todos los términos que dependen del precio de un producto y a la derecha de la misma tenemos el término que no depende del precio de ningún artículo, también denominado término independiente.
- Cada columna corresponde a un producto cuyo valor es el coeficiente que multiplica a dicho producto en la desigualdad.
- Hay una columna adicional que corresponde al término independiente de la regla.
En caso de tener reglas de tipo “mayor que”, éstas deben ser previamente giradas para convertirse de tipo “menor que” antes de crear la matriz de restricciones.
Las reglas de igualdad se deben tratar como dos reglas de desigualdad, una de tipo “menor que” y otra de tipo “mayor que”, donde esta segunda deberá ser transformada a tipo “menor que” antes de construir la matriz de restricciones.
Se entenderá mucho mejor si trabajamos con ejemplos mencionados anteriormente:
- Regla absoluta con importancia 0 que aplica día 2024-06-30.
- Matemáticamente, puede expresarse como 80 <= A <= 100.
- Si lo separamos en dos desigualdades obtenemos A > 80 y A <= 100.
- Si expresamos las dos desigualdades en formato “menor que” dejando el término independiente a la derecha de la desigualdad obtenemos -A <= -80 y A <= 100.
- Creamos la matriz de restricciones usando los coeficientes de las dos desigualdades anteriores, donde cada fila corresponde a una desigualdad:
| A | B | Independiente |
|---|---|---|
| -1 | 0 | -80 |
| 1 | 0 | 100 |
- Regla relativa con importancia 4 que aplica a día 2024-07-01.
- Matemáticamente, puede expresarse como 0.9 * B <= A <= 0.95 * B
- Si lo separamos en dos desigualdades obtenemos A > 0.9 * B y A <= 0.95 * B.
- Si expresamos las dos desigualdades en formato “menor que” dejando el término independiente a la derecha de la desigualdad obtenemos -A + 0.9 * B <= 0 y A – 0.95 * B <= 0.
- Creamos la matriz de restricciones usando los coeficientes de las dos desigualdades anteriores, donde cada fila corresponde a una desigualdad:
| A | B | Independiente |
|---|---|---|
| -1 | 0.9 | 0 |
| 1 | 0.95 | 0 |
Matriz de restricciones de reglas absolutas
El siguiente código convierte el objeto que contiene las reglas absolutas que aplican por día de interés a matriz de restricciones:
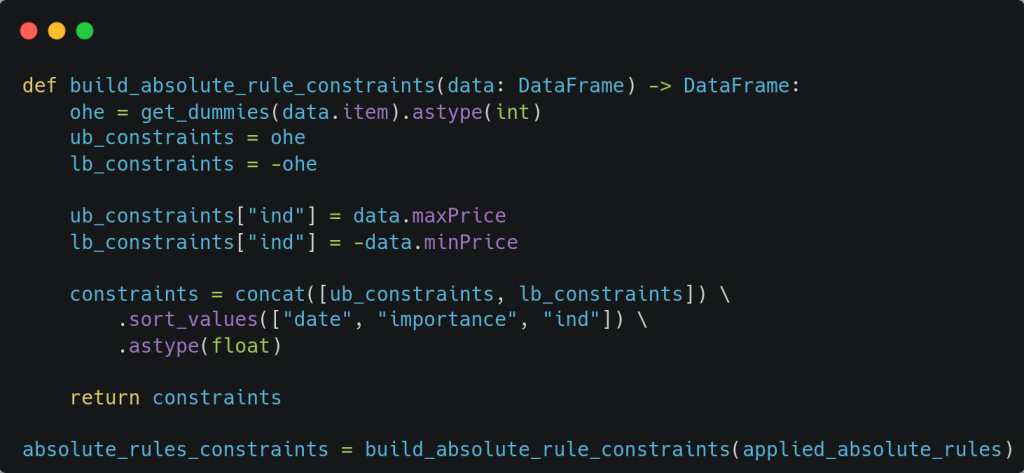
El resultado es el siguiente:
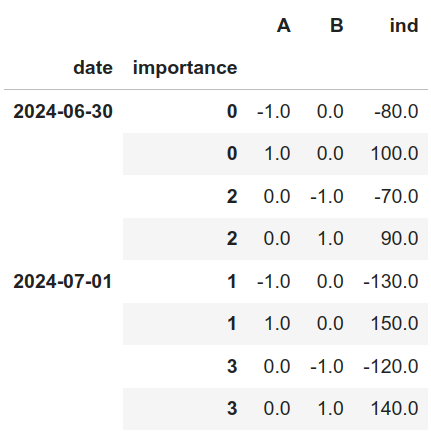
Matriz de restricciones de reglas relativas
De la misma manera, el siguiente código convierte el objeto que contiene las reglas relativas que aplican por día de interés a matriz de restricciones:
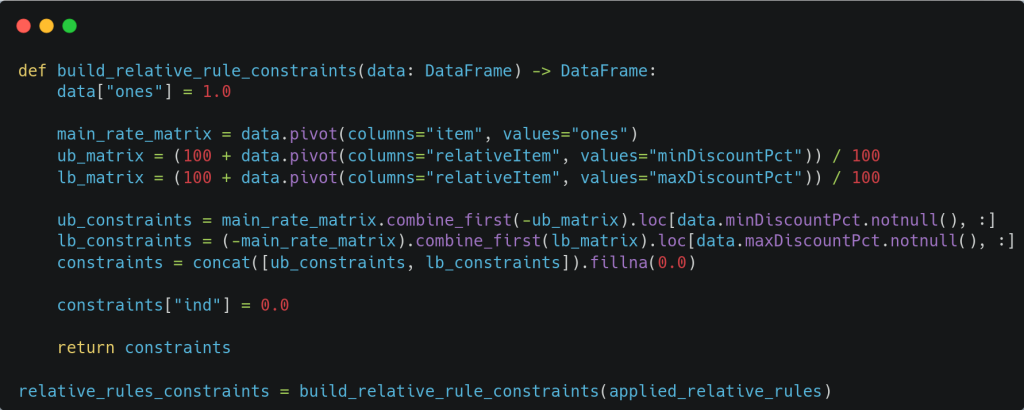
El resultado es el siguiente:
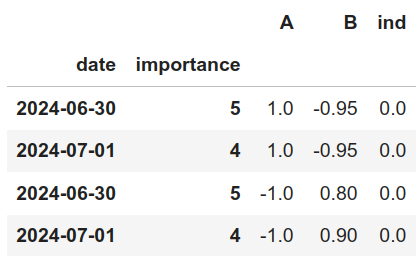
Matriz de restricciones completa
La matriz de restricciones completa no es más que la concatenación de las dos matrices de restricciones calculadas hasta el momento:
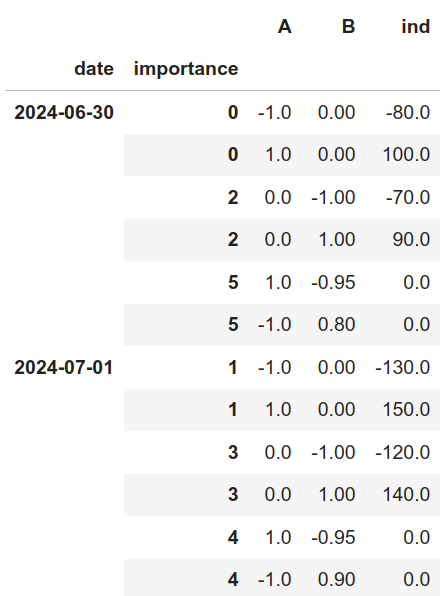
Reglas factibles
Una vez tenemos la matriz de restricciones calculada, ha llegado el momento de identificar qué restricciones no son factibles, es decir, que no se pueden aplicar si se quieren aplicar las que tienen mayor importancia debido a incompatibilidad.
Para resolver este problema, podemos usar programación lineal, el cual es un procedimiento matemático para optimizar funciones objetivo lineales con restricciones de desigualdad también lineales.
En nuestro contexto, no tenemos una función objetivo que queramos optimizar. Solo nos interesa saber si las restricciones permiten que exista una solución en caso que existiera una función objetivo.
El siguiente código analiza, por día de interés, cada una de las restricciones calculadas y determina si son o no factibles. En caso de no serlo, son descartadas. Esta función devuelve una matriz de restricciones que es factible.
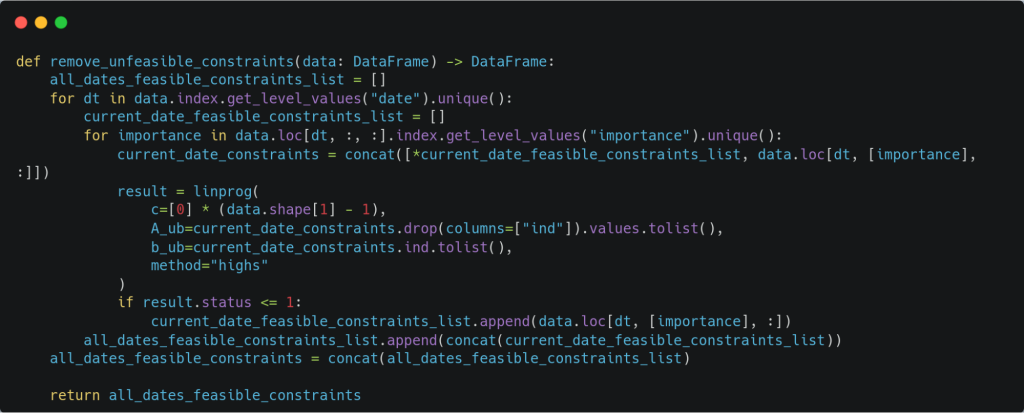
Dado que las reglas que hemos usado hasta el momento no generan conflicto entre ellas, todas las restricciones son factibles, por lo que el output de la función es el mismo que su input en el ejemplo que hemos estado trabajando, el cual es el siguiente:
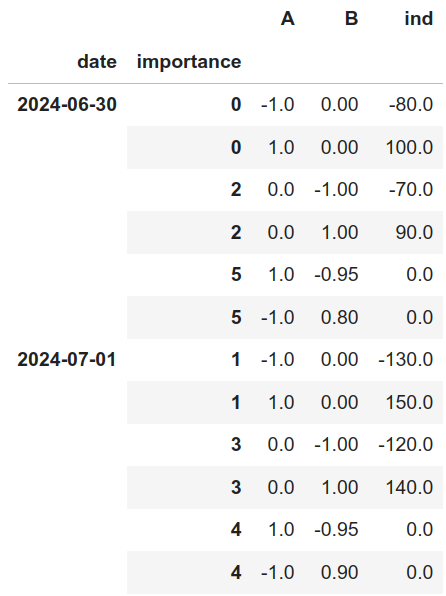
Caso con regla no factible
En este ejemplo, añadimos una regla absoluta que es incoherente con las anteriores y con un nivel de importancia menor (tiene menos prioridad). Dicha regla especifica que los lunes el producto A debe costar entre 800 y 1000. Esta regla es incoherente con la regla que especifica que los lunes el producto A debe costar entre 130 y 150. Por este motivo, la nueva regla que se ha añadido en este ejemplo debe ser descartada por el sistema.
En este nuevo contexto, las reglas absolutas que aplicar por cada día de interés son las siguientes:
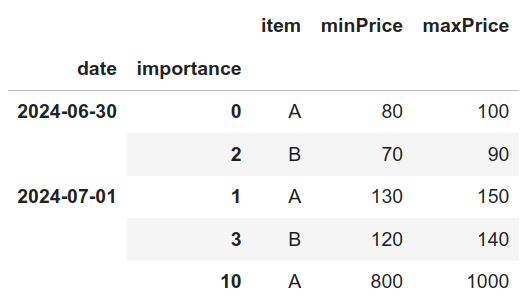
Se puede observar que se ha añadido una nueva fila con la importancia 10.
La nueva matriz de restricciones por tanto es la siguiente:
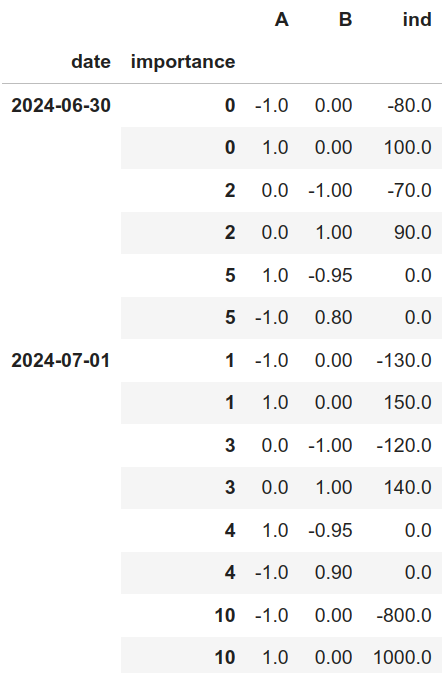
Si aplicamos de nuevo la función para eliminar reglas no factibles:
Se observará que devuelve el mismo resultado que cuando no existía esta nueva regla, lo cual implica que el sistema, de forma correcta, la ha descartado.
Conclusión
En este artículo hemos aprendido cómo resolver sistemas de reglas que determinan cuáles son los rangos de precios factibles por día y producto de interés. Mediante el uso de la técnica matemática Programación Lineal se han detectado qué reglas no permiten una solución del sistema.
Una limitación de esta metodología es que no aplica para contextos en los que las reglas generan restricciones que no son lineales. En la práctica esta limitación no es frecuente, ya que una necesidad de negocio común es que las reglas de precios sean fáciles de interpretar, por lo que mantener que sean lineales facilita su interpretabilidad.
