Muchas veces los conjuntos de datos que disponemos contienen un número de variables alto y lo que buscamos es poder explicar la relación entre las variables. Podemos realizar una reducción de la dimensionalidad del conjunto de datos consiguiendo un número menor de variables que expliquen la mayor cantidad de información posible de los datos originales, y aquí es donde entra en juego el Análisis de Componentes Principales (PCA, por su traducción al inglés).
PCA es un método matemático que pertenece a los métodos de aprendizaje no supervisado (no tenemos una variable target con etiquetas) y una de sus funciones es extraer información útil a partir de las variables originales. Esto nos ayuda a simplificar análisis posteriores como la representación de los datos en dos o tres dimensiones.
La idea matemática detrás es conseguir p variables ortogonales nuevas (componentes principales) y cada una de ellas es una combinación lineal de las m variables originales, de forma que expliquen la mayor cantidad de variabilidad del conjunto de datos original posible.
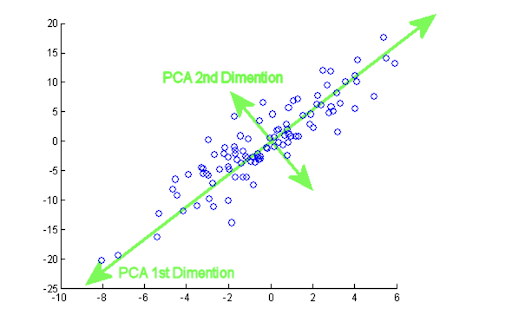
A continuación vamos a introducir la definición de valor y vector propios para la posterior explicación del PCA.
Valor y vector propios
Definamos A como una matriz de dimensión mxm y v un vector de dimensión 1xm no nulo, diremos que v es un vector propio de A si existe un escalar c tal que:
y c recibe el nombre de valor propio asociado al vector propio v.
Una forma de calcular los valores propios de la matriz A es empleando polinomios característicos. De la expresión anterior obtenemos que v(A-cI) = 0, entonces es equivalente a que det(A-cI) = 0. Los ceros de este polinomio son los valores propios de la matriz A.
Posteriormente, cuando realicemos la explicación del PCA, veremos que cada componente principal es un vector propio de la matriz de covarianzas y la varianza explicada de los datos originales por cada componente principal es el valor propio asociado al vector propio en cuestión.
Procedimiento del PCA
Una vez que tenemos la idea intuitiva de cómo funciona y cuál es el objetivo del PCA, además de definir los conceptos de valor y vector propios, es hora de mostrar los pasos para el cálculo de los componentes principales.
Dado un conjunto de datos X con n observaciones y p variables, queremos que haya un orden a la hora de conseguir los componentes principales de manera que el primer componente recoja la mayor varianza posible de los datos originales, el segundo componente recoge la mayor varianza no recogida por el primero, y así de forma sucesiva con los otros componentes.
Como estamos tratando de recoger la mayor varianza posible, las variables que tengan una magnitud mayor que otras tendrán mayor escala de varianza y, por tanto, dominarían sobre las otras variables. Para arreglarlo, primero tendremos que ajustar las variables originales de forma que tengan una magnitud comparable entre ellas, evitando así el problema anterior.
Estandarización
Hay diferentes maneras de transformar las variables para que estén en las mismas unidades, pero a nosotros nos interesa en particular estandarizar restando cada variable por su media, para después dividir este diferencia por su desviación típica:
Cálculo de los componentes principales
Recordemos que los componentes principales que estamos buscando son combinaciones lineales normalizadas de las p variables originales, y como mucho podemos tener min{n-1, p} componentes principales. Supongamos que queremos construir m componentes principales, entonces cada uno de ellos tendría el siguiente aspecto:
como se tratan de combinaciones lineales normalizadas, los vectores de coeficientes de los componentes principales son unitarios o normalizados y, por tanto, tienen módulo 1. Esta condición se refleja en la siguiente restricción:
Las α1j,…,αpj son las cargas o loadings del m-ésimo componente principal y cada una de ellas marca el peso que tiene cada una de las p variables en el componente y nos ayuda a recoger qué tipo de información recoge cada componente principal.
Teniendo todas las variables estandarizadas, podemos calcular el primer componente. De forma teórica, se trata de encontrar las α11,…,αp1 de forma que maximice la varianza del primer componente principal:
El símbolo ∑ denota la matriz de covarianza de X. Esta es la función que queremos maximizar y α11,…,αp1 las variables y la restricción es que:
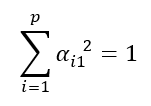
La formulación del problema de optimización es la siguiente:
Aplicamos el método de multiplicadores de Lagrange y nuestra función a maximizar es:
Derivamos la función F respecto de las α11,…,αp1 y con unas pocas manipulaciones algebraicas tenemos el sistema de ecuaciones siguiente en su forma matricial:
Para conseguir una solución no trivial del problema, α1 no nulo y obligatoriamente es la otra parte la que tiene que ser cero. Como explicamos en el apartado de Valor y Vector propios, nos damos cuenta de que la λ es un valor propio de ∑ con vector propio asociado α1. Calculamos la expresión del polinomio característico de la matriz de covarianza y habrá p valores propios asociados: λ1, λ2,…,λp. El valor propio que tenga un valor más grande será nuestra solución, ya que las λ representan la varianza del primer componente principal. Una vez escogido el valor propio, se procede a calcular el vector propio asociado (α1), pero lo obviaremos para no extender demasiado el post.
El cálculo de los componentes principales se realiza de forma semejante pero añadiendo las restricciones de no correlación pertinentes, ya que los componentes principales son ortogonales. Un resultado importante es que la suma de las varianzas de los componentes principales es igual a la suma de las varianzas de las variables originales, con lo cual:
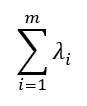
es la variación total del conjunto de datos original y la variación explicada por la j-ésima componente principal es:
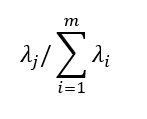
Conclusión
Este post es una introducción al Análisis de Componentes Principales y hemos dado una explicación breve de la base matemática que hay detrás del método. Al final, para conseguir los componentes principales, tenemos que resolver unos problemas de optimización con las restricciones de ortogonalidad y normalidad de los componentes principales.
Próximamente
En un post futuro ilustraremos un pequeño ejemplo de uso del PCA. Implementaremos en Python un ejemplo sencillo donde veremos el código empleado y algunos gráficos. En especial, veremos cómo podemos interpretar las variables originales en los ejes de los dos primeros componentes principales.
Mientras tanto, puedes pasarte por la categoría Algoritmos de nuestro blog y ver más artículos similares a este.

