La regresión es una metodología estadística que describe las relaciones entre una variable explicada continua y un conjunto de variables explicativas. En otras palabras, los modelos de regresión son capaces de predecir el valor de una variable dependiente y respecto a un conjunto de 
variables independientes 
.
La regresión lineal es un modelo de regresión donde se establece que la relación que se quiere explicar es lineal. Esta característica permite que los modelos sean fáciles de interpretar, pero a la vez puede ser restrictivo cuando las relaciones son más complejas. El modelo de regresión lineal poblacional se define como:
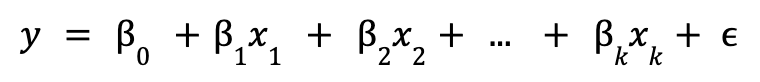
donde 
es la intersección, 
son los parámetros del modelo y 
es el término de error no observable, que representa los factores distintos a 
que afectan a 
.
Cuándo usar regresiones lineales
Se debería usar el modelo de regresión lineal cuando se busque crear un modelo simple y rápido, ya que no se necesita ajustar ningún hiperparámetro. Parte de la simplicidad del modelo se la lleva la linealidad de los términos. Esto puede parecer una gran restricción, pero en realidad la linealidad solo debe existir entre la variable dependiente 
y los parámetros del modelo 
, no con las variables independientes 
.
Esto quiere decir que variables independientes como las siguientes podrían ser válidas para construir el modelo.
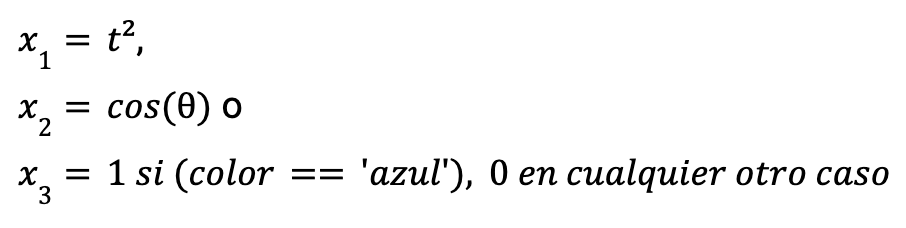
También es recomendable usar una regresión lineal cuando se priorice la interpretabilidad por encima del rendimiento o los resultados, ya que cada parámetro del modelo permite entender cuál es el peso o el efecto de la variable en cuestión sobre la variable explicada manteniendo el resto de variables explicativas constantes.
En cuanto a las variables, se espera que la variable explicada sea numérica. Si la variable dependiente es categórica en vez de numérica, habría que buscar un modelo de clasificación, como un árbol de decisión. Si la variable dependiente es categórica binaria, se puede usar una regresión logística para modelar la probabilidad de una categoría.
Adicionalmente, las variables explicativas no deberían mostrar una multicolinealidad alta, es decir, éstas no deberían poder expresarse como combinación de otras variables usadas en el modelo.
Método de mínimos cuadrados ordinarios
Una vez establecido el modelo de regresión lineal poblacional, se necesita una metodología para obtener sus parámetros. No obstante, normalmente no se tienen datos de toda una población, sino de una muestra de datos reducida. En consecuencia, se deben obtener estimaciones de estos parámetros a partir de la muestra y ver si se aproximan a los parámetros poblacionales. La rama de la estadística que se dedica a extraer conclusiones de propiedades de la población a partir de una muestra se llama estadística inferencial.
El método de mínimos cuadrados ordinarios (en inglés, Ordinary Least Squares o OLS) establece que los mejores estimadores para los parámetros de la regresión lineal son aquellos que minimizan la suma de los cuadrados de los residuos. Los residuos se definen como la diferencia entre el valor real de la variable explicada y el valor predicho por el modelo:
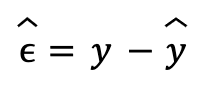
El resultado de esta minimización nos permite llegar a una solución matemática para los estimadores de los parámetros sin necesidad de usar optimización numérica, es decir, los estimadores se pueden calcular con fórmulas a partir de los datos. Esto no necesariamente ocurre con otras funciones de minimización de los residuos. La fórmula resultante en forma matricial es:
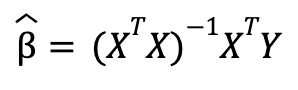
donde la matriz de variables independientes 
tiene dimensiones de k+1 (k variables y el término constante) y m observaciones, el vector de variables dependientes Y tiene dimensiones de m observaciones y los estimadores de los parámetros de la regresión lineal 
tienen dimensiones de k+1 variables (k variables y el término constante). El mismo resultado se puede obtener de suponer que el término de error no observable tiene media cero y no está correlacionado con las variables explicativas.
Interpretación de los resultados
El método de mínimos cuadrados ordinarios proporciona una manera de obtener estimadores de los parámetros para un modelo de regresión lineal. No obstante, se necesitan maneras para medir el rendimiento del modelo y sus predicciones y para poder compararlo con otros.
Una manera puede ser utilizar otra vez la suma del cuadrado de los residuos. Comparando esta métrica en dos modelos que predicen una misma variable explicada, se puede determinar cuál de los dos predice mejor el valor de la variable explicada escogiendo el que aporte menor error. En muchos casos, a esta métrica se le aplica una raíz cuadrada para mantener las mismas unidades que la variable explicada.
En otros casos, es más interesante tener una métrica que no tenga unidades. Este es el caso del coeficiente de determinación 
. Valores de este coeficiente cercanos a 1 implican que los valores predichos 
se aproximan al valor real , mientras que valores cercanos a 0 indican que poca variación del valor real es captada por la variación del valor predicho .
El resultado de las métricas vistas establece cómo de buenas son las predicciones del modelo. No obstante, por regla general, al añadir más variables explicativas al modelo, estas métricas muestran mejores resultados, sin importar si las variables son o no parte del modelo poblacional. Cuando se quiere determinar si el modelo creado a partir de los datos muestrales describe correctamente el modelo poblacional, hay que acudir a la estadística inferencial y a los tests de hipótesis.
En los tests de hipótesis, se establece una hipótesis nula 
sobre un parámetro de la población y se trata de contradecirla con los datos muestrales. A la práctica, se establece un umbral de probabilidad o nivel de significancia α y se calcula la probabilidad de obtener un valor del estimador muestral igual o más extremo data la hipótesis nula. Esta probabilidad se llama p-valor y cuando este es menor al nivel de significancia, se decide rechazar la hipótesis nula, asumiendo que rechazarla será erróneo en α% de los casos.
En el caso de la regresión lineal, se pueden realizar tests de
para determinar si, individualmente, los estimadores 
son estadísticamente significativos y afirmar que la variable 
es relevante para predecir , es decir, que 
es diferente de cero. De manera similar, se pueden realizar tests de 
para determinar si, conjuntamente, varios o todos los parámetros son significativos.
Estos tests son útiles para determinar si algunas variables explicativas deberían descartarse, pese a poder aportar valor en la varianza explicada. Es decir, ayudan a evitar un sobre ajuste del modelo a los datos (overfitting). Por otro lado, cuando se omiten variables del modelo que sí son relevantes se produce un sesgo en el resto de estimadores (underfitting).
Ejemplos en Python
A continuación, se va a ver cómo crear modelos de regresión lineal en Python usando dos librerías distintas. En primer lugar, la librería Scikit-learn (sklearn) proporciona multitud de herramientas para crear, ajustar y evaluar modelos de machine learning. Proporciona multitud de modelos de regresión, clasificación, clustering, etc. Entre las herramientas que incluye esta librería, se encuentran métodos para preprocesar datos, herramientas para seleccionar el mejor modelo y facilitar el ajuste de hiperparámetros o la reducción de la dimensionalidad de los datos de entrada.
Utilizar la librería de Scikit-learn es muy sencillo, ya que el uso de muchas de sus herramientas siguen un mismo esquema: se instancia la clase que se necesita (por ejemplo, un modelo) estableciendo unos parámetros, se ajusta a los datos usando el método fit() y, finalmente, se ejecuta el ajuste sobre unos datos usando predict() o transform() según si se ha ajustado un modelo o se quiere realizar una transformación. Los parámetros del modelo se pueden encontrar en los atributos de este una vez se ha ajustado.
En el siguiente ejemplo, se crea un modelo de regresión lineal en Scikit-learn para unos datos previamente generados, que se componen de 3 variables explicativas y una variable explicada, con un total de 30 registros. En primer lugar, se cargan los datos en un DataFrame de la librería pandas.
import pandas as pd
df = pd.read_csv('data.csv')
print(f"Filas: {df.shape[0]}")
print(f"Columnas: {df.shape[1]}")
df.head(5)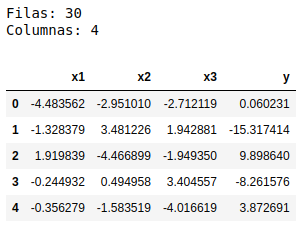
Seguidamente, se usa la clase LinearRegression para crear y ajustar el modelo de regresión lineal. Se muestran los estimadores de los parámetros de la regresión accediendo a los atributos intercept_ y coef_ del modelo ajustado.
from sklearn.linear_model import LinearRegression
X = df[['x1','x2','x3']]
Y = df.y
lr = LinearRegression()
lr.fit(X, Y)
print(f'b0 = {lr.intercept_:7.4f}')
print(f'b1 = {lr.coef_[0]:7.4f}')
print(f'b2 = {lr.coef_[1]:7.4f}')
print(f'b3 = {lr.coef_[2]:7.4f}')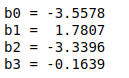
Finalmente, se evalúa el modelo usando diferentes métricas de sklearn.metrics. Se obtiene un valor del coeficiente de determinación alto. Eso implica que las predicciones obtenidas se ajustan bastante bien a los valores reales.
from sklearn.metrics import mean_squared_error, r2_score
Y_pred = lr.predict(X)
print(f"MSE = {mean_squared_error(Y, Y_pred):6.3f}")
print(f"RMSE = {mean_squared_error(Y, Y_pred, squared=False):6.3f}")
print(f"R2 = {r2_score(Y, Y_pred):6.3f}")
Por otro lado, la librería Statsmodels proporciona multitud de modelos y tests estadísticos en los que probar los datos. Para ajustar una regresión lineal, se usa la clase OLS. Después de ajustar los datos con el método fit(), se pueden mostrar los resultados de manera muy detallada usando summary(). A continuación, se realiza un ajuste con esta librería usando los mismos datos que antes.
import statsmodels.api as sm
X = df[['x1','x2','x3']]
Y = df.y
# Se añade una variable constante de 1 (b0*1)
X = sm.add_constant(X)
ols = sm.OLS(Y, X)
results = ols.fit()
results.summary()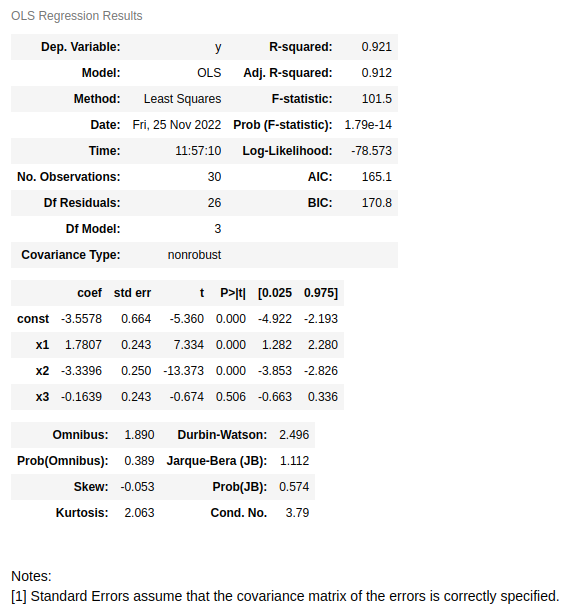
En la primera tabla de los resultados se puede ver que se recupera el mismo valor de y en la segunda tabla se puede ver que los estimadores también coinciden. Adicionalmente, en la tabla de arriba también se representa el valor del estadístico y el p-valor del test de . En este caso, este test establece como hipótesis nula que todos parámetros usados en la regresión son cero y que no ayudan a explicar la variable dependiente. El valor resultante es muy pequeño y, por tanto, la hipótesis nula se rechaza, es decir, hay alguna variable escogida en el modelo que sí tiene peso para explicar .
Por otro lado, en la segunda tabla, a la derecha de los valores de los estimadores, se muestra el error asociado a cada uno, el valor del estadístico , el p-valor obtenido de realizar el test dey el intervalo de confianza de cada estimador del 95% (α = 5%). Se observa que el p-valor para la variable
es alto, comparado con el umbral de probabilidad típico (5%). Esto significa que no se puede afirmar que 
no sea cero. Es decir, en la muestra no hay suficiente evidencia estadística para rechazar la hipótesis nula del test derealizado sobre este parámetro. Por tanto, podría ser conveniente no usarlo en el modelo.
Conclusión
En conclusión, la regresión lineal es un modelo sencillo que permite explicar los valores de una variable numérica como una combinación lineal de diferentes variables explicativas. El método de los mínimos cuadrados ordinarios permite estimar los parámetros de la población, que se pueden interpretar como el peso de la variable independiente sobre la variable dependiente. Se pueden realizar tests sobre estos estimadores para entender si el modelo creado a partir de una muestra es adecuado para explicar la población.
Para acabar, se han explorado dos posibilidades para implementar la regresión lineal en Python. Se han usado las librerías Scikit-learn y statsmodels. La primera está orientada a machine learning, con multitud de herramientas y modelos para tratar los datos, mientras que la segunda está orientada a estadística, con diferentes tests de hipótesis en los que probar los datos.
