Una regresión lineal es un modelo que se usa para aproximar la relación lineal entre una variable dependiente Y y un conjunto de variables independientes X. En formato matricial puede expresarse como
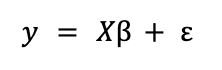
donde ε es un vector de términos aleatorios o errores. β es el de los parámetros a estimar, un proceso que se lleva a cabo resolviendo un problema de optimización en el que el objetivo es minimizar el error cuadrático medio (MSE). Es decir, aplicando el método de mínimos cuadrados ordinarios (OLS).
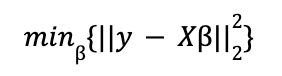
Para una visión más en profundidad sobre la regresión lineal, léase el post sobre Regresión Lineal con Python en nuestro blog.
OLS es un método que no ha perdido vigencia desde que Gauss empezó a usarlo a principios del siglo XIX, aunque, como señalan Hasties, Tibshirani & Wainwright (2015) existen dos razones por las que cabría considerar alternativas:
- La precisión de la predicción puede mejorarse a veces disminuyendo el valor de los coeficientes de la regresión. En este sentido, reducir el valor de los estimadores aumenta el sesgo pero reduce la varianza en los valores a predecir.
- De acuerdo con el primer punto, los coeficientes pueden llegar a reducirse a cero, seleccionando variables de manera indirecta. En un modelo con un gran número de variables explicativas al inicio, mejora su interpretabilidad.
Lasso y Ridge son dos métodos que combinan la minimización del error cuadrático medio de OLS con el establecimiento de límites o penalizaciones a los coeficientes.
Definición de las penalizaciones L1 y L2
Lasso (L1) penaliza la suma del valor absoluto de los coeficientes. En este caso, la función de minimización en forma lagrangiana tendría la forma
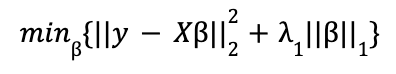
Ridge (L2) penaliza la suma del cuadrado de los coeficientes. La función de minimización en forma lagrangiana es:
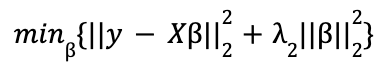
donde, en cada caso, λ representa el parámetro de ajuste con valor 
.
La combinación de ambas penalizaciones es la expresión de una Red Elástica:
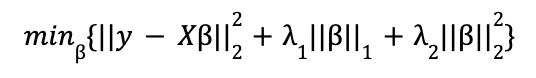
Si bien formalmente, y también en las implementaciones de Scikit-Learn y Statsmodels, la expresión que se minimiza es ligeramente distinta:
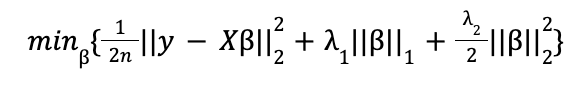
donde n es el tamaño muestral.
Respecto de las penalizaciones L1 y L2, cabe señalar que:
- Comparado con la solución OLS, ambos métodos reducen el valor de los coeficientes, pero solo la penalización L1 puede hacer que algunos sean cero. Con lo cual, L2 no sirve para hacer selección de variables de manera automática.
- Si existen variables muy correlacionadas, con L1 se podría escoger aleatoriamente una de ellas y establecer la otra como cero.
- Como L2 no anula coeficientes, los que devuelve están mejor distribuidos. En algunos casos puede resultar preferible a L1 si el modelo no tiene muchas variables explicativas y se tiene la certeza de que todas ellas deben estar en él.
- En ambos casos, distintos valores de pueden asociarse con distintos niveles de sesgo y varianza. El punto óptimo en el trade off entre estas dos medidas es el que minimizaría el Error Cuadrático Medio (MSE).
- En todo caso, como a priori ambos métodos consideran los coeficientes conjuntamente, es importante re-escalar las variables antes de correr la regresión. De lo contrario se estarían regularizando con el mismo criterio coeficientes de variables en rangos distintos.
En adelante se analizan las implementaciones en Python para Red Elástica, cuyos casos extremos incluyen las regresiones Ridge y Lasso.
Regresión lineal con red elástica en Python
A modo de ejemplo, se usará el paquete load_diabetes de sklearn.datasets, dividido en datos de entrenamiento y test.
Los datos ya vienen normalizados.
Scikit-Learn
En scikit-learn, pueden efectuarse regresiones lineales con red elástica con las clases ElasticNet y ElasticNetCV. La regularización se aplica con los parámetros alpha(s) y l1_ratio pasados a la clase. alpha(s) es el valor que representa la severidad conjunta del parámetro de ajuste; l1_ratio es un valor entre 0 y 1 que representa la proporción de L1 sobre el total de la penalización. ElasticNetCV admite vectores para alphas y l1_ratio y el mejor modelo se selecciona de manera automática.
Nótese, sin embargo, que los valores en alphas y l1_ratio no se corresponden con las penalizaciones λ1 y λ2 de la red elástica como se define en la ecuación 6. Tal como la propia documentación del paquete señala en la clase ElasticNet, si quisieran controlarse las penalizaciones de manera independiente, cabría considerar que, para cada combinación de valores en alphas y l1_ratio:
alpha = λ1 + λ2
l1_ratio = λ1 / (λ1 + λ2)
Con lo cual, con valores dados de λ1 y λ2, deberían traducirse los valores en alphas y l1_ratio antes de pasarlos a ElasticNetCV.
Algunos parámetros útiles con los que probar alternativas incluyen fit_intercept=False y positive=True que, respectivamente, pueden servir para correr regresiones sin intercepto o forzando un valor positivo en todos los coeficientes.
Implementación de Statsmodels
En Statsmodels, la regularización se aplica con los parámetros alpha y L1_wt dentro del método .fit_regularized. Como con scikit-learn, para Redes Elásticas, la penalización alpha se reparte entre ambas regularizaciones dependiendo del valor de L1_wt, equivalente a l1_ratio en scikit-learn.
Statsmodels no permite hacer directamente validación cruzada. Aunque sería posible aplicarla con un desarrollo más a fondo, se obvia porque escapa al alcance que se pretende aquí. En Statsmodels, probar distintos valores de alpha y L1_wt requiere correr regresiones en bucle para escoger la mejor combinación.
Representando la matriz de valores alpha – L1_wt en un mapa de calor:
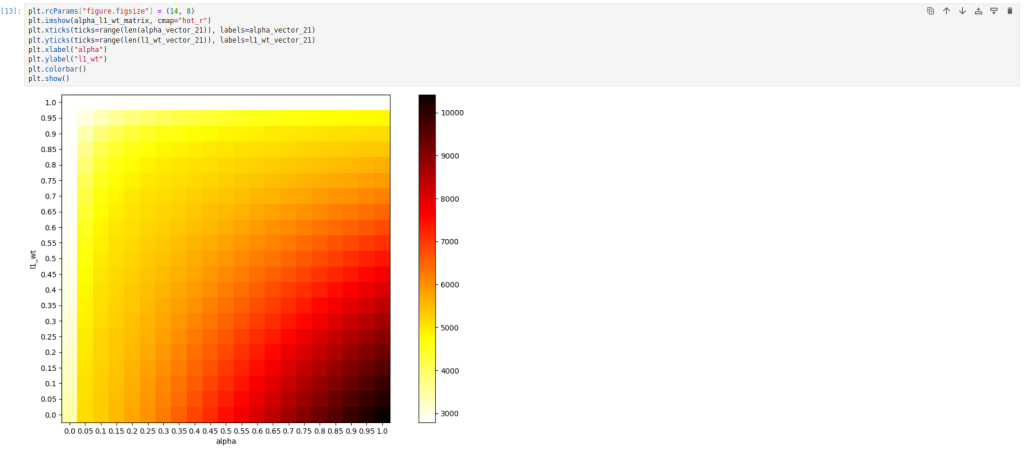
La falta de una implementación propia que se sirva de validación cruzada o que admita los parámetros en vectores como en ElasticNetCV de scikit-learn podría llevar a la conclusión que una implementación de Statsmodels es más verbosa o más limitada. Sin embargo, Statsmodels tiene ventaja sobre scikit-learn en la flexibilidad del manejo de las penalizaciones para casos en que deseen aplicarse en magnitudes variables en los distintos coeficientes del modelo. Para ello, es necesario pasar al parámetro alpha un vector de penalizaciones de longitud igual al número de variables. Un caso de uso podría ser el de aplicar sólo penalizaciones a algunos coeficientes del modelo y no a todos. Por ejemplo, en caso de no querer imponer ningún tipo de penalización a la variable “s1”, en posición 5, podría repetirse el ejercicio anterior imponiendo que alpha sea 0 en la posición 5, iterando un valor constante sobre el resto:
Con la posibilidad de otorgar distintas penalizaciones por variable, se abre un abanico de dimensiones adicionales para eventualmente mejorar la capacidad predictiva de los modelos lineales. Pero, ¿es posible establecer algún criterio con el que escoger los pesos por variable, sin tener que probar las miles de posibles combinaciones? Respecto de este tema, Tay et al. (2023) proponen modificar los algoritmos para asignar una puntuación a las variables basándose en una matriz donde se representa la “información sobre los predictores” (variables de variables) en un método que llaman “feature-weight elastic net”, y cuya implementación en Python no existe a la fecha de publicación de esta entrada (aunque sí programaron un paquete en R).
Conclusión
La aplicación de las penalizaciones L1 y L2 son métodos que pueden mejorar la capacidad predictiva en las regresiones lineales, además de simplificar los modelos a través de una selección indirecta de variables. La regularización por redes elásticas permite aplicar simultáneamente ambos tipos de penalización.
En Python, las regresiones lineales con red elástica están implementadas en los paquetes Statsmodels y scikit-learn. Scikit-learn posee una implementación con validación cruzada muy cómoda de utilizar y Statsmodels, con la posibilidad de programarse a parte la validación cruzada, presenta una flexibilidad interesante respecto del manejo de las penalizaciones a nivel de variable. Sin embargo, la explotación de todas las posibilidades que puede ofrecer esta flexibilidad requeriría incrementar en varias magnitudes el número de iteraciones. Como alternativas al uso de fuerza bruta se han propuesto algunos algoritmos como el de Tay et al. (2023), aunque a día de hoy no existe implementación en Python.
Bibliografía
– Hastie, T., Tibshirani, R., & Wainwright, M. (2015). Statistical learning with sparsity: the lasso and generalizations. CRC press.
– Tay, J. K., Aghaeepour, N., Hastie, T., & Tibshirani, R. (2023). Feature-weighted elastic net: using «features of features» for better prediction. Statistica Sinica, 33(1), 259–279. https://doi.org/10.5705/ss.202020.0226.
