Programación Lineal y Método Simplex

Introducción

A todos nos suena el concepto de Programación Lineal u Optimización Lineal, aquella rama de las matemáticas que se dedica a optimizar (maximizar o minimizar) una función objetivo lineal sujeta a unas restricciones en forma de ecuaciones y/o inecuaciones. Aunque se trate de una rama avanzada de las matemáticas, su uso es extendido en la vida cotidiana como puede ser la gestión de la compra del mes intentando gastar el mínimo dinero posible pero cumpliendo una serie de requisitos.

En este post vamos a empezar por definir unas nociones básicas sobre la Programación Lineal y los diferentes tipos que hay para sentar unas bases sólidas, para después introducir el método Simplex, un algoritmo muy utilizado para resolver problemas de optimización lineal.

Nociones básicas

Como bien indica en el nombre, en la programación lineal las funciones y las restricciones son lineales. Por tanto, función objetivo es una función de n variables lineal y las restricciones deben ser ecuaciones o inecuaciones lineales.

Una definición general de un problema de optimización de programación lineal es:

¿Qué es lo que realmente queremos obtener como solución? La solución es un vector n dimensional en el que se cumplen todas las restricciones del problema y optimice la función objetivo. Puede haber muchos vectores que cumplan las restricciones y los denominamos solución factible. Veamos un ejemplo para poder ilustrar de forma más clara los dos conceptos:

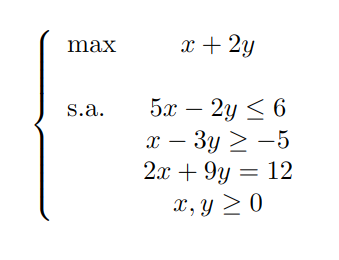
La región de las soluciones factibles en este caso sería: {(x,y)R²:5 x-2y<=6, x-3y>=-5, 2x+9y=12, (x,y)>=(0,0)}.

Como vemos, las restricciones que aparecen pueden ser de tipo desigualdad y de igualdad, pero para emplear el algoritmo Simplex necesitamos que las restricciones sean todas de igualdad (aunque la implementación que veremos después es flexible y no exige tal condición), además de otras condiciones que mencionaremos en breve. Para ello, vamos a introducir otra forma de expresar un problema de optimización y es la Forma estándar de un Problema de Optimización de Programación Lineal:

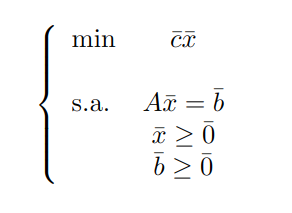
El objetivo es poder transformar cualquier tipo de problema de optimización a su forma estándar. Para ello necesitamos una manera de realizar esta transformación y la metodología que permite esto consiste en los siguientes pasos:

1. Si el problema es de maximizar la función objetivo 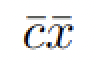, debemos cambiar a minimizar .
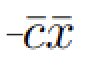2. Si existe algún término independiente de las restricciones de igualdad negativo, cambiamos el signo a toda la restricción.
3. Las restricciones de desigualdad pueden convertirse en restricciones de igualdad introduciendo las denominadas variables de holgura:
   • Si tenemos a_i1x₁ +...+ a_inx_n <= b_i, podemos transformarla utilizando una variable x_hi >= 0 así: a_i1x₁ +...+ a_inx_n + x_hi = b_i.
   • Si tenemos a_i1x₁ +...+ a_inx_n >= b_i, podemos transformarla utilizando una variable x_hi >=0 así: a_i1x₁ +...+ a_inx_n - x_hi = b_i.
4. Si alguna variable de decisión x_i no cumple con la condición de no negatividad no se cumple, entonces la sustituimos por 2 nuevas variables y_i, z_i tal que x_i = y_i + z_i.

Veamos un ejemplo de cómo pasar un problema de optimización a su forma estándar:

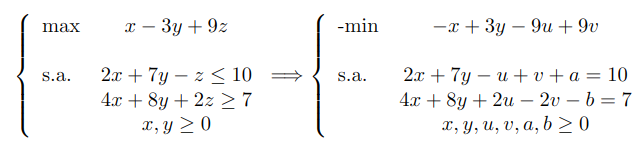
Método Simplex

Consideraremos solamente los problemas en su forma estándar para el método Simplex. Para ello, hay un concepto importante que es solución factible básica.

Solución Factible Básica

Consideremos un problema de optimización en su forma estándar. Vamos a fijar algunos conceptos que son necesarios para definir una solución factible básica, siendo A la matriz de coeficientes de las restricciones de igualdad de dimensión mxn:

1. Matriz Básica: Una submatriz B cuadrada (mismo número de filas y columnas) no singular (existe su inversa) de A de dimensión m se denomina matriz básica. Además, B es una matriz básica factible si
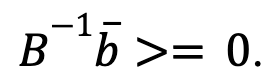
2. Llamaremos N a la submatriz de A con dimensión mx(n-m) que tiene como columnas las de A que no están en B.
3. Sea 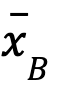el vector de variables de decisión asociadas a las columnas de la matriz A necesarias para construir B. Se denominan variables básicas.
4. Sea 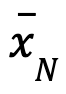el vector de variables de decisión asociadas a las columnas de la matriz A necesarias para construir N. Se denominan variables no básicas.
5. Si exigimos que 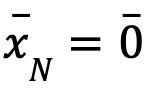tendríamos:

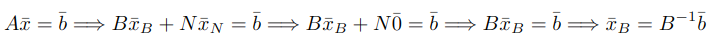
Teniendo en cuenta lo expuesto, la solución del sistema de ecuaciones se le denomina solución factible básica si .

Procedimiento

Vamos primero a fijar la notación necesaria para explicar el procedimiento.

• Sea B una submatriz cuadrada no singular de dimensión m de A. Entonces denotaremos por I y J los conjuntos con los índices asociados a las columnas de B y N, respectivamente.
• Sea 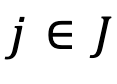y 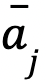la columna j-ésima de A, denotamos el vect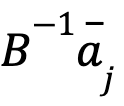or por .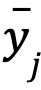
• Sea 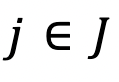y 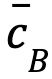es el vector formado por los coeficientes de la función objetivo asociados a las columnas de la submatriz B, denotamos por z_j el valor .

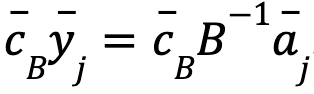El método Simplex se dedica a buscar todas las soluciones factibles básicas una a una y verificar si son óptimas o no. Lo hace de forma iterativa hasta encontrar la solución factible básica óptima o hasta verificar que el problema no tiene solución. 

Supongamos que es una solución factible básica, entonces se realizan los siguientes pasos:

1. Si existe 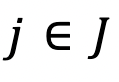tal qu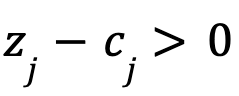e e 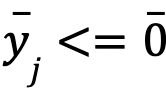, entonces el problema de optimización en su forma estándar no admite solución óptima.
2. Si z_j - c_j <= 0, ∀j ∈ J, entonces 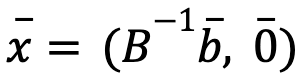es una solución factible óptima ↔ z_j - c_j <= 0, ∀j ∈ J. Si se cumple que max{z_j - c_j: j ∈ J} = 0 entonces el problema es factible pero la solución óptima no es única.
3. Si el Simplex no ha podido determinar ninguna decisión, se calcula una nueva solución factible básica y se vuelven a aplicar los pasos anteriores.

Método Simplex en Python

Una vez que hemos explicado los entresijos del método Simplex, veamos cómo emplearlo en Python. El módulo optimize de la librería SciPy contiene un método llamado linprog() para resolver problemas de optimización de programación lineal (visita la documentación oficial para más información). Cabe recordar que este método no nos exige que todas las restricciones sean de igualdad, también incluye la opción de incorporar restricciones de menor o igual.

Consideremos el siguiente problema de optimización:

En total hay 6 restricciones (2 de cada tipo) y 4 variables de decisión, resultando su resolución a mano un proceso muy costoso. La implementación en Python es la siguiente:

from scipy.optimize import linprog
import numpy as np

A_ub = np.array([[7, -23, 5, 9], [-5, 3, 1, 0], [-4, 8, -12, -4], [-3, -2, -9, -10], 
     [-1, 0, 0, 0], [0, -1, 0, 0], [0, 0, -1, 0], [0, 0, 0, -1]])
A_eq = np.array([[-16, 28, 5, 8], [0, -5, 3, 2]])
b_ub = np.array([56, 7, -1, -6, 0, 0, 0, 0])
b_eq = np.array([5, 8])
c = np.array([-4, 9, -1, 3])

linprog(c=c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, method="simplex")

El resultado que obtenemos es:

       con: array([ 5.68434189e-13, -2.84217094e-14])
       fun: -60.305084745761874
message: 'Optimization terminated successfully.'
       nit: 9
    slack: array([5.68434189e-13, 2.19237288e+02, 7.02389831e+02,           
               7.75508475e+02, 7.26101695e+01, 3.17457627e+01,   
               5.55762712e+01, 0.00000000e+00])
    status: 0
    success: True
          x: array([72.61016949, 31.74576271, 55.57627119,  0.        ])

El método ha finalizado con éxito en su búsqueda de la solución factible óptima en 9 iteraciones. La solución óptima que obtenemos es y el valor mínimo de la función objetivo  es -60.31.

Hasta aquí nuestro post de hoy. Si te ha parecido interesante, te animamos a visitar la categoría Algoritmos para ver todos los posts relacionados y a compartirlo en redes con tus contactos. ¡Hasta pronto!