Introducción
La gestión de ingresos (GR) puede definirse como un conjunto de técnicas centradas en el análisis del comportamiento de los consumidores con el fin de obtener el mayor beneficio posible. En general, es clave entender cómo responder a disposición de los clientes a comprar un determinado bien al precio de éste. De este modo, se puede estimar cómo afectará a la demanda un cambio en el precio, y así tomar medidas para maximizar los ingresos.
Centrándonos en el contexto hotelero, el problema de encontrar la relación entre el precio y la demanda puede resultar muy complicado, ya que entran en juego múltiples actores. Naturalmente, puede haber distintos tipos de clientes que respondan de forma diferente a las variaciones de precio. Por ejemplo, los clientes del ocio tienden a ser bastante flexibles al precio, lo que significa que una variación en el precio puede afectar sustancialmente a su disposición hacer una reserva. Esto contrasta con los clientes de negocios, que en general son menos flexibles en cuanto al precio, ya que a menudo se les reembolsan los gastos y, por tanto, no les importa reservar una habitación a una tarifa más alta.
Además de los diferentes tipos de clientes, también se podrán considerar diferentes tipos de habitaciones, con diferentes precios asociados. Por otro lado, podríamos encontrar un comportamiento diferente de los clientes según la temporada o el día de la semana, entre otros factores.
En este post, a efectos ilustrativos, nos ceñiremos a un escenario sencillo en el que nos consideramos diferentes tipos de clientes, temporadas o habitaciones. Nuestro propósito no es deducir el comportamiento de la demanda a partir de un conjunto de datos dados. En su lugar, definiremos a continuación un modelo simple de demanda, y nos centraremos en encontrar una estrategia de precios óptima dado este modelo.
Un modelo de demanda hotelera sencillo
Supongamos el siguiente escenario: somos el gestor de un hotel que necesita fijar los precios de las habitaciones con una antelación de hasta T días. Por ejemplo, T = 356 en el caso de que permitamos reservar hasta un año antes de la fecha de entrada. El precio para una fecha de estancia determinada se fija al principio de cada día de reserva y se mantiene durante todo el día.
Al principio del día siguiente podemos elegir un precio diferente para ir una fecha de llegada, y el mismo proceso se repite hasta la fecha de llegada, incluida. Imaginemos que nuestro objetivo es maximizar los beneficios totales obtenidos de las reservas de habitaciones al día siguiente de la llegada (ya que permitimos las reservas el mismo día). Naturalmente, para establecer una estrategia de precios, necesitamos tener algún conocimiento sobre cómo responderá el número de habitaciones demandadas para una fecha de estancia determinada, o la demanda, a un cambio de precio.
Un enfoque habitual en la literatura sobre la estimación de la demanda hotelera es considerar la demanda habitaciones como una variable aleatoria. Esta cantidad se considera como la combinación de las decisiones individuales de un número de clientes potenciales que buscan alojamiento en un mercado donde nuestro hotel tiene presencia. Este número de individuos que denominamos llegadas al mercado, o simplemente llegadas, se denota por 𝐴.
Consideremos una fecha de entrada fija para la que queremos maximizar los beneficios obtenidos de las reservas de habitaciones. En general, indicaremos las variables de nuestro modelo con 𝑡, que denota el número de días entre el día actual y la fecha de llegada. Supongamos que el número esperado de llegadas en el momento 𝑡 (es decir, 𝑡 días antes de la llegada), denotado por 𝐴𝑡 aumenta linealmente a medida que nos acerquemos al día de llegada (o 𝑡 se aproxima a cero). Consideremos que la distribución de probabilidad del número de llegadas 𝐴𝑡 en un determinado día 𝑡 de antelación viene dada por:
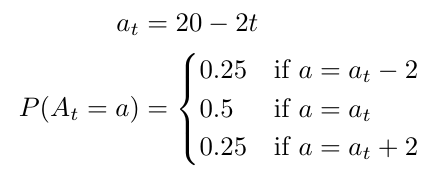
De lo contrario 𝑡 ∈ [0, 9] and 𝑃 (𝐴𝑡 = 0) = 1 . Esto significa que ningún cliente busca alojamiento en nuestro mercado antes de los 9 días previos a la llegada, y a partir de 𝑡 = 9 el número potencial de clientes aumenta linealmente. Por ejemplo, en 𝑡 = 9 tenemos un número esperado de llegadas 𝑎9 = 2 , por lo que hay un 25% de posibilidades de que tengamos 𝐴9 = 2 – 2 = 0 de nuevas llegadas al mercado, un 50% de posibilidades de que 𝐴9 = 2 sean nuevas llegadas, y un 25% de posibilidades de que tengamos 𝐴9 = 2 + 2 = 4 nuevas llegadas. En el día de llegada (𝑡 = 0), tenemos 𝑎0 = 20, por lo que los valores posibles de 𝐴0 son 18, 20 y 22, con probabilidades respectivas del 25%, 50% y 25%. Por supuesto, en general la función de llegada será mucho más compleja, pero como hemos dicho, este ejemplo está simplificado a efectos de ilustración. La figura 2 muestra el aspecto de la curva de llegada.
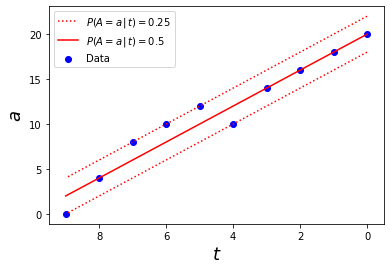
Una vez conocida la distribución de las llegadas (el número de clientes potenciales en nuestro mercado en un día determinado), calculemos la distribución de la demanda real. Parece seguro suponer que cada individuo toma su decisión independientemente del resto, y que elegirá si reserva o no una habitación en nuestro hotel en función de algún valor de utilidad. Por supuesto, estos valores de utilidad pueden variar entre segmentos de clientes, e incluso dentro de estos grupos, ya que cada persona tiene su propia concepción de la utilidad. De nuevo, por simplicidad, supongamos en este modelo que las probabilidades de que cada uno de los clientes potenciales elija nuestro hotel son iguales, y llamemos a este valor común la probabilidad de elección. Con este supuesto, la demanda sigue una distribución binómica, cuyo parámetro de tamaño es el número de y el parámetro de probabilidad es la probabilidad de elección.
La probabilidad de elección puede definirse formalmente de la siguiente manera. Sea 𝑋 una variable aleatoria de Bernoulli que toma los valores 1 o 0 en función de si un determinado cliente del mercado decide reservar una habitación en nuestro hotel o no, respectivamente. Entonces, la probabilidad de elección es simplemente la probabilidad de que 𝑋 sea igual a 1. Naturalmente, esta probabilidad depende del precio p que fijemos y ¡potencialmente de otros factores, como los precios de los competidores y otras cantidades, menos como la percepción del cliente sobre la calidad de los diferentes hoteles. Para este ejemplo consideremos la probabilidad de elección ingenua
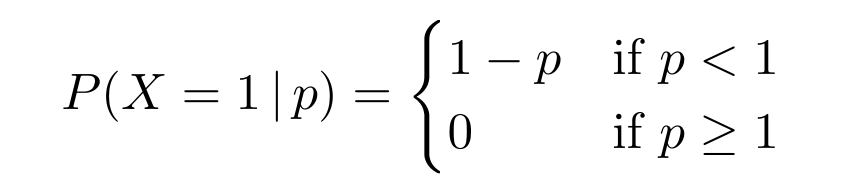
que fija un límite superior para el precio. En efecto, si 𝑝 ≥ 1 la probabilidad de elección es cero, lo que significa que nadie reserva una habitación en nuestro hotel, y a medida que 𝑝 se acerca a cero tenemos una mayor probabilidad de que nuestro hotel sea elegido.
Una vez que conocemos la probabilidad de elección común y el número de llegadas al mercado en el día actual 𝑡, el número de habitaciones demandadas 𝐷𝑡 se puede calcular como una binómica de la siguiente manera:
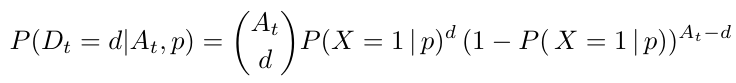
Sin embargo, en la práctica, el número de llegadas 𝐴 será desconocido, ya que debemos ser capaces de estimar la demanda en un determinado día 𝑡 antes de que éste llegue. Por ejemplo, podríamos obtener una demanda de 10 habitaciones en el día 𝑡 como resultado de la llegada de 20 clientes al mercado, de los cuales la mitad deciden reservar en nuestro hotel, o como resultado de la llegada total de 100 clientes con sólo una décima parte de la cuota de mercado. Ambos escenarios, con sus respectivas probabilidades, deben ser para calcular la probabilidad de la demanda.
Por tanto, tenemos que reescribir la expresión anterior teniendo en cuenta que el número de llegadas en función de 𝑡 es a su vez estocástico, con la distribución de probabilidad definida anteriormente. Así, la probabilidad de tener una demanda d en el día 𝑡 dado que fijamos un precio 𝑝 viene dada por
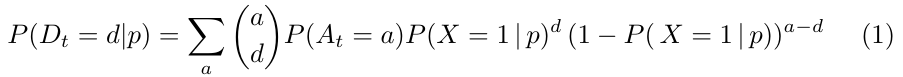
donde a abarca todos los valores posibles del número de clientes potenciales en el día 𝑡.
Ya conocemos la distribución del número de habitaciones demandadas en cualquier momento de antelación 𝑡 cuando se fija un precio 𝑝. Sin embargo, una característica distintiva del escenario de la demanda hotelera es que la cantidad de bienes suministrados, es decir, el número de habitaciones, está acotada 
. Por lo tanto, la demanda realizada 
(número de habitaciones realmente reservadas) podría no ser igual al número de habitaciones demandadas cuando no hay suficientes habitaciones disponibles.
En concreto, dejemos que 𝑛𝑡 sea la ocupación (número de habitaciones ya reservadas para una fecha de estancia determinada) al principio del día 𝑡, y que 𝑑𝑡 sea el número de habitaciones demandadas durante el día 𝑡. Siguiendo una política estricta de sobre reserva, en la que no permitimos exceso de capacidad, las expresiones para la demanda realizada 𝑑𝑡 y para la ocupación en del día siguiente 𝑛𝑡-1 vendrán dadas por
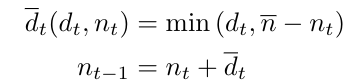
En otras palabras, permitiremos todas las reservas hasta alcanzar la capacidad total.
Cabe señalar que, en la mayoría de los escenarios del mundo real, los hoteles también permiten las cancelaciones por adelantado. Estas cancelaciones dejarían espacio para nuevas reservas, lo que modificaría ligeramente nuestro modelo. En concreto, si ct es el número de reservas canceladas en el día 𝑡, la demanda realizada pasaría a ser 
. Si las cancelaciones pudieran ser, también se podría permitir un determinado nivel de sobre reserva para garantizar la plena ocupación.
Siguiendo el principio de simplicidad, en este modelo no permitimos las cancelaciones ni el exceso de reservas. Sin embargo, podrían añadirse con poca sobrecarga.
Estrategia de precios óptima: la función de valor
Recordemos que hemos dicho que nuestro objetivo es maximizar los beneficios totales obtenidos de las reservas de habitaciones al día siguiente de la llegada. Sea 𝑏𝑡 los beneficios obtenidos de las reservas realizadas un número de días t antes del día de llegada. Cuando nos encontramos en el día de llegada (𝑡 = 0), con una ocupación dada 𝑛0, sólo tenemos que maximizar los beneficios esperados el día de llegada 𝑏0. Naturalmente, el beneficio obtenido por las reservas del último día dependerá del precio fijado durante este día. En concreto, queremos elegir el precio 𝑝0 que maximiza el beneficio esperado
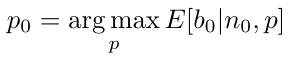
Mientras no se permitan las cancelaciones, el beneficio obtenido en cualquier día 𝑡 es sólo el producto entre el número de habitaciones reservadas la demanda realizada 
, y el precio fijado 𝑝𝑡
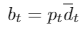
Observa que la demanda realizada es una variable aleatoria, ya que depende de la cantidad demandada, que es a su vez una variable aleatoria cuya distribución viene dada por la ecuación 1. Así, podemos encontrar el valor esperado de la demanda realizada dado un tiempo 𝑡, un precio 𝑝𝑡 y una ocupación actual 𝑛𝑡 sumando todos sus posibles valores ponderados por sus respectivas probabilidades. Entonces, para cada valor posible del precio 𝑝𝑡 fijado en el día 𝑡, podemos calcular el beneficio diario esperado 𝑏𝑡 mediante la sencilla fórmula
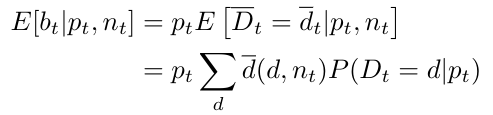
Supongamos que nos encontramos un número de días 𝑡 antes de la llegada, y definamos la función de valor 𝑉𝑡 (𝑛𝑡) como el máximo del beneficio total esperado a partir de ahora, que se consigue fijando un precio óptimo dado que la ocupación actual es 𝑛𝑡. Como argumentamos, si nos encontramos en el día de llegada (𝑡 = 0), la función de valor es simplemente el valor de los beneficios esperados en el día actual, para una elección óptima del precio. Por tanto, utilizando la fórmula anterior podemos escribir
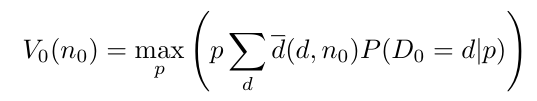
Sin embargo, al fijar los precios con varios días de antelación, nuestro objetivo no es maximizar el beneficio del día actual, sino el beneficio global a largo plazo. Por ejemplo, supongamos que la demanda es baja en este momento, pero tenemos la certeza de que aumentará a medida que se acerque el día de la llegada. En esta situación, si ya tenemos una tasa de ocupación aceptable, podría interesarnos fijar un precio alto y renunciar a algún beneficio en el momento para mantener habitaciones disponibles para las reservas de último momento, que podríamos vender a una tarifa más alta.
El beneficio esperado a partir de ahora dependerá, pues, del beneficio que esperamos en días futuros ( 𝑡’ < 𝑡 ), lo que nos permite definir la función de valor de forma recursiva como
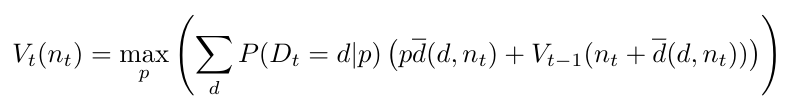
Es decir, el máximo beneficio esperado a largo plazo se alcanzará con el precio que maximiza el valor esperado de la suma entre los beneficios de hoy, expresado por el plazo 
, y los máximos beneficios esperados a partir de mañana. Esto se representa por la función de valor de mañana 
, donde el argumento representa la ocupación de mañana dado que hoy tenemos una demanda 𝑑.
Vemos que para encontrar el valor de 𝑉𝑡 (y por tanto el precio óptimo 𝑝𝑡 que se debe fijar en el día 𝑡 > 0), necesitamos calcular la función de valor para el día siguiente 𝑉𝑡-1, que a su vez requerirá el cálculo de 𝑉𝑡-2 , y así sucesivamente.
En un el post anterior Programación dinámica y la serie de Fibonacci hablamos de cómo la programación dinámica resulta útil en este tipo de problemas recursivos para evitar cálculos repetitivos. En un próximo post mostraremos cómo encontrar el precio óptimo resolviendo la función de valor recursiva con un enfoque de programación dinámica. Mientras tanto, te animamos a visitar la categoría Data Science del blog de Damavis y leer artículos similares a este.
