Programación dinámica
La programación dinámica es un método de programación que consiste en fraccionar un problema complejo en problemas más pequeños, generalmente de forma recursiva. Estos problemas se resuelven de uno en uno, normalmente guardando los resultados ya calculados para evitar cálculos redundantes.
Programación dinámica y la serie de Fibonacci
Un ejemplo paradigmático de un problema que puede resolverse mediante programación dinámica consiste en encontrar el n-ésimo término de la serie de Fibonacci. La serie de Fibonacci se define recursivamente de la siguiente manera:
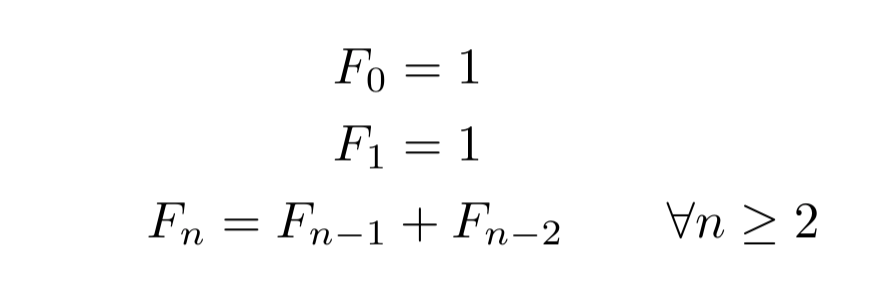
Es decir, para calcular el valor del término n de la serie F𝑛, necesitamos conocer los dos términos anteriores. Por lo tanto, se puede utilizar un enfoque recursivo simple para resolver el problema.
def fibonacci_recursive(n):
if n == 0 or n == 1:
return 1
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)Aun siendo correcta, esta implementación es extremadamente ineficiente. Por ejemplo, si intentamos calcular el cuarto valor de la serie realizando
fibonacci_recursive(4)obtenemos efectivamente el valor correcto F4 = 4. Sin embargo, esta llamada a la función con 𝑛 = 4 desencadenan dos peticiones recursivas a la función con argumentos 𝑛 -1 = 3 y 𝑛 – 2 = 2 . Éstas, a su vez, siguen llamando recursivamente a la función hasta llegar a los casos base F0 y F1.
El siguiente diagrama muestra el flujo seguido para calcular el valor F4 con esta implementación, donde cada casilla representa una petición a la función.
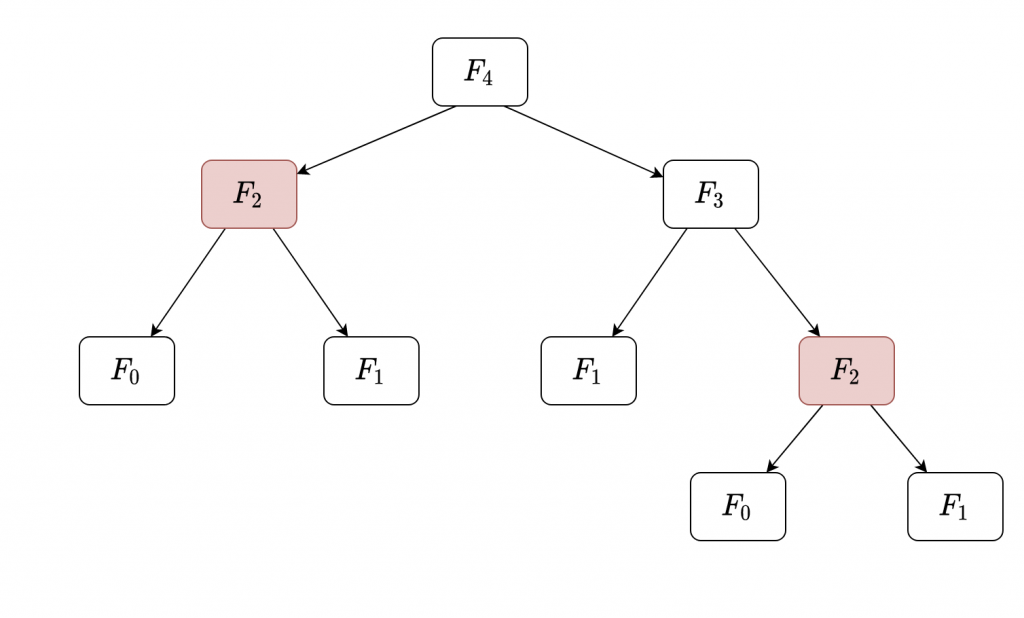
Como podemos observar, la función se ejecuta un total de 9 veces, y hay 4 cálculos de términos no triviales (que no son casos base): uno para F4, otro para F3 y dos para F2. En efecto, los recuadros rojos muestran que el término no trivial F2 se calcula innecesariamente dos veces: una para calcular F4 en la llamada inicial, y otra en el cálculo de F3 .
Dada esta situación, surge la siguiente pregunta: ¿cómo podemos evitar los cálculos repetitivos para calcular el valor de F4? Como habréis imaginado, aquí es donde la programación dinámica entra en acción.
Hemos señalado anteriormente que para calcular el n-ésimo elemento de la serie, tenemos que calcular los dos términos anteriores. Por inducción, se deduce que hay que calcular todos los términos de la sucesión hasta el n-ésimo elemento para encontrar el valor de este.
Dado que necesitamos calcular todos los términos de la secuencia, consideremos el siguiente enfoque: empezaremos estableciendo los casos base triviales, y luego, empezando por el primer término no trivial, calcularemos iterativamente el siguiente elemento utilizando los dos valores anteriores.
El punto clave es que cada vez que calculemos un valor, guardaremos este valor en la memoria de nuestro programa, para poder reutilizarlo siempre que sea necesario en el futuro.
En el ejemplo de la serie Fibonacci, el primer valor no trivial que calcularemos es F2. Observa que, una vez calculado este valor, lo utilizaremos para calcular el siguiente término de la serie, F3 = F1 + F2, y también en el siguiente, F4 = F2 + F3 . De esta manera, aunque se utilizará dos veces, al almacenar su valor conseguimos calcularlo sólo una vez.
Ejemplo de aplicación de un enfoque de programación dinámica
He aquí un ejemplo de la aplicación de un enfoque de programación dinámica para resolver el problema de encontrar el n-ésimo término de la serie de Fibonacci:
import numpy as np
def fibonacci_dp(n):
if n == 0 or n == 1:
return 1
last_value = 1
current_value = 1
for i in range(n-1):
aux_value = current_value
current_value += last_value
last_value = aux_value
return current_valueAunque esta función parece más compleja que la función recursiva definida anteriormente, en realidad es mucho más óptima. En particular, sólo implica n-1 cálculos no triviales que corresponden al cálculo de los términos F2 , F3 , … , F𝑛, una vez cada uno. Esto contrasta con la simple implementación recursiva anterior, que implica un número de cálculos que crece exponencialmente con n.
Por ejemplo, en el caso del cálculo de F5, sólo se necesitan 4 cálculos, mientras que con la función recursiva se necesitarían 7. En el caso de F10, sólo se utilizan 9 cálculos en lugar de 88. Si calculamos F50, utilizando el enfoque de programación dinámica sólo necesitaríamos 49 sumas, mientras que el enfoque recursivo requeriría… ¡20.365.011.073 cálculos!
Conclusión
Este sencillo ejemplo ilustra la importancia de elegir una forma eficiente de abordar un problema, incluso cuando hay diferentes alternativas que dan el mismo resultado; una práctica especialmente importante cuando el problema tiene una naturaleza recursiva que requiere el uso de valores calculados previamente.
En este caso, hemos visto que con sólo almacenar estos valores utilizando un enfoque de programación dinámica, la carga computacional se reduce drásticamente, especialmente a medida que aumenta el número de cálculos anidados.
En futuros posts mostraremos cómo aplicar un modelo de programación dinámica para resolver el problema de la fijación de precios en los hoteles. En particular, lo utilizaremos para calcular el precio óptimo que debe fijarse un número de días antes de la fecha de la estancia, con el fin de maximizar los beneficios a largo plazo.
Mientras tanto, te animamos a visitar la categoría Algoritmos del blog de Damavis para ver más artículos similares a este.
