Introducción
El kernel trick es un método típico en aprendizaje máquina para transformar datos de un espacio original a un espacio de Hilbert arbitrario, normalmente de mayores dimensiones, donde estos son más fácilmente separables (idealmente, linealmente separables). Esta técnica es la base de las Support Vector Machines, ya que éstas, sin kernels, solo pueden separar apropiadamente espacios que sean linealmente separables, pero con el kernel trick pueden operar con virtualmente cualquier espacio, incluso aun si no es euclidiano, como pueden ser moléculas o grafos de amigos de una red social.
En este post queremos no solo enseñar el concepto detrás del kernel trick, sino también poner un ejemplo en un espacio no euclidiano para demostrar visualmente el efecto que tiene kernelizar datos.
Base teórica
Para entender la kernelización primero debemos entender qué es un espacio de Hilbert. Un espacio de Hilbert se define como un espacio de producto interior que es completo con respecto a la norma vectorial definida por el producto interno y, aunque todas las propiedades son importantes, están fuera del alcance de este post, así que nos centraremos en que tiene un producto interno definido. Este espacio es más permisivo que uno Euclidiano y, además, es donde trabajan los datos una vez kernelizados.
Después, necesitamos entender qué es un kernel. Un kernel es una función que recibe dos puntos y retorna un valor, con las propiedades añadidas que la función es simétrica, tal que f(x,v)=f(v,x), y que es una función positiva semidefinida. Si estas propiedades se cumplen, al aplicar la función de kernel, estamos aplicando el equivalente a un producto interno en un espacio de Hilbert arbitrario que corresponde a ese kernel, en muchos casos un espacio desconocido pero que sabemos que existe.
En resumen, cuando aplicamos un kernel sobre los datos, estamos elevándolos a un espacio de Hilbert, en algunos casos, de infinitas dimensiones. Pero solo con esto todavía no tenemos el poder completo de la kernelización: hace falta que el método que estamos aplicando sea también kernelizable y, para eso, simplemente tenemos que tener en cuenta que siempre que se usen puntos, éstos solo se usan para computar productos internos, de tal manera que se pueda reemplazar la función de producto interno por la función de kernel.
Una vez aplicado este cambio, estamos operando en el espacio de Hilbert arbitrario, en vez de el espacio original. Esto es a lo que nos referimos por “kernel trick” y permite elevar los datos a espacios muy interesantes, algunos de ellos teniendo infinitas dimensiones.
Ejemplo práctico
Todo el código para obtener los resultados mostrados en esta sección, e incluso visualizaciones adicionales 3D de los datos, está disponible en el repositorio de Damavis. Las visualizaciones 3D requieren ejecutar el notebook localmente.
Para demostrar la transformación del espacio y la potencia de la kernelizacion, procederemos a clasificar datos moleculares, donde cada punto representa una molécula, y operaremos sobre ellos con SVMs además de visualizarlos con kernel-PCA.
Primero hemos de definir un kernel que pueda operar con grafos,. En nuestro caso, definimos el kernel de Weisfeiler-Lehman, que está basado en un test de isomorfismo en grafos. Una vez definido el kernel, hemos de aplicar el kernel sobre los datos. Para explicar el kernel, usamos pseudo-código, donde G(V,E,l) es un grafo definido por sus nodos (V), sus aristas (E) y las etiquetas de los nodos (l). Una vez los multisets de nodos de cada grafo han sido computados, simplemente obtenemos la intersección de elementos entre los grafos y retornamos el número de elementos en común.
Figura 1: Pseudo-código de kernel de Weisfeiler-Lehman.
Los datos son el dataset MUTAG, formado por 188 grafos, con 17.93 nodos de media por grafo, 2.2 aristas por nodo de media, 125 grafos pertenecientes a la clase 1, y 63 a la clase -1. Un dataset pequeño pero muy conocido para hacer benchmarks de algoritmos sobre grafos moleculares.
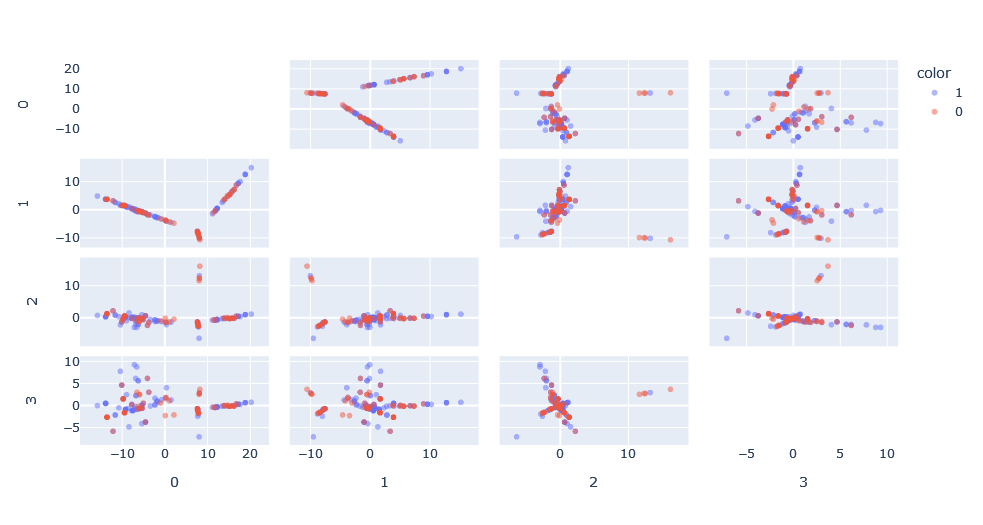
Aplicamos la función de kernel sobre los datos para obtener la matriz de función de kernel y aplicamos kernel-PCA sobre esta matriz para obtener una representación de este espacio. Lo interesante es que podemos ver cómo en las dimensiones principales existen patrones que no habríamos podido ver en su forma de grafo.
Sin embargo, se da el problema de que, comparado con un PCA clásico, no existe el concepto de varianza explicada debido a que el espacio de Hilbert en el cual el PCA está hecho es desconocido. Además, el espacio tiene tantas dimensiones como puntos, por lo que es interesante para visualizar, pero no es muy útil para clasificar.
Otra propiedad interesante de los kernels es que podemos aplicarlos sucesivamente y éstos siguen siendo kernels. Por ejemplo, podemos aplicar el kernel de similaridad del coseno sobre el kernel de Weisfeiler-Lehman, que sería equivalente a la siguiente operación:
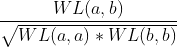
Aplicando esto, podemos ver el nuevo espacio generado. Este espacio, en esencia, ha normalizado los resultados entre 0 y 1 reduciendo así el efecto del tamaño del grafo en el kernel de Weisfeiler-Lehman.
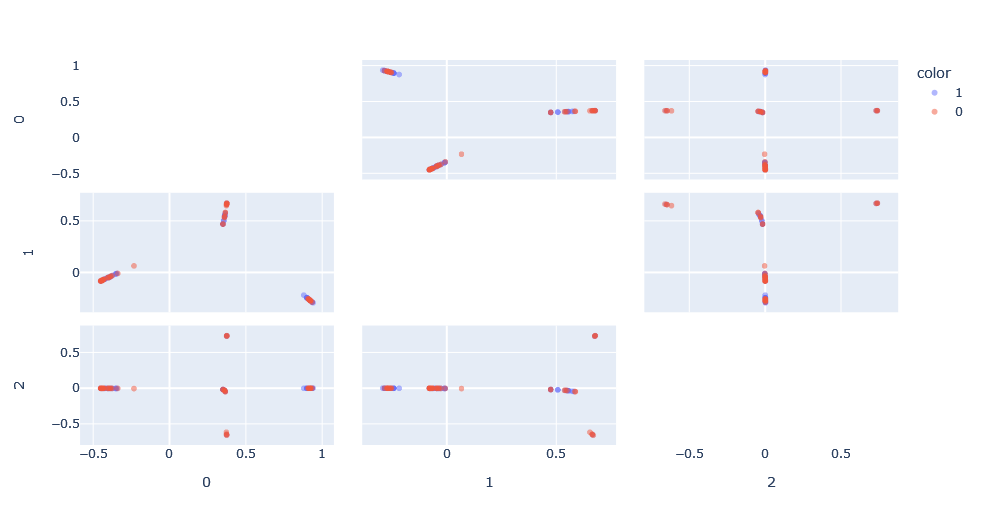
Aplicamos SVM sobre esta composición de kernels, con dos hyper-parámetros a optimizar: h, la profundidad del kernel de Weisfeiler-Lehman y C, la penalización por misclasificación de clase. Haciendo una búsqueda simple, obtenemos la clasificación óptima con C=100 y h=1.
| True 1 | True -1 | |
| Predicted 1 | 9 | 3 |
| Predicted -1 | 1 | 23 |
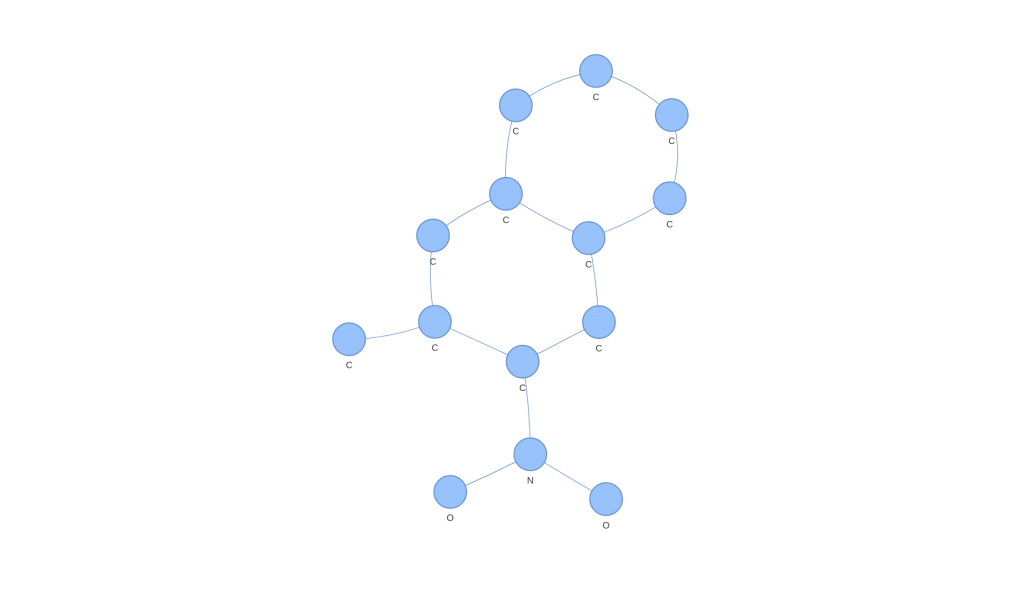
Podemos extraer incluso aquellos grafos moleculares que corresponden a support vectors (aquellos puntos que son usados para obtener el hiperplano que la SVM genera) y observarlos. Por ejemplo, el caso de un support vector de clase 1.
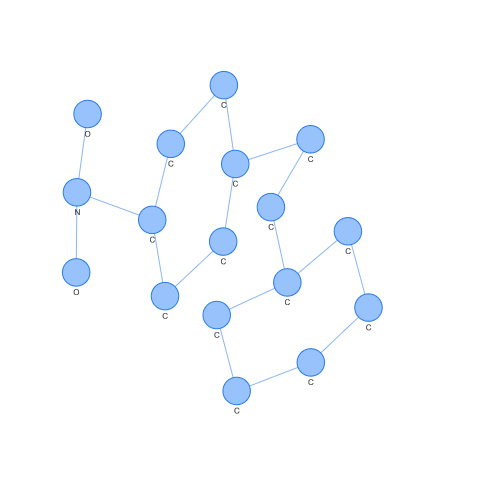
Por el contrario, podemos ver el caso de un support vector de clase -1. Observando ambos, podemos apreciar diferencias a ojo fácilmente, pero lo interesante es cómo estas diferencias han podido ser vistas en un espacio donde SVM o otros algoritmos populares pueden operar.
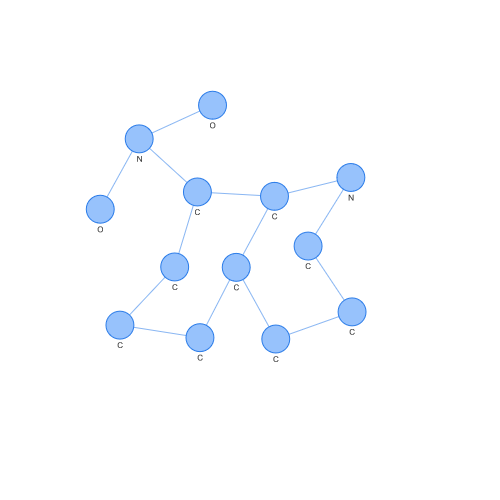
Pero podemos todavía experimentar más con los kernels. Por ejemplo, hay un kernel muy popular que es el kernel RBF (Radial Basis Function), debido a que puede generar un espacio de Hilbert de infinitas dimensiones. Por lo tanto, probemos a modificar nuestro kernel de Weisfeiler-Lehman para trabajar con el kernel RBF.
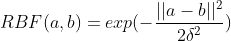
Para poder hacer esto, es necesario pasar de cómo el kernel de Weisfeiler-Lehman calcula las similitudes entre dos grafos a calcular las disimilitudes. En esencia, siendo la distancia euclidiana entre los elementos que pertenecen a grafo A con los elementos que pertenecen a grafo B, usando el nombre de etiquetas de cada sub-árbol como elementos.
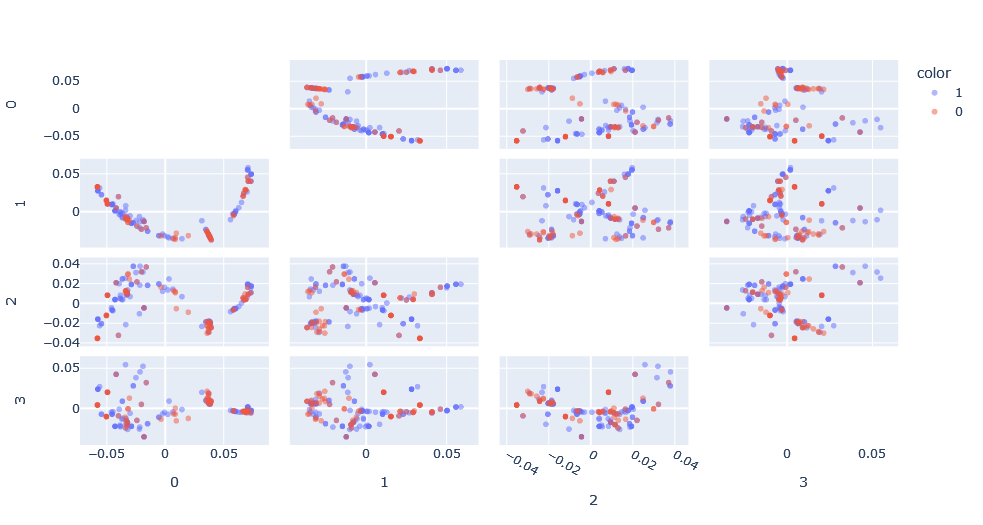
El espacio nuevamente es diferente y los patrones visibles han cambiado, aunque bien podrían ser los mismos patrones vistos anteriormente pero expresados de diferente forma.
Aplicamos SVM de nuevo, con tres hyper-parámetros a optimizar: h, la profundidad del kernel de Weisfeiler-Lehman, C la penalización por misclasificación de clase y δ, el parámetro del kernel RBF. Haciendo una búsqueda simple, obtenemos la clasificación óptima con C=100, h=9 y δ=50.
| True 1 | True -1 | |
| Predicted 1 | 8 | 4 |
| Predicted -1 | 1 | 23 |
El resultado es peor que sin aplicar el kernel Weisfeiler-Lehman con RBF, pero, en entrenamiento, en general daba mejores resultados. Esto es debido a que había más dimensiones en el espacio obtenido haciéndolo más linealmente separable, pero esto también ha llevado a overfitting, que no se producía anteriormente al tratarse de una transformación más simple.
Conclusión
Los kernels pueden transformar nuestros datos de un espacio arbitrario a un espacio de Hilbert arbitrario. Mientras que, normalmente, esto suele ser una transformación de un espacio euclidiano a un espacio de Hilbert, los kernels permiten trabajar con cualquier espacio mientras la función de kernel cumpla con las propiedades esenciales de ser simétrica y positiva semidefinida.
En este post, lo hemos ilustrado usando grafos moleculares como datos que operan en un espacio donde raramente se pensaría que se puede aplicar PCA o SVM, pero que usando el poder de los kernels, es posible.
