Aunque no exista consenso sobre la definición de inteligencia artificial, podemos decir que se trata del conjunto de técnicas por las que un sistema informático puede presentar comportamientos inteligentes.
Existen muchos enfoques, como los sistemas expertos, donde se definen reglas basadas en conocimiento existente sobre una materia y se van disparando según se cumplan unas condiciones. Por otro lado, en la rama del Machine Learning se busca alcanzar dicho comportamiento inteligente a través de un proceso de aprendizaje.
Suele hablarse mucho del aprendizaje supervisado, donde el modelo es alimentado con entradas de datos y sus correspondientes salidas deseadas. Tras un periodo de entrenamiento, el modelo aprende los patrones que relacionan las entradas con las salidas, y es capaz de generalizar funcionando satisfactoriamente con nuevas entradas que no han sido vistas previamente.
Por el contrario, existen modelos donde se aprende sin contar con salidas deseadas, simplemente a partir de los datos en sí mismos. Se trata del aprendizaje no supervisado, donde podemos encontrar las técnicas de Clustering o los modelos generativos.
Sin embargo, existe una tercera variante, el aprendizaje por refuerzo, donde este tiene lugar por medio de la interacción entre un agente y un entorno. En este post estudiaremos Q-learning, una técnica de aprendizaje por refuerzo ideal para introducirse en este campo.
Procesos de decisión de Markov
Como hemos comentado anteriormente, la base de este tipo de técnicas es la interacción del agente con el entorno, que de forma general puede verse como un proceso de decisión de Markov, donde con cada acción que realiza el agente, se actualiza el estado del entorno y se aporta una recompensa, que será un valor numérico que el agente buscará maximizar. A continuación se muestra este flujo tomando como ejemplo el videojuego Ms Pacman:
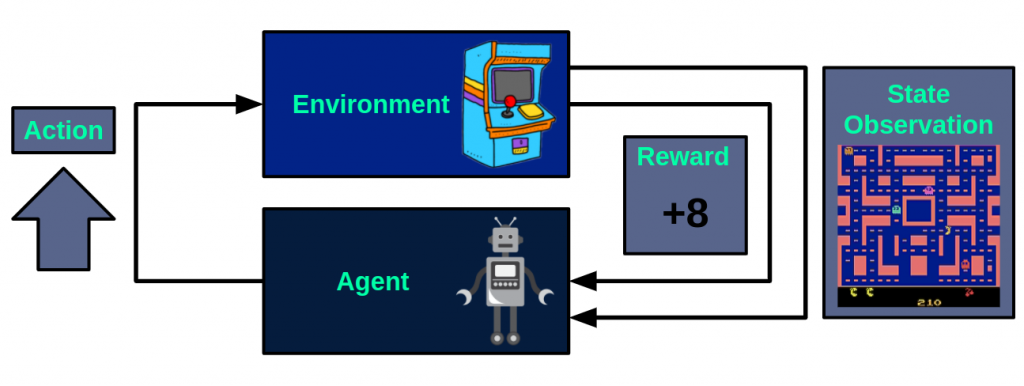
En cada instante, el agente toma una acción de entre las disponibles, en este caso, mover hacia arriba. Tras realizar esta acción, el entorno devolverá la observación del estado resultante, es decir, la imagen siguiente de la pantalla del juego. Además de esto, también se devolverá una recompensa, que será +8.
Partiendo de ese marco, el objetivo del aprendizaje por refuerzo será que el agente aprenda una política que maximice las recompensas obtenidas, considerando la política como la función que para un estado, devuelve la acción a realizar.
La función de valor
Si en cada estado pudiéramos conocer la recompensa acumulada que se puede obtener realizando cada una de las acciones disponibles, está claro que la política que seguiríamos sería la de tomar la acción que nos permita acceder a una mayor recompensa acumulada.
En Q-learning, llamamos Q a la función de valor que nos devuelve la recompensa acumulada esperada de realizar una acción en un estado, sirviendo como medida de la calidad de ese par (estado, acción). Partiendo de esta función, la política a seguir será la de tomar en cada instante la acción con más valor según nuestra función Q.
En su versión tabular, Q será una tabla con tantas filas como estados posibles y tantas columnas como acciones disponibles, donde cada elemento será la aproximación del valor para el par (estado, acción) correspondiente.
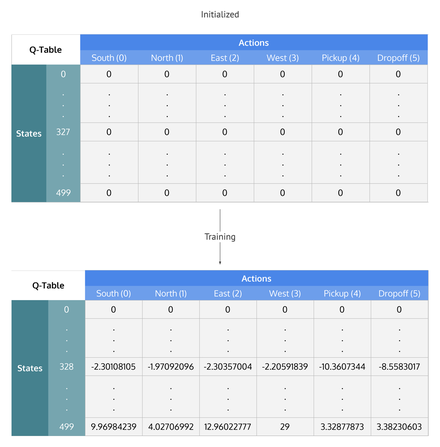
Una vez la tabla es inicializada, iterativamente se irán actualizando los valores de la forma
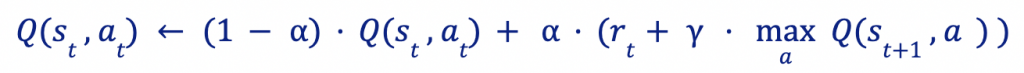
Vemos cómo el nuevo valor conserva parte del original y se actualiza con la nueva información: la recompensa obtenida y el valor del mejor par (estado, acción) para el estado st+1 alcanzado. El parámetro α es un coeficiente de aprendizaje, que determina cuánto se modifica el valor antiguo con la información nueva. Por otro lado, γ es un factor de preferencia temporal que define cuánto se valoran las recompensas futuras frente a las actuales.
El dilema exploración-explotación
Si cuando estamos aprendiendo los valores de la función Q actuamos de forma voraz seleccionando la acción con mejor retorno esperado, es probable que caigamos en un óptimo local, ya que no damos lugar a experimentar con otras variantes que quizá no sean tan buenas a corto plazo pero si sean mejores a largo plazo. Por el contrario, si no vamos poniendo foco en las buenas que vamos encontrando, no iremos acercándonos a mejores soluciones. Por este motivo es importante hacer un buen balance entre explorar nuevos caminos y explotar a partir de los que ya sabemos que son buenos.
Una forma sencilla de obtener este balance es usando Epsilon-Greedy. Para cada instante, con probabilidad ∈ se tomará una acción aleatoria (Exploración) y, en caso contrario, se tomará la acción con mayor retorno esperado (Explotación). Según el valor definido para ∈, se dará más peso a la exploración o a la explotación. Una estrategia inteligente suele ser variar dicho parámetro a lo largo del entrenamiento, de forma que al principio se da más peso a la exploración, y progresivamente se va reduciendo para ir afinando en las mejores soluciones.
Conclusión
La técnica que hemos visto, Q-learning tabular, es muy interesante para introducirse en este campo. Sin embargo, presenta múltiples limitaciones. Por un lado, si el entorno es relativamente complejo, tener una tabla con todas las combinaciones de estados y acciones resulta inabordable. Además, este enfoque no es capaz de trabajar de forma directa con espacios de estados y acciones continuos.
En futuras entradas veremos Deep Q-Network, una variante de Q-learning donde se reemplaza la tabla por una red neuronal, mitigando así las limitaciones de la versión tabular.
