Introducción a la Regresión Logística

La regresión logística es una metodología estadística que permite modelar las relaciones entre una variable categórica binaria y un conjunto de variables explicativas. Específicamente, se modela la probabilidad de que una observación pertenezca a una de las categorías de dicha variable binaria. En este post veremos las características básicas del modelo así como su implementación en Python.

Variables categóricas

Una variable categórica o cualitativa es una variable que nos indica la pertenencia de la observación a un grupo y por lo tanto no toma valores numéricos. Ejemplos de estas son el sexo de una persona, la nacionalidad o si una persona es fumadora o no. En el caso de que solo existan dos grupos, la variable se denomina dicotómica o binaria, mientras que si existe más de una categoría, se denomina politómica.

Debido a que los valores de una variable cualitativa son categorías el problema de predecir el valor de una variable categórica se suele denominar clasificación, sobre todo en el ámbito del aprendizaje automático.   

En algunas ocasiones se suele asignar números a cada una de las categorías de una variable categórica. Por ejemplo, una práctica habitual es codificar las variables dicotómicas asignando a una de las categorías el número 1 y a la otra el 0. Esta codificación 0-1 permite además una interpretación en términos de probabilidad ya que podemos identificar el número asignado como la probabilidad de que la observación pertenezca a una categoría.   

La sustitución de categorías por números nos permite aplicar la regresión lineal para modelar la probabilidad de pertenencia a una categoría pero esto tiene diversos inconvenientes:

• Se violan diversos supuestos de la regresión lineal, lo que imposibilita la correcta inferencia estadística.
• Los valores predichos pueden caer fuera del rango de la variable. Por ejemplo, valores mayores que 1 en una variable dicotómica codificada con 0 y 1.

Regresión Logística

La regresión logística nos permite sortear los problemas de la regresión lineal. Para verlo pensemos en el siguiente problema. Supongamos que tenemos datos acerca de los pasajeros del Titanic y que queremos ver cuáles de sus características están relacionadas con la probabilidad de supervivencia. Si definimos como una variable que toma el valor 1 si la persona sobrevivió y 0 en caso contrario, estamos interesados en encontrar una función tal que:

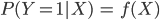
Donde es un vector de características del pasajero.

La regresión lineal definiría

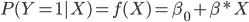
Donde es un vector de parámetros que habría que estimar junto con el parámetro . Se observa que para valores extremos de se podrían obtener valores por encima de 1 o por debajo de 0.

Por su lado, la regresión logística define como la función logística:

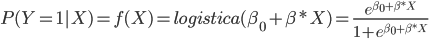
Esta función usada en la regresión logística tiene 2 propiedades interesantes. La primera es que su forma resuelve el problema de que las predicciones puedan estar fuera del intervalo (0,1):

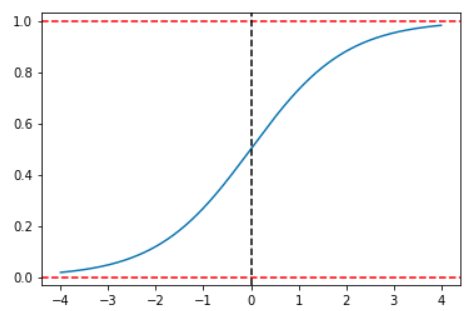
Como se puede observar en esta gráfica, un cambio de depende no solo del cambio en la variable independiente sino que también depende del nivel de la variable dependiente desde el que se produce el cambio. Esto hace que una interpretación de los coeficientes no sea posible más allá del signo de los mismos. Sin embargo, un poco de manipulación algebraica nos permitirá establecer una interpretación. Recordemos que en el caso de una variable dicotómica solo existen dos posibilidades por lo que

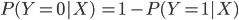
Si calculamos el ratio de las probabilidades de las dos categorías obtenemos:

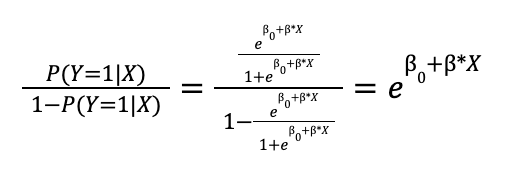
La fracción se denomina odds o cuota, un concepto extraído del mundo de las apuestas e indica cuantas veces más probable es obtener una observación de la categoría 1 respecto a la categoría 0. Aplicando logaritmo a ambos lados de esta fracción nos quedaría:

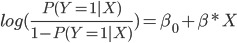
Por lo que, al usar una función logística, establecemos una relación lineal con el logaritmo de los odds y podemos interpretar los coeficientes de la siguiente manera: por cada incremento de una unidad en el logaritmo de los odds varía en promedio unidades, o lo que es lo mismo, por cada incremento de una unidad en los odds se ven multiplicados en promedio por .

Para la estimación de los parámetros se suele usar una metodología llamada estimación por máxima verosimilitud que trata de hallar los valores de los parámetros que maximizan la función de verosimilitud para la muestra de n observaciones:

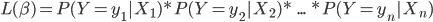
Ejemplo de Regresión Lineal en Python

Datos

Para ejemplificar el uso de la regresión logística usaremos uno de los conjuntos de datos de Kaggle. Para descargarlos podemos ir aquí. En este dataset, cada fila representa una persona que estuvo a bordo del Titanic y cada columna es una característica del pasajero, incluyendo si sobrevivió al choque del barco que será la variable que intentaremos predecir.

Podemos descargar dos conjuntos de datos, train.csv lo usaremos para calcular nuestro modelo mientras que test.csv lo usaremos para evaluar el desempeño del mismo con datos desconocidos para el modelo.

Para entrenar el modelo nos quedamos solo con las variables ‘Survived’, ‘Sex’, ‘Age’, ‘SibSp’, ‘Parch’,  ‘Fare’ y ‘Embarked’:

columns_to_use = [i for i in train.columns if i not in
                  ["PassengerId", "Name", "Cabin", "Ticket", "Pclass"]]

La variable ‘Sex’ tiene algunos valores faltantes por lo que haremos una simple imputación usando la media del conjunto para poder utilizar todos los datos. Para facilitar esta imputación podemos usar la clase SimpleImputer de Scikit-learn:

#Imputación de valores perdidos en la edad

imp = SimpleImputer()
imp.fit(train[["Age"]])
train.loc[:, "Age"] = imp.transform(train[["Age"]]).reshape((1,-1))[0]

La variable a predecir ‘Survived’ está ya codificada con 0 asignado a los que no sobrevivieron y 1 a los que sí. Sin embargo, algunas  de las variables son categóricas y tienen aún las etiquetas, por lo que hay que modificarlas para que podamos usarlas en la regresión. Para ello, haremos un proceso llamado one hot encoding en el que generamos tantas variables como categorías tiene la variable colocando 0 si la observación pertenece a la categoría denotada en la nueva variable y 0 en otro caso. Pandas nos permite hacer esto de una manera sencilla con la función get_dummies:

#Creación de dummies

train_dummies = pd.get_dummies(train[columns_to_use], drop_first=True)

#Añadir una constante a los datos 

train_dummies.loc[:, 'const'] = 1

El parámetro drop_first=True nos permite eliminar la primera categoría de cada variable ya que no es necesaria en la regresión al poderse representar como la categoría base, es decir, la que se obtiene por defecto cuando todas las otras categorías tienen asignado un 0. 

Paquetes de Python para Regresión Logística

Existen diversos paquetes o librerías que implementan la regresión logística en Python. Dos muy conocidos son Statsmodels y Scikit-learn. En este post usaremos Statsmodels por tener una forma sencilla de obtener tests de significancia para los coeficientes de la regresión.  

Para entrenar un modelo de regresión logística con Statsmodels y obtener un resumen de los resultados usamos el siguiente código:

model = sm.Logit(train.Survived, 
                 train_dummies.loc[:, [i for i in train_dummies.columns 
                                       if i not in ["Survived"]]])

result = model.fit()
result.summary()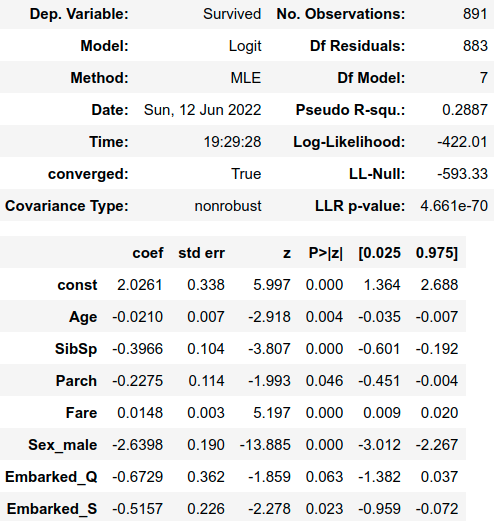

Evaluación de los resultados

En la columna “P>|z|” del resumen nos encontramos con p-valores para la hipótesis que los coeficientes son estadísticamente diferentes de cero. Observando esta columna y usando un umbral del 10% podemos destacar varios detalles interesantes. 

El primero es que solo la variable “Fare” tiene una influencia positiva y significativa sobre la probabilidad de supervivencia. Específicamente, al dejar todas las otras variables constantes, un dólar adicional que se haya gastado el pasajero en su billete, provoca que los odds de sobrevivir a no sobrevivir se vean multiplicados por , o lo que es lo mismo aumenta en promedio los odds de supervivencia en un 1.5%.

Los más jóvenes parecen haber tenido más suerte ya que el coeficiente de “Age” tiene un coeficiente negativo y significativo que nos indica que la probabilidad de supervivencia se ve disminuida al aumentar la edad.

El número de familiares parece tener una influencia negativa en la probabilidad de supervivencia, como indican los coeficientes negativos de SibSp y Parch.

La variable “Sex_male” tiene un coeficiente negativo y diferente de cero, por lo que pertenecer al grupo de hombres Sex_male=1 está relacionado con una probabilidad de supervivencia más baja que la del grupo de mujeres Sex_female=0.

En último lugar, los pasajeros que embarcaron en Queenstown y Southampton en promedio parecen tener menos probabilidades de supervivencia al compararlos con los que embarcaron en Cherbourg como lo indican los coeficientes negativos y significativos de Embarked_Q y Embarked_S.

Hasta ahora, la regresión nos ha mostrado la relación que existe entre algunas variables y la probabilidad de supervivencia, pero si queremos clasificar nuevas observaciones necesitamos transformar las probabilidades en una categoría. Lo que suele hacerse con las predicciones es utilizar un umbral, típicamente 0.5, y etiquetar como de la clase 1 las observaciones con probabilidades mayores a este.

Para hacer predicciones con Statsmodels podemos usar la propiedad predict() de un modelo entrenado para obtener las probabilidades de supervivencia y aplicar un umbral para obtener las categorías. Usando sklearn podemos entender que tan buenas son nuestras predicciones con los datos de entrenamiento:

confusion_matrix(train_dummies.Survived, result.predict()>0.5)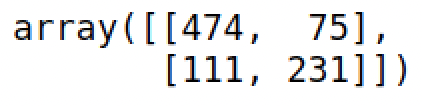

accuracy = accuracy_score(train_dummies.Survived, 
                          result.predict() > 0.5)
accuracy = round(100*accuracy, 2)
print(f'Accuracy: {accuracy}%')

Por lo que nuestro modelo logra clasificar correctamente el 79.12% de las observaciones. Para comparar podemos estimar un modelo de regresión lineal:

model_lin = sm.OLS(train.Survived, 
                   train_dummies.loc[:, [i for i in
                                         train_dummies.columns 
                                         if i not in ["Survived"]]])
result_lin = model_lin.fit()
accuracy = accuracy_score(train_dummies.Survived, 
                          result_lin.predict() > 0.5)
accuracy = round(100*accuracy, 2)
print(f'Accuracy: {accuracy}%')

Obtenemos porcentajes parecidos con ambos modelos, pero como muestra el siguiente gráfico donde cada punto es un pasajero, en ocasiones tendemos a predecir probabilidades fuera del (0,1):

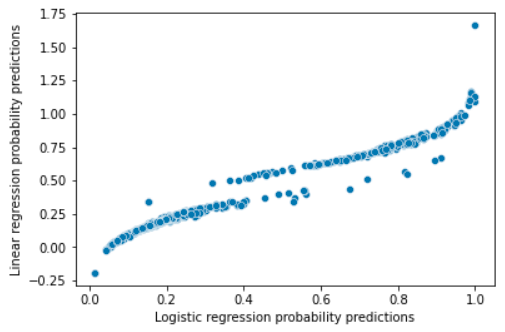
Además, debido a que se violan algunos supuestos de la regresión lineal como la normalidad de los errores o la homocedasticidad, no es correcto utilizar los intervalos de confianza o los p-valores para determinar si las relaciones entre las variables son significativas.

Conclusión

En este post hemos introducido algunos conceptos básicos de la regresión logística y la interpretación de sus parámetros. Por otro lado, hemos implementado este modelo en Python usando Statsmodels y un conjunto de datos de ejemplo, comparando su desempeño con el de la regresión lineal.

¡Esto es todo! Si este post te ha parecido interesante, te animamos a visitar la categoría Data Science para ver todos los posts relacionados y a compartirlo en redes. ¡Hasta pronto!