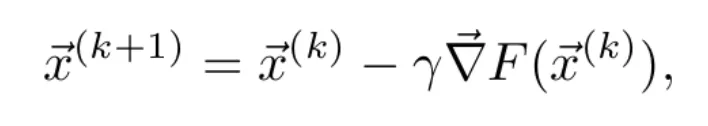Uno de los problemas más comunes en ciencia de datos es el de la predicción del valor de ciertas variables a partir de otras. Por ejemplo, debemos saber si es conveniente conceder un préstamo a un cliente dependiendo de factores como su edad, sus ingresos mensuales, etc. Para ello, simplemente debemos clasificar cada caso en dos categorías, si concedemos el préstamo o no. Por lo tanto, estamos ante un problema de clasificación.
Otro ejemplo sería estimar el precio de una vivienda a partir de sus características (antigüedad, superficie, número de habitaciones, ubicación…). En este caso, queremos predecir una cantidad (el precio de la casa). Esto se considera un problema de regresión.
Los problemas de clasificación y regresión constituyen las dos clases principales de lo que se llama aprendizaje automático supervisado. En este paradigma, un modelo matemático es entrenado para aprender a predecir una o más variables (variables dependientes u objetivo) a partir de otras (variables independientes).
Predicciones y relaciones entre variables
Para entender cómo están relacionadas entre sí las distintas variables y poder emitir una predicción, necesitamos partir de un conjunto de observaciones. En el ejemplo de estimación de precios de una casa, deberíamos tener muchos ejemplos de viviendas de las que conozcamos tanto las variables independientes (antigüedad, superficie y las demás características) como la dependiente (su precio). En el proceso de entrenamiento, el modelo debe entender cómo afectan las distintas características de la casa a su precio. Así, posteriormente, será capaz de predecir el precio de una casa conociendo solamente las demás variables.
Existen modelos de aprendizaje supervisado muy diversos que sirven para abordar problemas tanto de clasificación como de regresión. Entre los algoritmos más populares está el de K-Nearest Neighbors (usado, sobre todo, para clasificación), la regresión logística (para clasificación y regresión) o la regresión lineal (para regresión).
Sin embargo, la mayoría de estos algoritmos tienen limitaciones para resolver problemas donde la estructura de los datos es relativamente compleja. Así, por ejemplo, la regresión logística falla para problemas de clasificación en los que los datos no son linealmente separables.
Para resolver problemas complejos, en las últimas décadas se han desarrollado y popularizado un conjunto de modelos con una estructura común. Las conocidas como redes neuronales artificiales.
Las redes neuronales artificiales
Empecemos por lo básico: ¿qué son las neuronas? Son las células encargadas de la propagación del impulso nervioso a través del sistema nervioso de los animales.
Estas células constan de dos partes principales. Por un lado, el cuerpo celular o soma, del que sobresalen unas prolongaciones cortas llamadas dendritas. Y, por otro, una prolongación larga, llamada axón, conectado con otras neuronas. Las dendritas son las encargadas de transmitir los impulsos que reciben de otras células hacia el soma. Desde aquí, se propaga a través del axón. Finalmente, se transmite a otra neurona mediante la sinapsis neuronal (o bien, a una célula motora).
Así pues, las redes neuronales están formadas por billones de neuronas conectadas entre ellas. Es esta arquitectura la que permite el aprendizaje de los animales.
Las redes neuronales artificiales pretenden imitar el funcionamiento de las redes neuronales biológicas. De la misma manera que éstas se componen de neuronas, la principal unidad constituyente de las redes neuronales artificiales es el perceptrón simple. El perceptrón no es más que la representación matemática de una neurona. De hecho, imita su estructura y las funciones de cada una de sus partes. No en vano, se le suele llamar también una neurona artificial. Veámoslo.
El perceptrón simple
Un perceptrón se puede definir como una función matemática f que permite relacionar un vector de variables independientes x⃗ = (x1,… ,xN), con una variable dependiente y, de manera que se estima la variable independiente como ŷ = f(x⃗) . Esta función está parametrizada por un vector de pesos, ω? =(ω1,…,ωN)T , que ponderan la influencia de cada una de las variables independientes en el valor de la variable dependiente; y por una función φ, (función de activación), de manera que
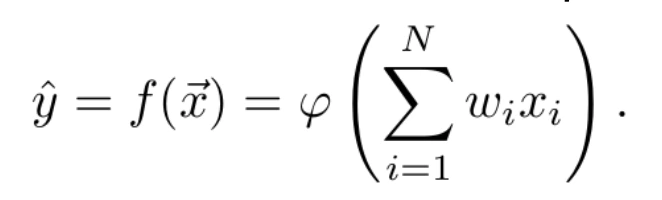
De hecho, la combinación lineal se puede expresar como un producto escalar entre el vector de variables independientes y el de pesos. De esta manera, la ecuación anterior puede expresarse como:
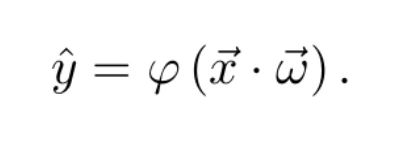
Neurona biológica y neurona artificial
Hasta aquí, tal vez no se vea el parecido del perceptrón con una neurona. Pero ¿qué tal si lo pintamos así?
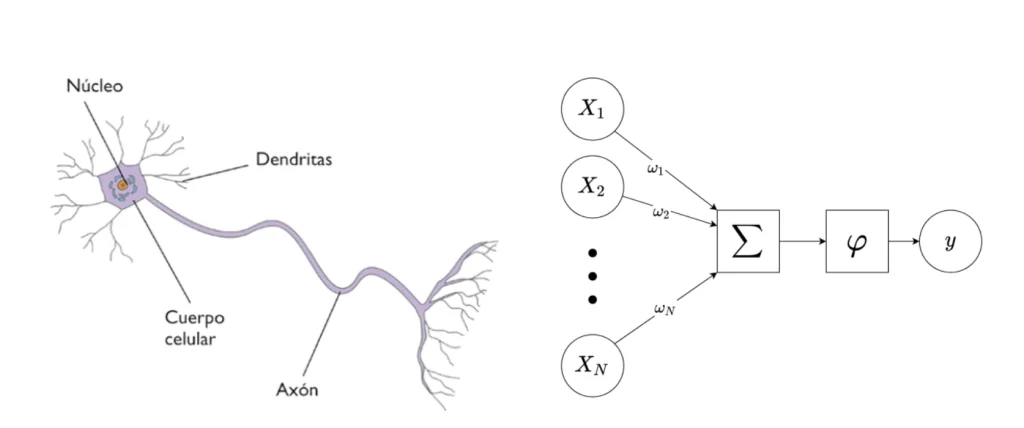
Estudiemos a partir de la Figura 1 la analogía entre una neurona biológica y una neurona artificial. Cada una de las variables de entrada (aquí los x1,… ,xN) representa la señal recibida por la neurona a través de la sinapsis con una neurona vecina. Todos estos inputs se combinan entre ellos a través de una sencilla operación. Cada valor xi de entrada se multiplica por un peso ωi. Este peso pondera la contribución de dicha variable en el cálculo de la variable dependiente. A continuación, se suman todas estas contribuciones.
Esta operación simula la transmisión y la combinación de todas las señales de entrada a través de las dendritas hacia el centro de la neurona. Finalmente, el efecto de la función de activación φ sobre la suma ponderada representa cómo se propaga la información a través del axón.
Función de activación y función escalón
La función de activación transforma el resultado de la combinación lineal entre las variables independientes y sus pesos asociados. Tal y como su nombre indica, su objetivo es determinar el nivel de activación de la neurona. La más sencilla función de activación es la llamada función escalón, definida como
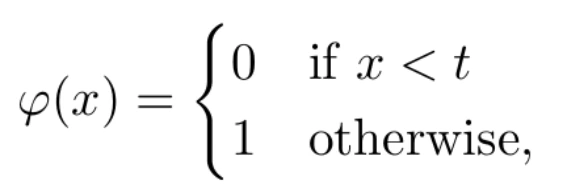
donde t es un parámetro del modelo. Con este ejemplo, el resultado de la neurona será 1 (decimos que la neurona se activará, o que su información se propagará a través del axón) sólo si la combinación lineal supera el valor umbral t. En caso contrario, su resultado será 0. Esta función, si bien es muy intuitiva, tiene el inconveniente de no ser derivable. En el proceso de aprendizaje, necesitaremos que la funciones involucradas sean derivables. Por eso, se opta por otras funciones de activación. Una de las más usadas es la función logística, definida por la fórmula
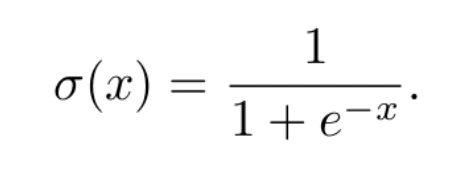
Esta función sí es derivable, y de hecho su derivada cumple la sencilla ecuación
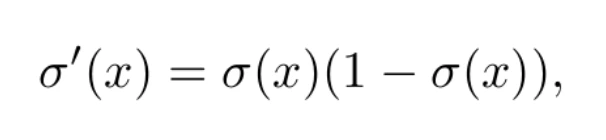
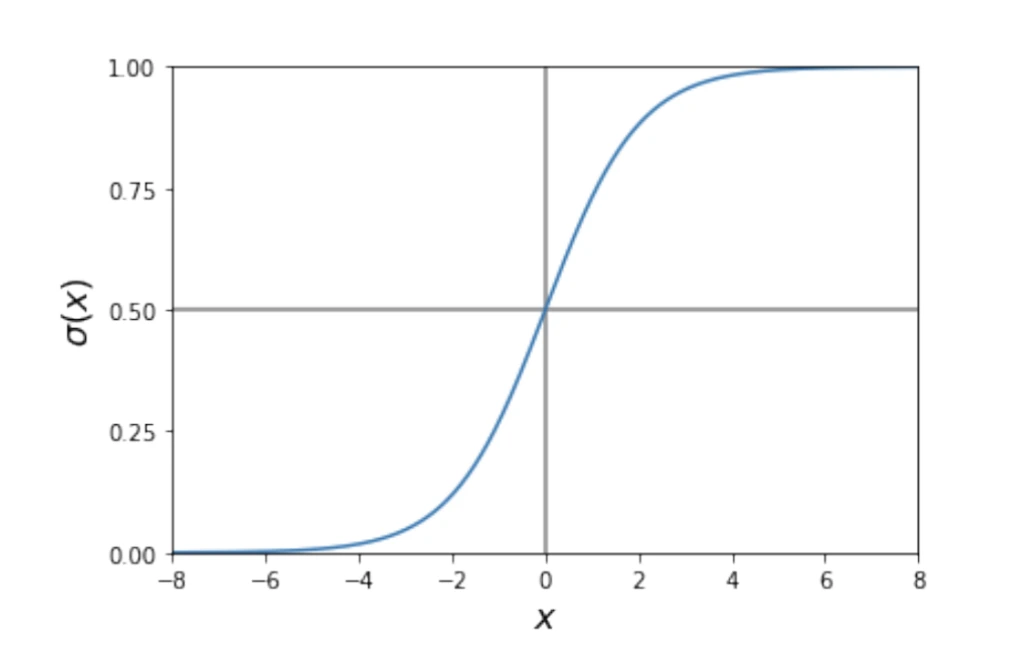
lo que facilita mucho el proceso de aprendizaje. La forma de la función logística puede verse en la Figura 2. Para valores arbitrariamente positivos de x, tiende a uno. En el caso de valores arbitrariamente negativos, tiende a 0, cumpliéndose que σ(0) = 0.5 . Así, la neurona se activará (ŷ = 1) si la combinación lineal es muy positiva. En cambio se apagará (ŷ = 0) si es muy negativa.
Aprendizaje del perceptrón
Ahora bien, ¿en qué consiste el proceso de aprendizaje del perceptrón? Se trata de encontrar los pesos ωi que mejor se ajustan a los datos de los que disponemos.
Estos datos consisten en un conjunto (preferiblemente grande) de observaciones en las que conocemos tanto las variables independientes como la que se quiere predecir. La idea es que, para cada ejemplo de entrada, el modelo trate de predecir la variable objetivo a partir de las variables independientes. Al principio se equivocará mucho. Sin embargo, como conocemos el valor real de la variable a predecir, irá corrigiéndose tras cada predicción para que cada vez dé mejores resultados.
El primer paso en cualquier algoritmo de aprendizaje supervisado es dividir el dataset en dos conjuntos. Por un lado, el conjunto de entrenamiento y, por otro, el conjunto de test. El primer conjunto, como su nombre indica, es el que usaremos para entrenar el modelo. El segundo, se usará para validar el modelo una vez terminado el proceso de entrenamiento.
La función de pérdidas
Para evaluar lo buena que es una predicción y dar feedback al modelo durante el entrenamiento, debemos definir una función de pérdidas. Esta función J(ŷ, y) debe cuantificar el error cometido en la estimación del valor de y en cada predicción ŷ.
En los problemas de regresión, donde la variable dependiente es continua, la elección más simple sería tomar el valor absoluto de la diferencia entre el valor real y el predicho. Esto es, J(ŷ, y) = |ŷ − y|. Sin embargo, de nuevo, nos encontramos con que esta función no cumple con la deseada propiedad de la derivabilidad. Por tanto, se prefieren usar otras funciones de pérdidas.
Una de las más simples (y también de las más usadas) es la diferencia cuadrática, definida por la ecuación
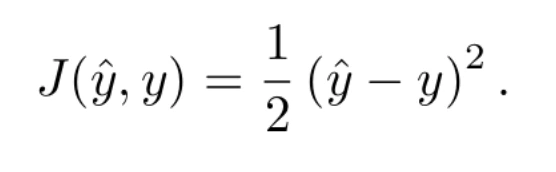
Esta ecuación tiene la ventaja de que sí es derivable. De hecho, su derivada puede expresarse como
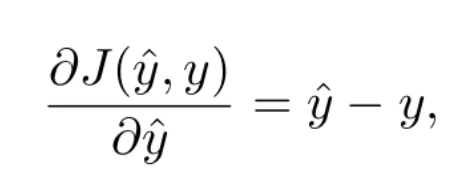
que no es más que el error (con signo) cometido en la predicción.
El descenso del gradiente
¿Por qué tanto énfasis en que las funciones sean derivables? La razón es que para encontrar el valor de los pesos que resuelven el problema, la red neuronal se basa en un método iterativo, el descenso del gradiente.
Cómo funciona
Dicho método tiene como objetivo encontrar el mínimo de cierta función F a partir del cálculo de su gradiente. Es decir, de la derivada respecto a sus parámetros de entrada x⃗. El método funciona de la siguiente manera:
- Se realiza una primera estimación de los parámetros de entrada, x⃗(1), o bien se inicializan aleatoriamente.
- Para cada iteración k =1, 2, …
- Se calcula el gradiente de la función respecto de los parámetros actuales

- Puesto que el gradiente apunta en la dirección de máximo crecimiento de la función y el objetivo es minimizar dicha función, se actualizan los parámetros introduciendo una pequeña variación en el sentido opuesto al del gradiente. Se aplica la regla

donde 𝛄 es un número real que determina cuánto se modifican los parámetros en cada iteración. Para 𝛄 suficientemente pequeño, se cumple que . Es decir, para cada iteración se irá reduciendo el valor de la función.
. Es decir, para cada iteración se irá reduciendo el valor de la función.
- Se calcula el gradiente de la función respecto de los parámetros actuales
- Criterio de parada. Podemos fijar un número máximo de iteraciones, o bien un umbral mínimo en la variación de los parámetros. La idea detrás del segundo método es parar cuando se obtienen gradientes cercanos a cero. En el caso en que F sea una función convexa, esto nos indica que estamos cerca del mínimo absoluto.
Descenso del gradiente y perceptrón
En el caso del perceptrón, nuestro objetivo es encontrar el vector de pesos ω⃗ que minimiza la función de pérdidas. Para ello, necesitamos ser capaces de calcular el gradiente de la función de pérdidas respecto de los pesos a partir del resultado del entrenamiento. Por eso, necesitamos que todas las funciones involucradas en el proceso sean derivables. Así, sea ![]() el vector de pesos en la iteración k, la regla de actualización (Ecuación 8) es
el vector de pesos en la iteración k, la regla de actualización (Ecuación 8) es
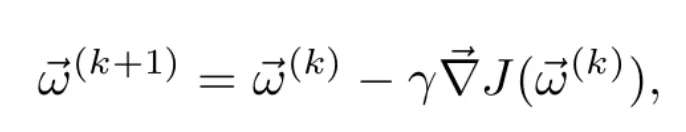
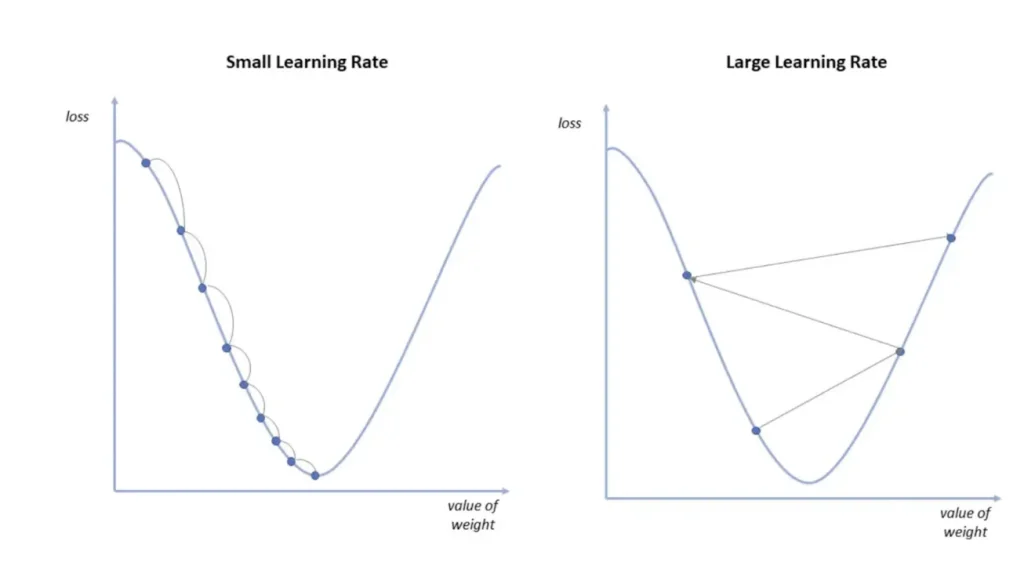
donde el learning rate (ratio de aprendizaje) 𝛄 puede fijarse como hiperparámetro del modelo o ajustarse según avanza el entrenamiento. Una técnica habitual, sobre todo en caso de funciones de pérdidas convexas respecto a los pesos, es usar un ratio de aprendizaje decreciente a lo largo del entrenamiento. De esta manera, a medida que nos acercamos al mínimo, las variaciones en los pesos son más pequeñas. Así, se evita salir de la cuenca de atracción del mínimo u oscilar indefinidamente alrededor de él (ver Figura 3).
Variaciones del descenso del gradiente
En general, el método del descenso del gradiente en las redes neuronales consiste en recorrer todo el conjunto de entrenamiento (normalmente varias veces), donde a cada bucle sobre todos los ejemplos se le llama un epoch. Los pesos se van actualizando a lo largo del entrenamiento. Dependiendo de cuándo y cómo se aplica esta actualización, tenemos distintas variantes del descenso del gradiente. Las resumimos a continuación.
Descenso del gradiente en batch
En esta modalidad del descenso del gradiente, se actualizan los pesos tras completar cada epoch. Es decir, cada vez que se ha recorrido todo el conjunto de entrenamiento. De esta manera, se toma la contribución de todos los ejemplos de entrenamiento sobre el gradiente de la función de pérdidas. Además, se actualizan los pesos de manera que se minimice el error sobre todo el dataset.
Esta técnica da resultados muy buenos cuando las funciones de pérdidas son convexas o relativamente suaves. Esto se debe a que converge directamente hacia el mínimo (local o absoluto). Sin embargo, tiene una gran desventaja. Para conjuntos de datos relativamente grandes (como suele ser el caso), es computacionalmente muy costoso.
Descenso del gradiente estocástico
En esta variante, se van actualizando los pesos con cada ejemplo de entrenamiento. Una vez que se ha completado una epoch, es habitual reordenar aleatoriamente el conjunto de entrenamiento antes de volver a empezar el bucle. Así, se evita que un orden fijado pueda afectar al resultado.
Esta técnica tiene la ventaja de que es computacionalmente muchísimo más ágil que la anterior. Sin embargo, como su nombre indica, la evolución de la función de costes se vuelve estocástica. En cada iteración, se reduce el valor de la función de costes sobre el ejemplo en cuestión.
No obstante, es posible que la función de costes global empeore. Esta propiedad puede ser deseable cuando la función de pérdidas no es convexa, ya que nos permite salir de la cuenca de atracción de un mínimo local hacia otro mínimo local mejor. Sin embargo, no asegura la convergencia hacia el mínimo, ya que, debido a su naturaleza estocástica, tiende a oscilar.
Descenso del gradiente en minibatch
Esta variante combina lo mejor de las dos anteriores. En lugar de usar un solo ejemplo de entrenamiento o todos ellos, se usa un subconjunto de ejemplos de entrenamiento. Este subconjunto, conocido como minibatch, se usa para actualizar los pesos en cada iteración hasta haber recorrido todo el dataset tras n=M/k iteraciones. (Donde M es el número de ejemplos de entrenamiento y k es el tamaño del minibatch).
Al igual que en el ejemplo anterior, una vez que se han recorrido todos los ejemplos, se suelen reordenar para asegurar la aleatoriedad. De esta manera, al tener una muestra más representativa del total que un solo ejemplo, la contribución promedio del minibatch suele hacer que la función de costes total tienda a reducirse en cada iteración.
No obstante, la aleatoriedad deja hueco para una posible salida de un mínimo local sub-óptimo hacia un mínimo mejor. El tamaño del minibatch k es un hiperparámetro del modelo. El balance ideal es que sea suficientemente pequeño para escapar de los mínimos sub-óptimos, pero suficientemente grande para converger en caso de encontrarse cerca del mínimo global, los cuales suelen tener cuencas de atracción más amplias y profundas.
Ya hemos podido elegir la modalidad del descenso del gradiente según las características de nuestro problema. Solamente nos faltaría calcular el gradiente de la función de pérdidas respecto los pesos que aparecen en la Ecuación 9.
Cálculo del gradiente de la función de pérdidas
Supongamos, de momento, que usamos el descenso del gradiente estocástico. Más adelante, veremos cómo se generaliza a las demás variantes. Sea (x⃗, y) el ejemplo de entrenamiento en cuestión e ŷ la predicción obtenida usando el vector de pesos actual ω⃗. Sabemos que la función de costes J(ŷ, y) depende del valor predicho ŷ, que a su vez depende de ω⃗. Por ello, para calcular su gradiente respecto de los pesos usamos la regla de la cadena:
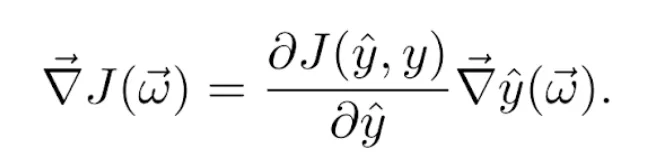
El gradiente del valor predicho respecto de los pesos, lo encontramos usando la regla de la cadena sobre la Ecuación 2. De manera, que
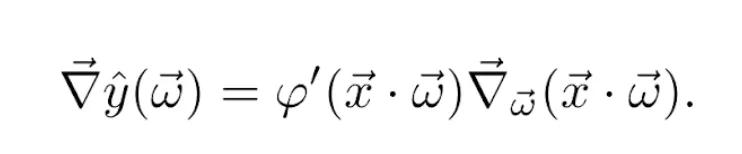
El gradiente del producto escalar respecto del vector de pesos es x⃗. Por tanto, juntando las Ecuaciones 9, 10 y 11, la actualización de los pesos se convierte finalmente en la regla
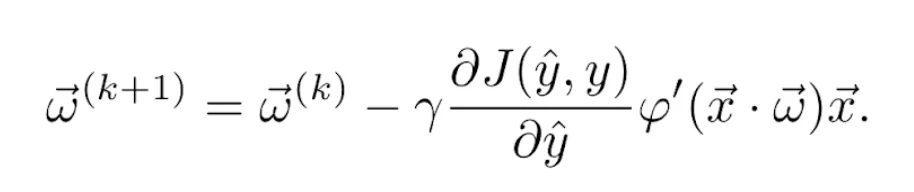
Por ejemplo, si se usa la función de activación logística definida en la Ecuación 4 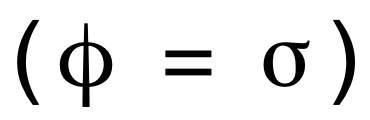 y la función de pérdidas cuadrática definida en la Ecuación 6, sus derivadas vienen dadas, respectivamente, por las Ecuaciones 5 y 7. Por tanto, la regla de actualización se convierte en
y la función de pérdidas cuadrática definida en la Ecuación 6, sus derivadas vienen dadas, respectivamente, por las Ecuaciones 5 y 7. Por tanto, la regla de actualización se convierte en
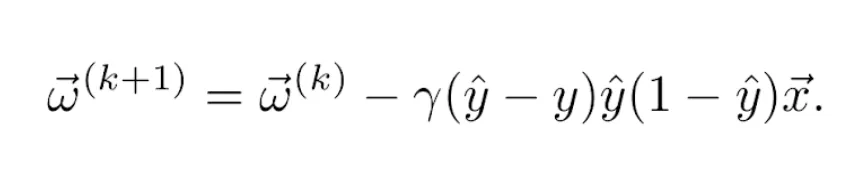
En el caso del descenso del gradiente en batch o minibatch, suele considerarse la función de pérdidas como la suma de los errores cometidos en las predicciones 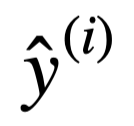 de todos los ejemplos de entrenamiento
de todos los ejemplos de entrenamiento 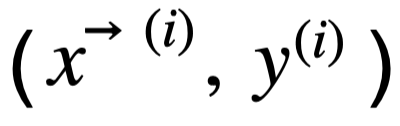 considerados en cada iteración. (En el caso del descenso del gradiente en batch, el número total de ejemplos es M. En el caso del gradiente en minibatch, el tamaño del minibatch es k):
considerados en cada iteración. (En el caso del descenso del gradiente en batch, el número total de ejemplos es M. En el caso del gradiente en minibatch, el tamaño del minibatch es k):
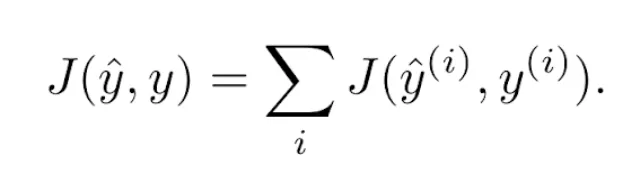
La derivada del sumatorio es igual al sumatorio de las derivadas. Por tanto, la regla de actualización de los pesos se convierte en
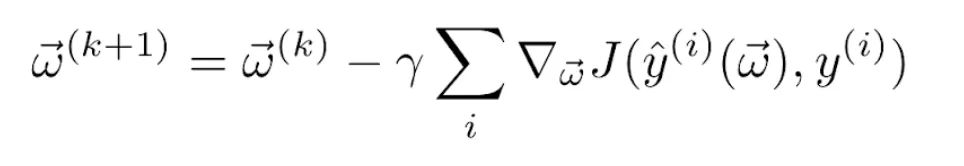
para cada epoch k. En caso de usar la función de pérdidas cuadrática y la función de activación logística como en el ejemplo anterior, tenemos finalmente la actualización de los pesos
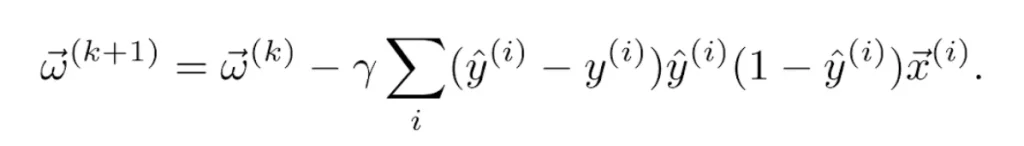
Número de epochs y overfitting
Para terminar, veremos cómo determinar otro hiperparámetro de toda red neuronal, el número de epochs que se deben realizar. De hecho, habitualmente no se fija este número, sino que se establece una regla de parada.
La idea es que el modelo debe ser capaz de aprender la estructura general de los datos de entrenamiento para realizar buenas predicciones. Hay que tener en cuenta que se debe evitar el overfitting (sobreajuste). Es decir, aprender las características particulares de estos datos (como el ruido). De esta manera, se busca que el modelo sea generalizable a conjuntos de datos que no conoce.
Típicamente, un número de epochs demasiado bajo no será suficiente para que el modelo se ajuste a los datos de entrenamiento. Por el contrario, un número muy grande se traducirá en un tiempo de entrenamiento inasumible y probablemente sobreajustará los datos.
Entrenamiento del modelo
Para determinar cuándo debemos parar el entrenamiento, es común usar el siguiente procedimiento. Cuando dividimos el conjunto de datos en entrenamiento y test, subdividimos a su vez el conjunto de entrenamiento y reservamos una parte como conjunto de validación. De esta manera, el modelo se entrena solamente con el resto del conjunto de entrenamiento. Por otra parte, se estudia cómo evoluciona la función de pérdidas (u otras métricas) tanto sobre éste como sobre el conjunto de validación a lo largo del proceso de entrenamiento. Este proceso se realiza habitualmente tras cada actualización de los pesos.
Como el modelo es entrenado con el objetivo de minimizar la función de costes sobre el conjunto de entrenamiento, observaremos en general que el resultado del modelo sobre este conjunto siempre mejora. Sin embargo, es habitual que a partir de cierto número de epochs el resultado empiece a empeorar sobre el conjunto de validación. En este momento, sabremos que se está produciendo overfitting y terminaremos el proceso de entrenamiento (a esto se le llama early stopping). Mientras no se produzca overfitting, podemos seguir con el entrenamiento hasta alcanzar una precisión determinada o un número máximo de epochs predeterminado.
De hecho, en el caso del perceptrón simple, el fenómeno del overfitting es raro. Esto se debe a que el modelo es muy simple y no es capaz de aprender características muy específicas de los datos, siendo más habitual en redes neuronales más complejas como veremos en siguientes posts.
Underfitting y overfitting en la regresión polinómica
Un caso canónico es el de la regresión polinómica. Si elegimos un grado demasiado bajo, el modelo no será suficientemente complejo como para entender la distribución de los datos (a esto también se le llama underfitting). Sin embargo, si el grado es demasiado alto, el modelo aprenderá las características específicas del conjunto de entrenamiento, incluyendo el ruido, y no será generalizable.
La Figura 4 muestra un ejemplo de underfitting y de overfitting en el caso de la regresión polinómica.
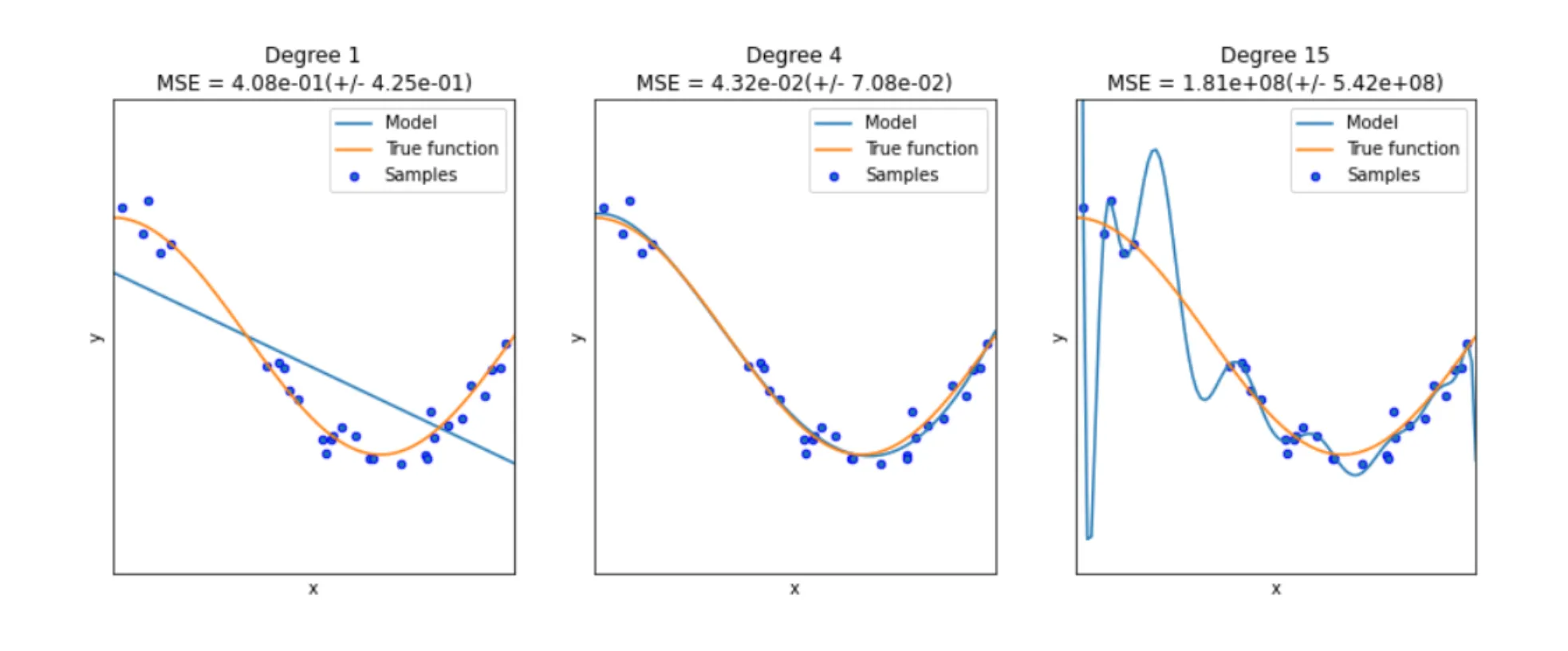
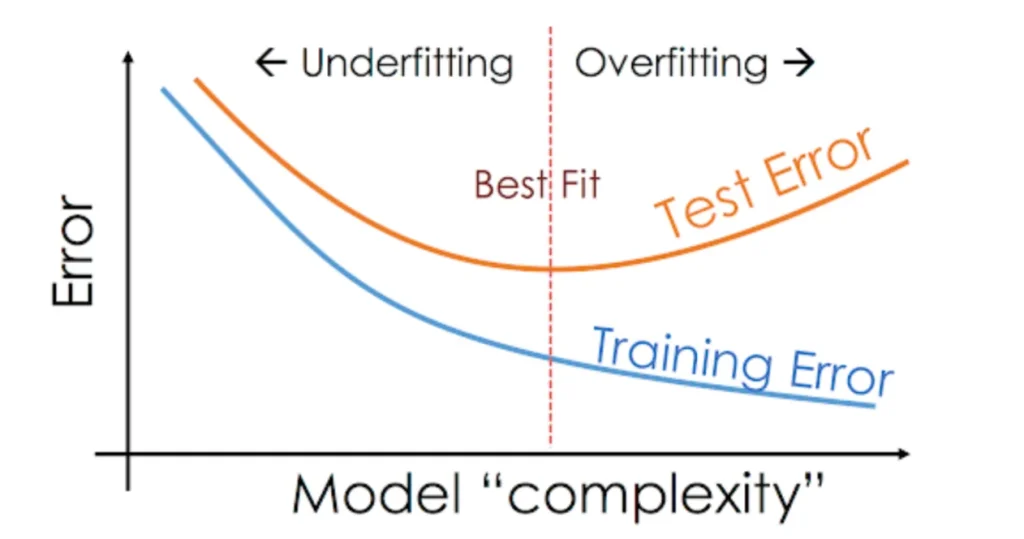
En términos de la complejidad del modelo, la Figura 5 muestra el balance entre tener un modelo demasiado simple o demasiado complejo. En el caso de redes neuronales, una vez fijados los hiperparámetros del modelo (y, por tanto, su complejidad), existe el mismo balance en el número de epochs que se realizan.
Si no se realizan suficientes epochs, el modelo no será capaz de aprender la estructura de los datos. En este caso, el error cometido tanto sobre el conjunto de entrenamiento como sobre el de validación o test, es relativamente alto (todavía tiene margen de mejora).
Sobreentrenamiento del modelo
Si, por el contrario, se sobreentrena el modelo (demasiadas epochs), el modelo cometerá cada vez un error menor sobre el conjunto de entrenamiento. No obstante, perderá capacidad de generalización y dará peores resultados para conjuntos de datos con los que no se haya entrenado, como el de validación o el de test.
Conclusión
Como hemos visto, para un modelo tan sencillo como el perceptrón simple, existen variantes como la elección de la función de pérdidas y de la función de activación, o el criterio de parada. Por supuesto, como en todo proyecto de ciencia de datos, también es importante un buen preprocesado de los datos de entrada, incluyendo su limpieza y normalización.
Te invitamos a seguir con nuestro siguiente post El Perceptrón Simple: Implementación en Python un ejemplo de implementación en Python de este algoritmo, donde estudiamos cómo pueden combinarse distintos perceptrones simples formando redes neuronales artificiales, con un proceso de aprendizaje similar al que hemos descrito aquí, pero más complejo.
Si te ha parecido útil este post, te animamos a ver más artículos como este en la categoría Algoritmos del Blog de Damavis y a compartirlo con tus contactos para que ellos también puedan leerlo y opinar. ¡Nos vemos en redes!