El modelo de regresión lineal es una de las herramientas más útiles en el maletín de utensilios de todo científico de datos. Aunque este post está orientado a personas que conozcan de primera mano este modelo estadístico, nunca está de más recordar que en la regresión lineal se pretende predecir una variable cuantitativa respuesta y (también conocida como variable dependiente) como una combinación lineal de un conjunto de predictores x1, x2, …, xk (también conocidas como variables independientes, variables explicativas o predictores).
Con esta motivación, el modelo de regresión lineal introduce una serie de coeficientes o parámetros poblacionales que representan la relación de cada predictor con la variable respuesta, dando lugar a la clásica ecuación que todos hemos visto alguna vez representada.
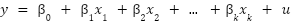
Estos parámetros poblacionales son estimados a partir de un conjunto de datos, utilizando el método de los mínimos cuadrados ordinarios (MCO), el cual garantiza bajo un conjunto de supuestos (supuestos de Gauss-Markov) que los estimadores estadísticos de dichos parámetros son insesgados. Entre estos supuestos, se puede encontrar uno conocido como adicional, el supuesto de homocedasticidad, el cual es necesario para poder realizar inferencia a partir de los coeficientes de la regresión, algo que puede tener mucho valor en determinados contextos.
En este artículo, vamos a hablar sobre este último supuesto adicional, comentando el impacto que puede tener incumplirlo a la hora de interpretar los coeficientes de una regresión, aportando herramientas para detectar si se está cumpliendo este supuesto y ofreciendo soluciones para solventar casos de uso reales en los que dicho supuesto no se satisfaga.
Antes de proceder con la lectura del artículo, se recomienda echarle un vistazo al apéndice definido al final de este, ya que contiene varias definiciones que serán esenciales para poder seguir y comprender todo el contenido a desarrollar.
¿Qué es la heterocedasticidad?
En la ecuación de la regresión lineal presentada en la introducción, se puede apreciar un último concepto denominado comúnmente como el término de error no observado, que representa aquellos factores independientes de los predictores que afectan a la variable respuesta y.
Definido este error no observado, decimos que, en el marco de la regresión lineal, un modelo presenta homocedasticidad cuando dado cualquier valor de las variables explicativas la varianza del error no observado permanece constante. Por el lado contrario, hablamos de heterocedasticidad cuando la varianza del error no observable varía para diferentes segmentos de la población, donde dichos segmentos quedan caracterizados por valores diferentes en los predictores.
Un escenario sencillo en el que se puede observar este fenómeno es en un modelo de regresión lineal simple en el que se pretende modelar el precio de la vivienda en función de una única variable explicativa: la superficie en metros cuadrados. Como podemos observar en la siguiente gráfica, se ve claramente cómo la varianza de los errores con respecto a la regresión ajustada no es constante, siendo notablemente mayor para aquellos casos en los que la superficie es mayor.
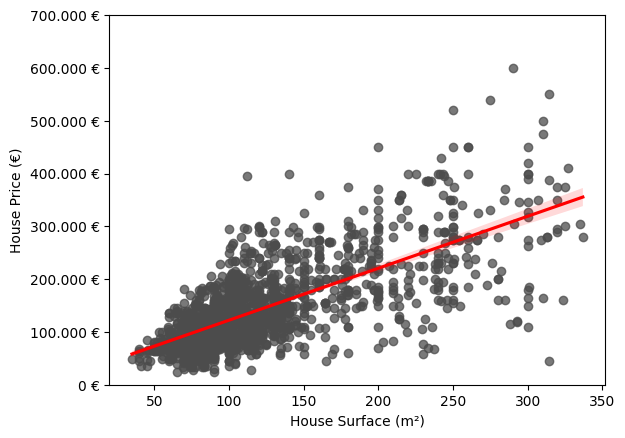
Impacto de la heterocedasticidad en la regresión lineal
Esta heterocedasticidad puede tener un gran impacto en las inferencias realizadas a partir de nuestra regresión. Esto se debe principalmente al supuesto adicional que comentamos en la introducción para estimar los parámetros poblacionales del modelo con MCO, que establece que el modelo no debe mostrar heterocedasticidad. En otras palabras, se requiere que la varianza del error no observado permanezca constante con respecto a las variables explicativas. Ahora, ¿a qué se debe que sea necesario este supuesto? ¿Qué implicaciones conlleva no satisfacerlo?
Conocer por qué son necesarios los supuestos de la regresión lineal no es una tarea trivial y queda fuera del punto de mira de este post, pero aún así se van a dar un par de pinceladas para que el lector pueda cuantificar la importancia de respetar el supuesto de varianza constante del error no observado.
Hasta ahora, hemos denominado este supuesto como un supuesto adicional y esto se debe a que el supuesto de homocedasticidad no es necesario para concluir que los estimadores producidos por el método MCO son insesgados. En este punto, alguno se estará preguntando lo siguiente: Si la heterocedasticidad no causa sesgo ni inconsistencia en los estimadores de MCO, ¿por qué se introduce como supuesto? En resumen, este supuesto nos aporta varios beneficios con respecto a los que son estrictamente necesarios para demostrar que los estimadores MCO son insesgados:
- Al imponer este supuesto se simplifica bastante el desarrollo matemático necesario para aplicar el método de MCO.
- El método MCO adquiere una importante propiedad de eficiencia, es decir, la varianza de los estimadores de los parámetros poblacionales es menor al introducir este supuesto.
- Nos permite definir estimadores insesgados de la varianza de muestreo de los estimadores de los parámetros poblacionales.
De estos tres beneficios, el más importante es el último comentado, ya que sin el supuesto de heterocedasticidad los estimadores de las varianzas son sesgados. Los errores estándar de los parámetros estimados mediante MCO se basan directamente en esta varianza, por lo que si no se satisface este supuesto, estos errores dejan de ser válidos para la construcción de intervalos de confianza y de estadísticos empleados en las pruebas de hipótesis clásicas. Como conclusión final, este supuesto es clave de cara a realizar inferencia estadística sobre el modelo poblacional subyacente a partir de una muestra de datos, ya que la inferencia usual de MCO es incorrecta en presencia de heterocedasticidad.
¿Cómo detectar si existe heterocedasticidad?
Aunque, como hemos visto, la heterocedasticidad puede ser un problema, existen varios test estadísticos que nos permiten detectarla de forma sencilla. En este post, se va a ver una de estas pruebas en detalle, mostrando los fundamentos en los que se basa.
Prueba de Breusch-Pagan
La prueba de Breusch-Pagan para heterocedasticidad surge de la idea de plantear la hipótesis nula (la varianza del error es constante dados los valores de las variables explicativas) como un nuevo ajuste de regresión. Este nuevo modelo de regresión contempla el error no observado al cuadrado como variable dependiente, y las mismas variables explicativas que el modelo original. De esta forma, se puede representar la hipótesis a rechazar previamente planteada como lo siguiente:
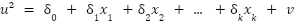
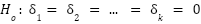
Nunca conoceremos los errores reales del modelo poblacional subyacente, pero sí que podemos obtener una buena estimación de ellos a partir de los residuales de MCO. Por último, mencionar que el estadístico LM a utilizar para poner a prueba la hipótesis vendrá especificado por el tamaño de la muestra y por la bondad del ajuste del modelo que tiene los residuales al cuadrado como variable dependiente.
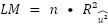
En resumen, el procedimiento para llevar a cabo esta prueba es el siguiente:
- Estimar el modelo de regresión por MCO de forma normal, de cara a obtener los residuales cuadrados.
- Ajustar la regresión en la que la variable independiente son los residuales cuadrados previamente obtenidos y las variables explicativas son las mismas que las del modelo original.
- Calcular el R-cuadrado de esta segunda regresión.
- Calcular el estadístico a partir de la multiplicación del tamaño de la muestra y el R-cuadrado previamente obtenido.
- Usando la distribución Xi con tantos grados de libertad como variables explicativas tenga el modelo, calcular el p-valor de cara a determinar si con un nivel de significancia elegido se rechaza la hipótesis nula de homocedasticidad previamente planteada.
Otras pruebas para la heterocedasticidad
Como bien hemos mencionado, existen otras pruebas que nos permiten detectar la heterocedasticidad. En estos casos, solo se mencionan sus nombres para dar la capacidad al lector de investigar más en detalle las diferencias que contemplan entre ellas:
- Prueba de White
- Prueba de Bartlett
- Prueba de Goldfeld-Quandt
- Prueba de Park
Soluciones al problema de la heterocedasticidad
Existen varios caminos para solventar este problema cuando se pretende hacer inferencia. En este post, se van a plantear tres posibles soluciones, describiendo de forma resumida en lo que consisten.
Inferencia robusta
Pese a que en presencia de heterocedasticidad la inferencia clásica utilizando la estimación por MCO es inválida, esto no implica que la estimación por MCO sea inútil de cara a hacer inferencia en este tipo de escenarios. Es posible ajustar los errores estándar y, por extensión, los diferentes estadísticos empleados clásicamente en inferencia, de forma que sean útiles en escenarios en los que exista heterocedasticidad, incluso si no se conoce ni el comportamiento ni la forma de dicha heterocedasticidad. Queda fuera del alcance de este artículo explicar la deducción matemática detrás de estos ajustes, ya que presupone una base bastante fuerte de estadística.
Este error estándar ajustado es conocido como error estándar robusto a la heterocedasticidad, aunque en la literatura también aparece como errores estándar de White, de Huber o de Eicker. A partir de este error estándar robusto, es posible construir un estadístico t y un estadístico F robusto a la heterocedasticidad. La mayoría de paquetes estadísticos disponen de utilidades para calcular la versión robusta de los estadísticos y facilitarle la vida al usuario.
Hay que comentar que estas versiones robustas de los estadísticos solo son aptas para inferencia si el tamaño de la muestra es lo suficientemente grande, ya que con tamaños de muestra pequeños puede ocurrir que sus distribuciones difieran significativamente de la distribución a la que tiende la versión no robusta del estadístico, haciendo que la inferencia no fuese válida. Es por esta razón por la que normalmente se prefieren usar los estadísticos clásicos siempre, exceptuando aquellos escenarios en los que existe evidencia clara de que existe heterocedasticidad.
Ajuste por mínimos cuadrados ponderados
Hay escenarios en los que de antemano conocemos la forma de la heterocedasticidad, por lo que es posible especificar dicha forma y obtener una estimación por el método de los mínimos cuadrados ponderados (MCP). En caso de que la forma de la heterocedasticidad haya sido correctamente especificada, el método MCP es más eficiente que MCO y conduce a estadísticos válidos para hacer inferencia con distribuciones correctas.
Para especificar la heterocedasticidad, se introduce una función h(x) que hace variar la varianza en función de las variables explicativas. Dado esto, podemos, por ejemplo, definir que esta función es equivalente al valor de una de las variables explicativas de nuestro modelo, haciendo que la varianza del error sea proporcional al valor de dicha variable.
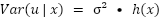
El hecho de introducir una suposición tan fuerte como asumir que se conoce la forma de la heterocedasticidad nos hace plantear la siguiente pregunta: ¿Qué ocurre si se especifica de forma incorrecta dicha forma? En este escenario, se puede asegurar que los estimadores devueltos por MCP siguen siendo insesgados y consistentes, aunque existen dos consecuencias por esta mala especificación:
- El error estándar y los estadísticos dejan de ser válidos para inferencia, incluso en casos en los que el tamaño de muestra es grande. Por suerte, es posible obtener errores estándar robustos a heterocedasticidad arbitraria para MCP de forma similar a como hemos comentado previamente con MCO.
- No existe garantía de que MCP sea más eficiente que MCO. Este hecho aunque teóricamente sea cierto, no tiene una importancia práctica significativa.
Por lo general, en casos en los que existe una fuerte heterocedasticidad, suele ser más conveniente especificar una forma incorrecta de esta y emplear MCP, que ignorar por completo dicha forma y usar MCO.
Transformación de la variable dependiente
Una posible solución más sencilla y práctica para este problema consiste en transformar la variable respuesta y utilizando una función cóncava, como por ejemplo la función logaritmo natural log(y). Este tipo de transformaciones reducen en gran medida aquellos valores de la variable independiente mayores, conllevando una reducción en la heterocedasticidad.
En la siguiente imagen se puede observar cómo quedaría el gráfico mostrado previamente para explicar la heterocedasticidad en el caso de transformar la variable dependiente. Como se puede observar, la varianza de los residuales parece ser más constante de lo que lo era previamente.
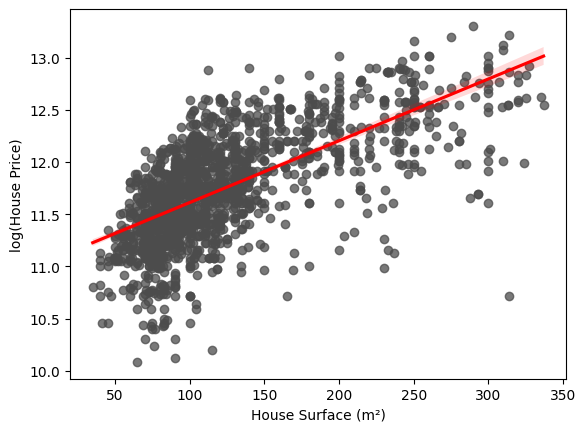
Es importante recalcar que este tipo de transformaciones hacen que la interpretación de los coeficientes de la regresión cambie por completo.
Conclusión
En resumen, la heterocedasticidad es una amenaza a la hora de hacer inferencia estadística a partir de un modelo de regresión lineal ajustado mediante el método de mínimos cuadrados ordinarios. Pese a esto, gracias a este artículo, ahora estás preparado para detectar este fenómeno, y así poder actuar en consecuencia para mitigar su impacto en tu análisis estadístico.
Apéndice
En este apéndice encontrarás varios conceptos relevantes para poder comprender todos los detalles de este post.
Parámetro poblacional: Valor numérico que describe una característica específica de una población estadística completa. Este tipo de valores suelen ser desconocidos, por lo que son estimados a partir de una muestra de la población.
Estimador estadístico: Medida cuantitativa derivada de una muestra de una población utilizada para estimar un parámetro desconocido de dicha población.
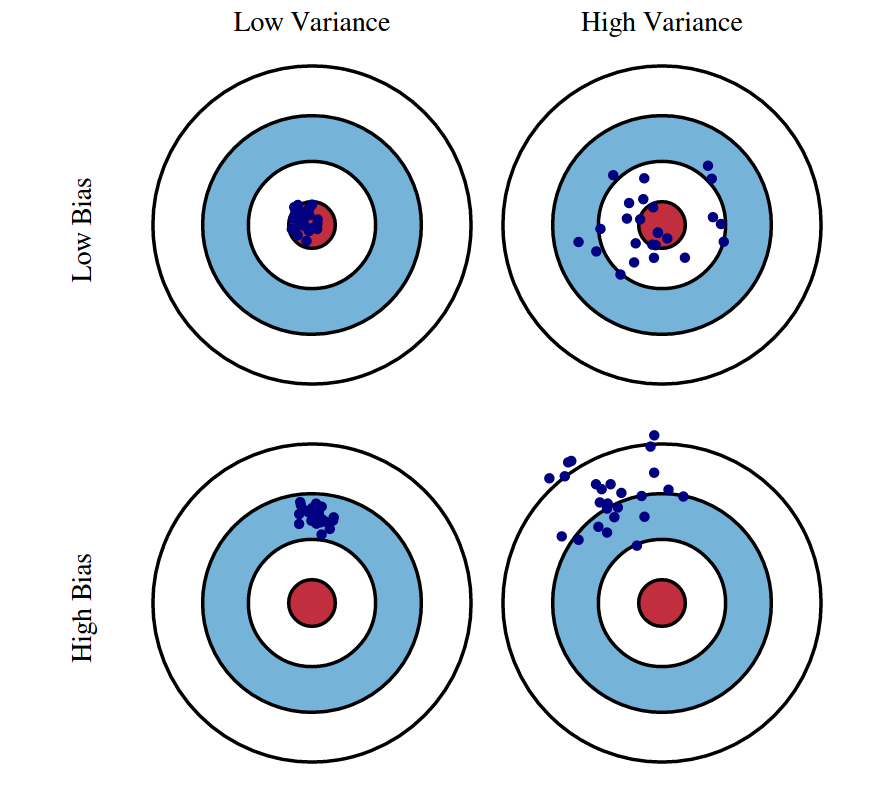
Sesgo: Podemos definir el sesgo como la diferencia entre el promedio o valor esperado de una estimación y el valor real que se pretende estimar. Si un estimador está sesgado, tenderá a sobreestimar o infraestimar un parámetro poblacional de forma sistemática.
Varianza: Medida usada para cuantificar la dispersión de una variable aleatoria con respecto a su valor promedio. En otras palabras, mide en promedio cómo de lejos están los valores de una variable aleatoria de su valor esperado.
Consistencia: Característica de un estimador estadístico que indica que, a medida que aumentamos el tamaño de la muestra utilizada, es cada vez menos probable que el estimador obtenido se aleje mucho del valor real del parámetro poblacional a estimar.
Eficiencia: Dados dos estimadores estadísticos insesgados, se dice que un estimador es más eficiente que otro cuando su varianza es igual o menor para cualquier parámetro poblacional.
