En dos posts anteriores se introdujeron los conceptos básicos de la Lógica Difusa y la programación lineal con el método Simplex. Lo prometido es deuda, en este post vamos a unir estos dos conceptos e introduciremos la programación lineal difusa.
En muchos casos del mundo real, los datos que tenemos no se adecuan a las exigencias de exactitud que marca la implementación de la programación lineal. En este sentido, necesitamos una metodología más flexible que incluya añadir incertidumbre en los datos, es por ello que entra en juego la programación lineal difusa.
Método de Bellman-Zadeh
Vamos a definir lo que son el objetivo, la restricción y la decisión difusos para posteriormente introducir el proceso de toma de decisión de Bellman-Zadeh. Definimos como X el conjunto de todas las posibles alternativas, conteniendo la solución del problema de decisión.
Objetivo difuso: Se define como el conjunto difuso 
sobre X con función de pertenencia 
.
Restricción Difusa: Se define como el conjunto difuso 
sobre X con función de pertenencia 
.
Decisión Difusa: Se define como el conjunto difuso 
sobre X con función de pertenencia 
.
El método de Bellman-Zadeh establece como alternativa óptima 
aquella que maximiza la función de pertenencia de la decisión difusa:
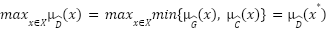
De esta forma, la decisión difusa resuelve el problema de la toma de decisión, ya que para cada alternativa establece el grado con el que se satisfacen las restricciones y el objetivo. El método de Bellman-Zadeh proporciona una alternativa óptima como 
.
Este proceso de toma de decisión se conoce como defusificación.
El objetivo y la restricción difusa tienen el mismo peso sobre la decisión difusa, ninguno tiene un papel más importante que el otro. Es por ello que el método de Bellman-Zadeh es simétrico.
La función de pertenencia que propusieron para la decisión difusa es:
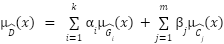
donde 
. Esta definición de la función de pertenencia de la decisión difusa viene motivada porque en ocasiones nos interesa una cierta asimetría en la forma de compatibilizar las restricciones y los objetivos difusos.
Programación lineal difusa simétrica
En muchas ocasiones no queremos optimizar la función objetivo ni que se cumplan de forma estricta las restricciones. En estos casos se quiere alcanzar (o no superar) un cierto nivel fijado como objetivo, de la misma forma que hay cierto grado de flexibilidad respecto a las restricciones. Para estos casos planteamos una variante de los problemas de programación lineal.
Una definición formal de un Problema de optimización de programación lineal difusa simétrica es:
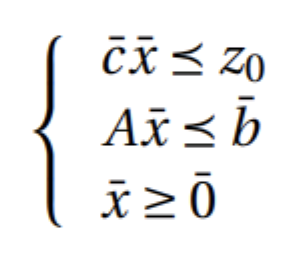
El símbolo 
es una versión difusa de la relación de orden 
y se podría definir como “esencialmente más pequeño o igual que”. Dado que para Bellman y Zadeh los objetivos y restricciones difusos tienen la misma importancia, Zimmermann expresó el problema de la siguiente forma, llamándolo Problema de optimización de programación lineal difusa simétrica de Zimmermann:
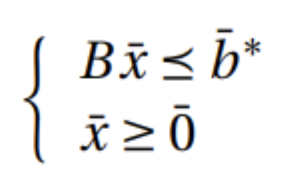
Para poder conectar los problemas de programación lineal difusa con los de programación lineal clásica, Zimmermann consideró que las funciones de pertenencia de cada restricción fuese un número difuso trapezoidal por la derecha:
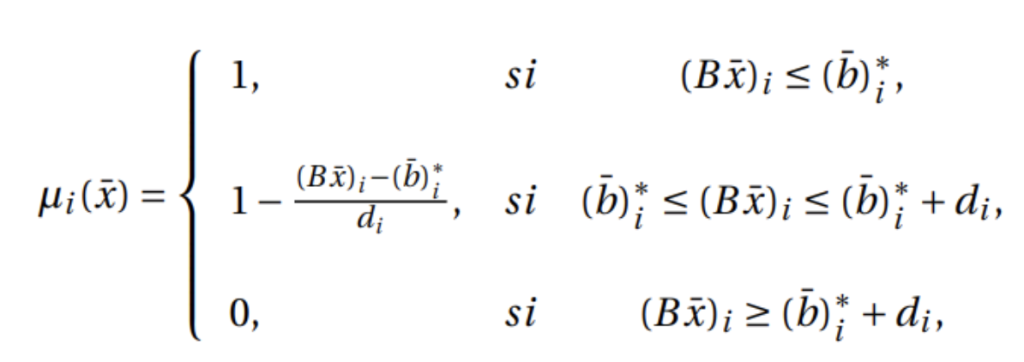
siendo 
una constante que es escoge de forma subjetiva indicando el grado en el que la restricción i-ésima puede ser sobrepasada; 
indica el grado con el que cada 
cumple con la restricción i-ésima.
Recordemos que queremos resolver el siguiente problema: 
. Si añadimos una nueva variable 
podemos plantear el problema como uno de programación lineal clásica:
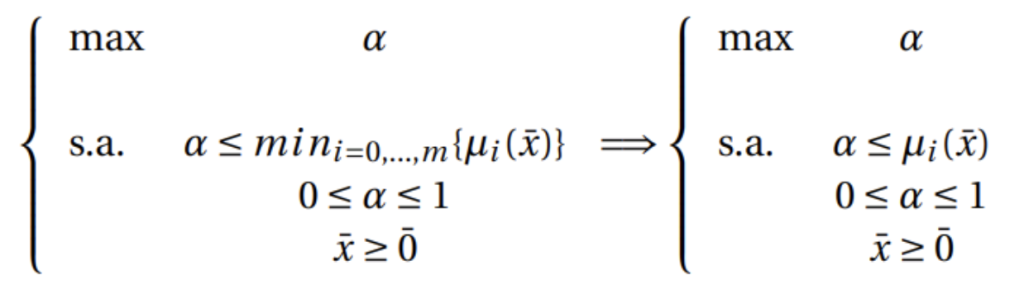
Si consideramos la función de pertenencia que propuso Zimmermann (trapezoidal por la derecha), tendríamos el siguiente problema:
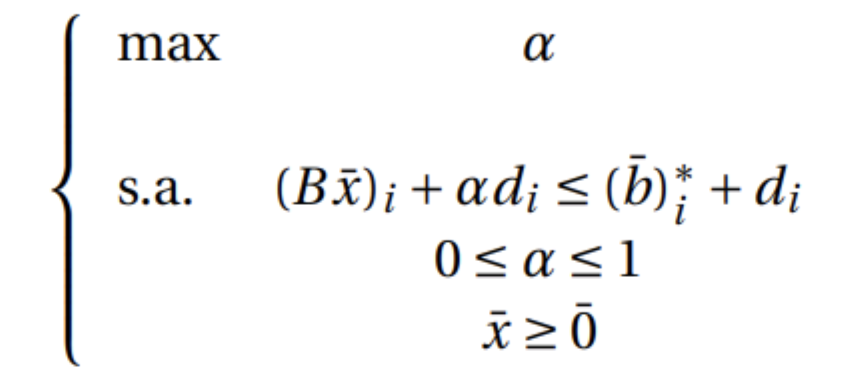
Si 
es el vector de la solución óptima, 
es la solución que maximiza con un grado de pertenencia 
.
Ejemplo práctico
Vamos a poner un ejemplo de cómo podemos tratar un problema de optimización con datos no exactos usando la programación lineal difusa. Para ello, primero consideremos el siguiente problema de optimización:
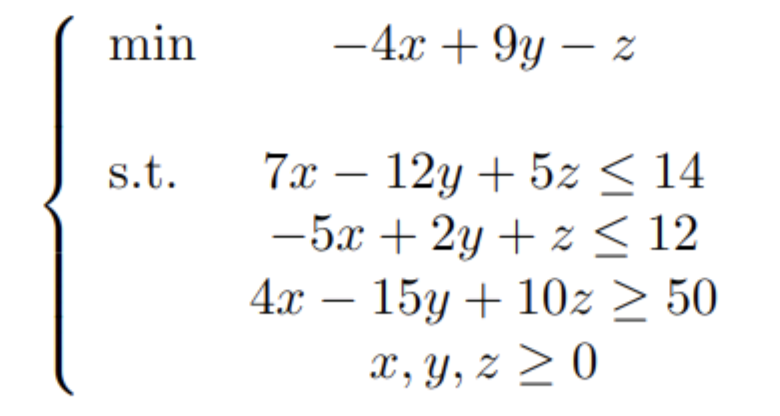
Como vimos en el post de optimización lineal, cambiaremos las restricciones del tipo 
por las del tipo 
simplemente alterando el signo de los números, por comodidad para el planteamiento del problema difuso:
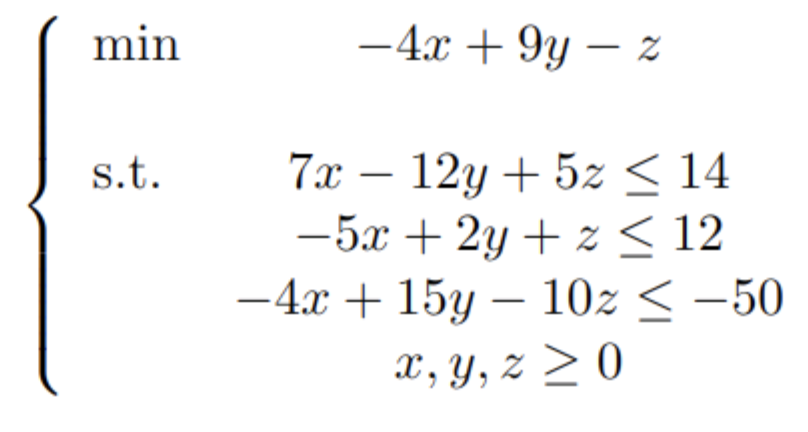
Resolvemos el problema con Python:
from scipy.optimize import linprog
import numpy as np
A_ub = np.array([[7, -12, 5], [-5, 2, 1], [-4, 15, -10]])
b_ub = np.array([14, 12, -50])
c = np.array([-4, 9, -1])
linprog(c=c, A_ub=A_ub, b_ub=b_ub, method="simplex")El resultado que obtenemos es:
message: Optimization terminated successfully.
success: True
status: 0
fun: 18.205882352941185
x: [ 1.029e+00 3.588e+00 9.971e+00]
nit: 3Vemos que el vector de soluciones que obtenemos es 
con valor óptimo 18.21.
Ahora planteamos el problema de manera que haya una cierta flexibilidad en las restricciones y en la función objetivo. Fijamos que el óptimo tiene que ser de al menos 15, entonces el problema original fusificado quedaría de la siguiente manera:
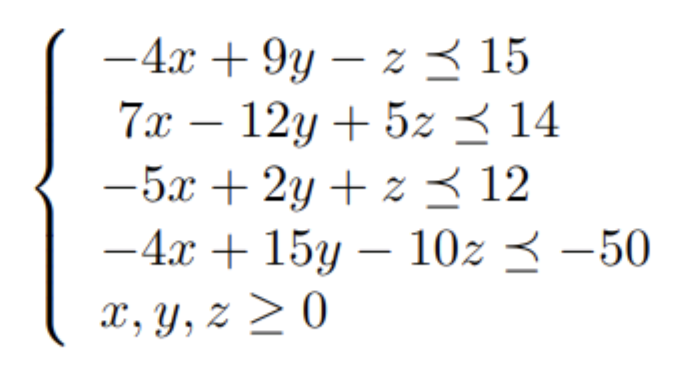
Siguiendo la nomenclatura que Zimmermann introdujo, tenemos:
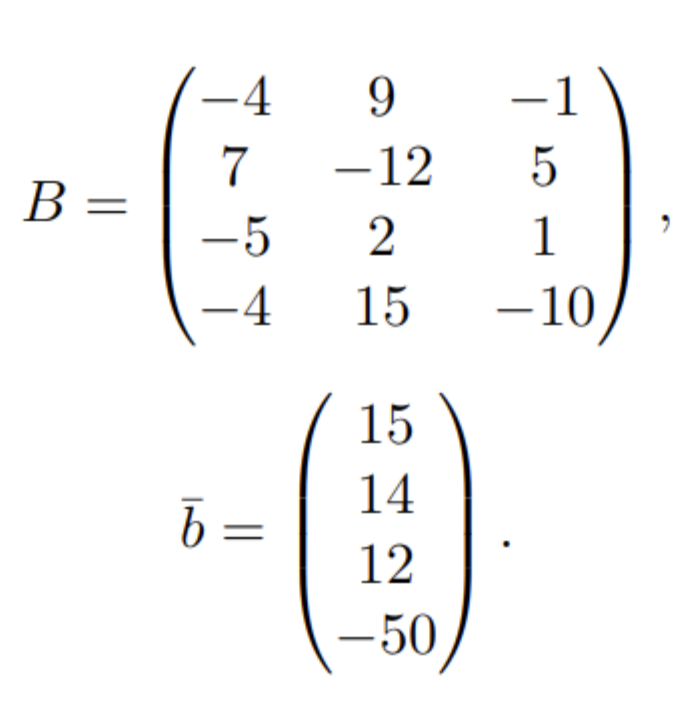
Además, se establecen los siguientes rangos en los cuales cada especificación puede ser transgredido:
- Función objetivo: [15, 18.21]
- Restricción 1: [14, 16]
- Restricción 2: [12, 15]
- Restricción 3: [-50, -48]
Obtenemos de estos rangos los diferentes 
:
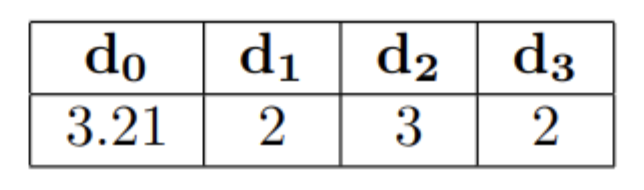
Cada 
corresponde con la amplitud de cada rango proporcionado respecto a las especificaciones del problema. Recordemos que los conjuntos difusos que modelan las especificaciones del problema son trapezoidales por la derecha, vamos a ilustrar la función de pertenencia para la primera especificación y el resto se saca de la misma forma:
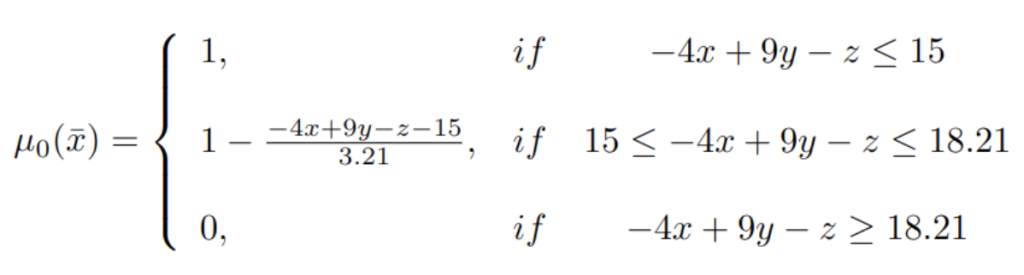
El problema de programación lineal clásica asociado al problema original difuso viene dado por:
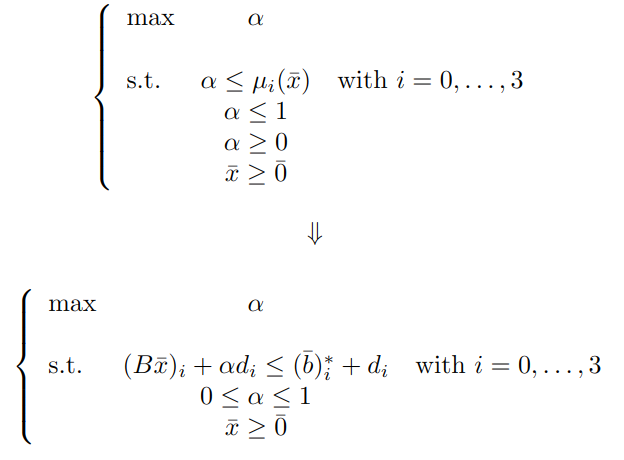
Con las expresiones de las 4 funciones de pertenencia obtenidas y sustituyéndolas, nos sale lo siguiente:
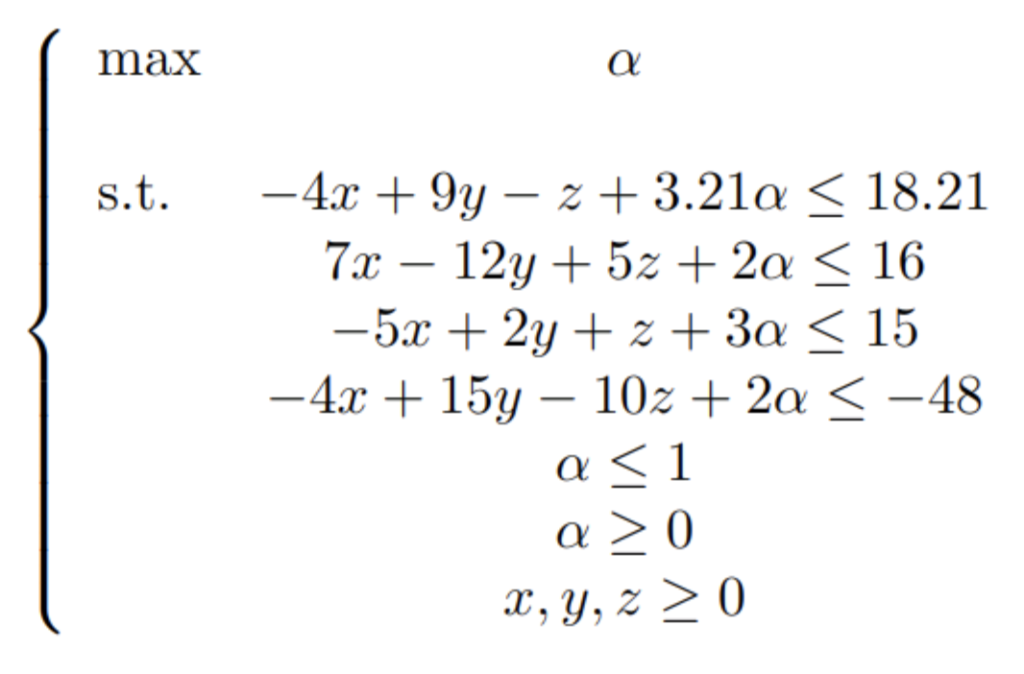
Resolvemos el problema con Python:
from scipy.optimize import linprog
import numpy as np
A_ub = np.array([[-4, 9, -1, 3.21], [7, -12, 5, 2], [-5, 2, 1, 3], [-4, 15, -10, 2], [0, 0, 0, 1]])
b_ub = np.array([18.21, 16, 15, -48, 1])
c = np.array([0, 0, 0, -1])
linprog(c=c, A_ub=A_ub, b_ub=b_ub, method="simplex")Obtenemos el siguiente resultado:
message: Optimization terminated successfully.
success: True
status: 0
fun: -0.8734970521331415
x: [ 5.662e-01 2.989e+00 9.232e+00 8.735e-01]
nit: 5Vemos que el vector de solución que obtenemos es 
con un valor óptimo de 15.4, que está por debajo de los 18.21 que obtuvimos con el problema de optimización lineal clásica. El valor de indica que el problema admite solución con las nuevas consideraciones con un grado de compatibilidad de todas ellas de 0.87.
Conclusión
El objetivo de este post ha sido el unir la lógica difusa con la programación lineal clásica, dando lugar a la programación lineal difusa. El hecho de flexibilizar algunas exigencias que impone la programación lineal nos puede dar mejores resultados, como hemos visto con el ejemplo práctico.
Bibliografía
[1] Masatoshi Sakawa, Hitoshi Yano, Ichiro Nishizaki, and Ichiro Nishizaki. Linear and multiobjective programming with fuzzy stochastic extensions. Springer, 2013.
[2] Hans-Jürgen Zimmermann. Fuzzy set theory—and its applications. Springer Science & Business Media, 2011.
[3] Hans-Jürgen Zimmermann. Fuzzy sets, decision making, and expert systems, volume 10. Springer Science & Business Media, 2012.
