En un post anterior, hablamos sobre los aspectos básicos de la programación lineal y el método Simplex y, en este artículo, vamos a hacer una introducción sobre una rama emergente de las matemáticas: Lógica Difusa. En un artículo posterior, combinaremos la lógica difusa con la programación lineal para la resolución de problemas, donde la mayoría de veces no se tienen datos exactos para poder utilizar la programación lineal.
Empezaremos por definir los conceptos básicos para familiarizarnos e introduciremos los números difusos y 3 tipos diferentes de éstos.
Conjuntos Difusos
Antes de dar una definición de los conjuntos difusos es importante definir la noción de función característica.
Función Característica: Sea
un conjunto y 
, los elementos del subconjunto
pueden ser clasificados mediante una asignación de pertenencia que nos da la función característica:
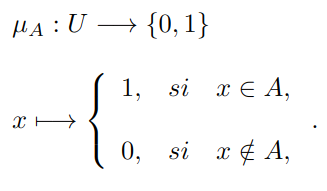
Veamos un ejemplo que ilustre mejor la idea. Si consideramos el conjunto 
como “todas las personas del mundo” y un subconjunto de como “todas las personas delgadas”. Al ser un ejemplo ilustrativo y un tema subjetivo, consideraremos casi de forma aleatoria que las personas delgadas son aquellas que pesen 50 kg o menos. Entonces tenemos nuestra función característica de :
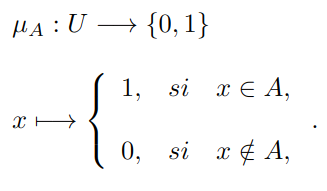
siendo x el peso de la persona que estamos tratando en cuestión. Podemos identificar el conjunto como el siguiente 
.
Tomando únicamente el peso como referencia, esta función característica es un mal instrumento para definir si una persona pertenece o no al conjunto de las personas delgadas. ¿Qué pasa si una persona pesa 49 kg? ¿Y para una persona que pesa 51 kg? La característica para clasificar en estos casos es imprecisa y los valores absolutos como son 0 y 1 no son los mejores para clasificar elementos con un criterio relativo.
Para poder tratar mejor este tipo de información, definiremos lo que es un conjunto difuso y la función de pertenencia multivaluada.
Conjunto Difuso: Sea un conjunto y , el conjunto difuso sobre es el conjunto de pares 
, donde 
es la función de pertenencia multivaluada que nos indica el grado de pertenencia que tiene cada elemento 
al conjunto .
Un conjunto difuso está representado por su función de pertenencia, se refleja el nivel de pertenencia de un elemento respecto de una propiedad que estamos evaluando. Sigamos el ejemplo anterior para ilustrar el concepto introducido cambiando la función de pertenencia:
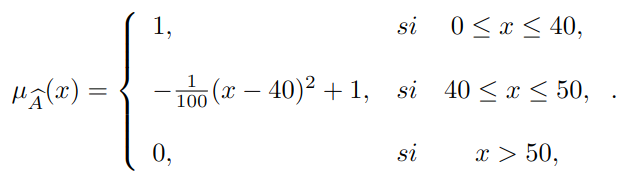
Indicamos 
el peso de la persona y en qué medida puede ser descrita como “delgada”. El siguiente gráfico ilustra la función de pertenencia descrita:
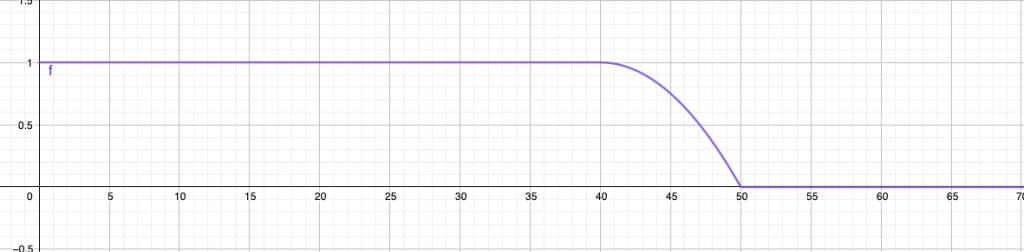
Vemos que una persona que pesa 47 kg (grado de pertenencia 0.51) es menos “delgada” que otra que pesa 43 kg (grado de pertenencia 0.91).
Características de los Conjuntos Difusos
Podemos describir un conjunto difuso mediante sus propiedades, que describen el comportamiento de dicho conjunto.
Consideramos un conjunto , un subconjunto de y el conjunto difuso
correspondiente. Todas las propiedades siguientes son en referencia al conjunto difuso:
- Soporte de
. - Altura de
, donde 
denota el supremo de un conjunto. - Normalidad: es normal si existe
tal que 
. Entonces la altura de es 
.
La normalidad es una propiedad importante a la hora de definir números difusos, pero en muchos casos nuestro conjunto difuso no es normal. Se puede normalizar de una forma sencilla construyendo una nueva función de pertenencia de la siguiente manera:
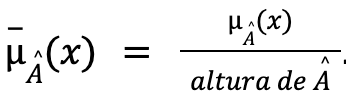
Para ilustrar las características descritas utilizaremos el conjunto difuso del ejemplo anterior con función de pertenencia:
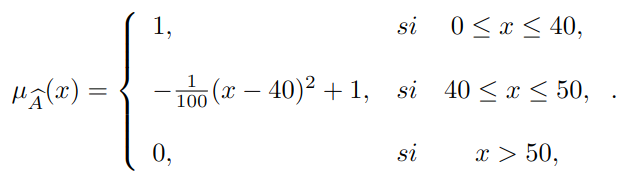
En este caso tenemos:
- Soporte: [0, 50].
- Altura: 1
- Todos los elementos con grado de pertenencia 1 (hacen que el conjunto sea normal): [0, 40].
Números Difusos
Para poder trabajar y modelar con información imprecisa (valores de parámetros que no se conocen con exactitud) necesitamos introducir un tipo particular de conjunto difuso: los números difusos. Exigimos propiedades a los conjuntos difusos para asegurarnos su suavidad y es por esto que definimos primero qué es un conjunto difuso convexo.
Conjunto Difuso Convexo: Sea un conjunto difuso sobre
, es convexo si 
verifica:
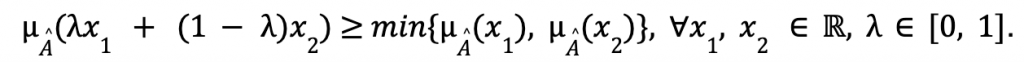
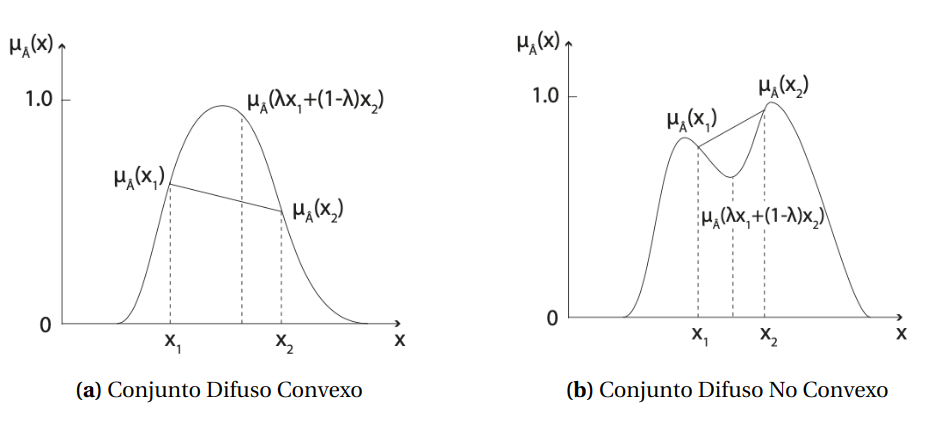
Con todo lo que hemos introducido, ya podemos dar la definición de número difuso.
Número Difuso: Sea un conjunto difuso sobre , es un número difuso si es convexo, normal y su función de pertenencia es continua a trozos.
Un ejemplo de número difuso es el siguiente: consideramos el conjunto difuso sobre cuya función de pertenencia es: 
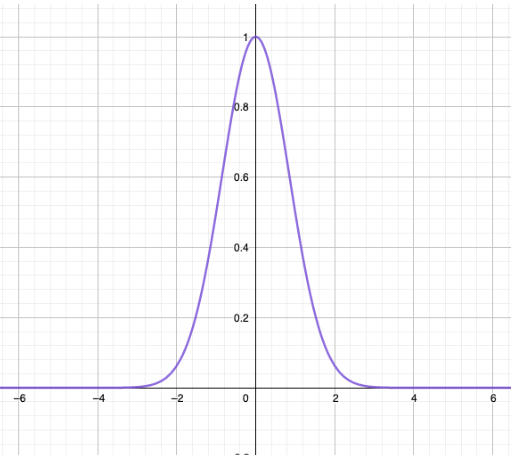
Vemos que este conjunto difuso es convexo, normal ya que 
y es continua y, por tanto, continua a trozos.
Como ejemplo vamos a ver 3 tipos diferentes de números difusos: números difusos acampanado, triangular y trapezoidal.
Número Difuso Acampanado
Un número difuso es un número difuso acampanado o cuadrático a trozos si su función de pertenencia tiene la siguiente forma:
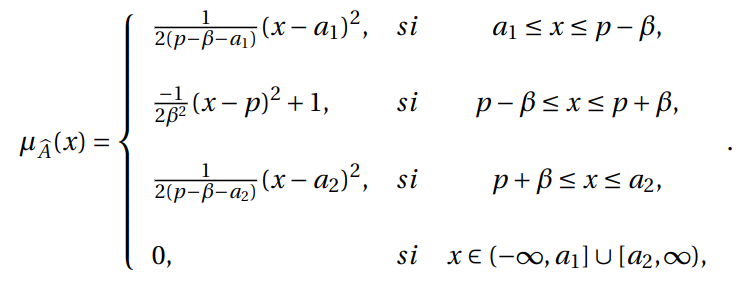
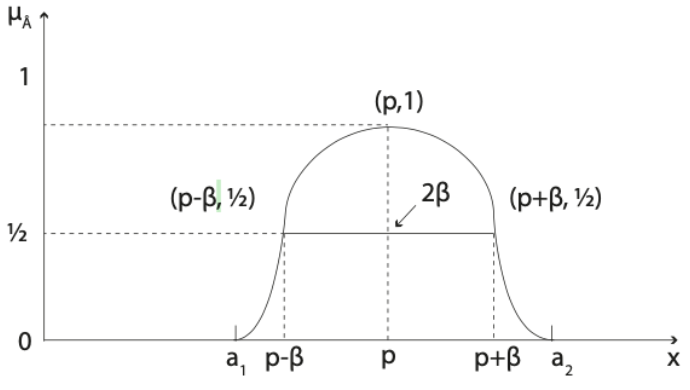
Algunas características que tiene este tipo de número difuso son:
- El soporte es
siendo 
y 
los valores más pequeño y grande respectivamente. 
es el punto medio del segmento 
.- El punto máximo es y el valor máximo es 1.
Número Difuso Triangular
Sea un conjunto difuso sobre, es un número difuso triangular si su función de pertenencia viene dada por:
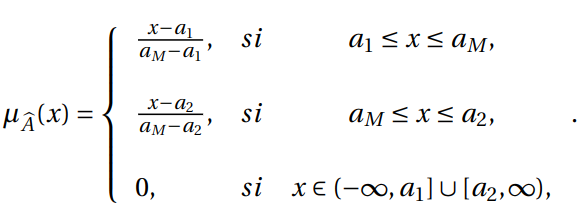
Algunas propiedades son:
- El soporte es
. - El punto máximo es
y el valor máximo es 1. - Son en general asimétricos respecto el eje
.
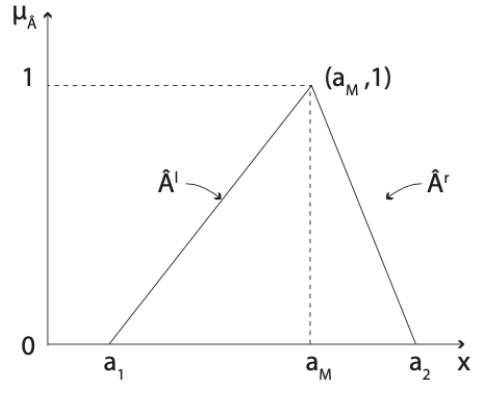
La linealidad a trozos de la función de pertenencia hace que estos números difusos sean muy útiles para aplicarlo en problemas de optimización con información imprecisa y, a su vez, estos problemas pueden ser conectados con la programación lineal.
Número Difuso Trapezoidal
Para el siguiente post en el que conectaremos la lógica difusa con la programación lineal para dar paso a la programación lineal difusa, utilizaremos el siguiente tipo de número difuso.
Un número difuso es un número difuso trapezoidal si su función de pertenencia tiene la siguiente forma:
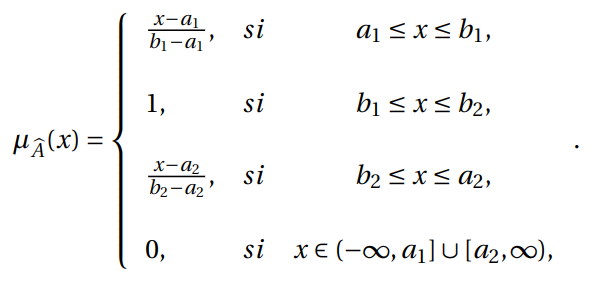
Las propiedades que los caracterizan son:
- El soporte es .
- No existe punto máximo.
- Si
entonces es un número difuso triangular.
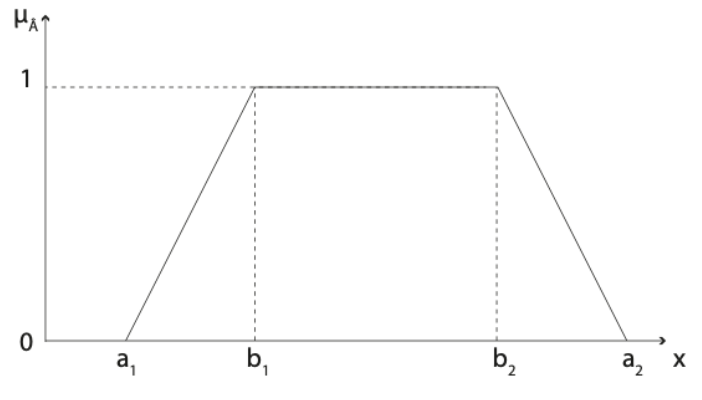
Estos tipos de números difusos permiten describir datos numéricos en aquellas situaciones en las que el valor a aproximar se sabe que debe estar acotado en 
. Debido a la imprecisión se permite una tolerancia al error asimétrico que viene dada por los valores y .
Conclusión
En este post hemos dado una pequeña introducción a los aspectos básicos de la lógica difusa como son los conjuntos difusos y sus características y los números difusos. Es una parte teórica y sirve como enlace entre el post de programación lineal y un posterior post sobre una introducción a la Programación Lineal Difusa.
Bibliografía
[1] Masatoshi Sakawa, Hitoshi Yano, Ichiro Nishizaki, and Ichiro Nishizaki. Linear and multiobjective programming with fuzzy stochastic extensions. Springer, 2013.
[2] Hans-Jürgen Zimmermann. Fuzzy set theory—and its applications. Springer Science & Business Media, 2011.
[3] Hans-Jürgen Zimmermann. Fuzzy sets, decision making, and expert systems, volume 10. Springer Science & Business Media, 2012.
