In a previous post, we talked about the basics of linear programming and the Simplex method and, in this article, we are going to give an introduction to an emerging branch of mathematics: Fuzzy Logic. In a later article, we will combine fuzzy logic with linear programming for problem solving, where most of the time we do not have exact data to be able to use linear programming.
We will start by defining the basic concepts to get familiar with them and we will introduce fuzzy numbers and 3 different types of fuzzy numbers.
Fuzzy Sets
Before giving a definition of fuzzy sets, it is important to define the notion of characteristic function.
Characteristic Function: Let
be a set and
, the elements of the subset 
can be classified by a membership assignment given by the characteristic function:
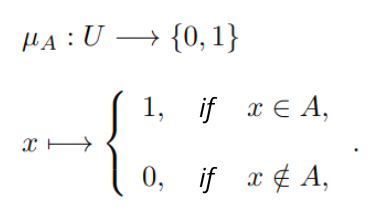
Let’s look at one example to illustrate this idea better. If we consider the set 
as “all people in the world” and a subset of as “all thin people”. Being an illustrative example and a subjective topic, we will consider almost randomly that thin people are those who weigh 50 kg or less. Then we have our characteristic function of :
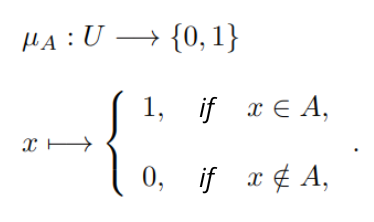
where x is the weight of the person we are dealing with in question. We can identify the set as the following 
.
Taking only weight as a reference, this characteristic function is a bad instrument to define whether or not a person belongs to the set of thin people. What happens if a person weighs 49 kg? And for a person who weighs 51 kg? The characteristic to classify in these cases is imprecise and absolute values such as 0 and 1 are not the best to classify elements with a relative criteria.
In order to better deal with this kind of information, we will define what a fuzzy set is and the multivalued membership function.
Fuzzy Set: Let be a set and , the fuzzy set over is the set of pairs 
, where 
is the multivalued membership function that tells us the level of membership that each element 
has to the set .
A fuzzy set is represented by its membership function, which reflects the level of membership of an element with respect to a property we are evaluating. Following the example above, let’s illustrate the concept introduced by changing the membership function:
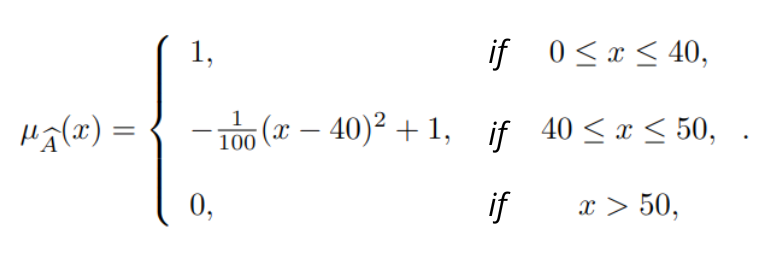
We indicate 
the person’s weight and how much the person can be described as “thin”. The following graph illustrates the described membership function:
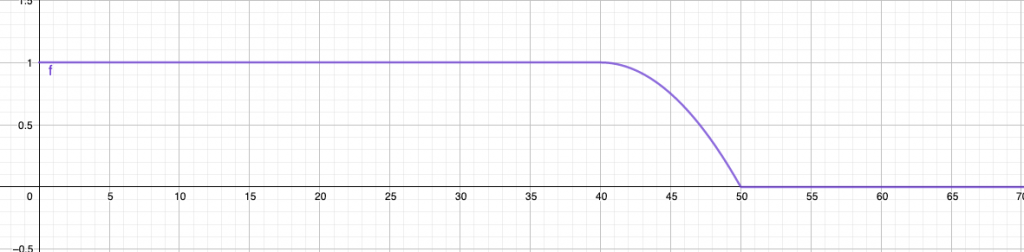
We see that a person weighing 47 kg (membership degree 0.51) is less “thin” than a person weighing 43 kg (membership degree 0.91).
Fuzzy Set Properties
We can describe a fuzzy set by its properties, which describe the behaviour of the fuzzy set.
We consider a set , a subset of , and the corresponding fuzzy set
. All the following properties are in reference to the fuzzy set:
- Support of
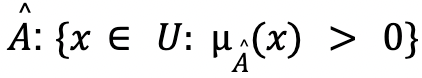. - Height of
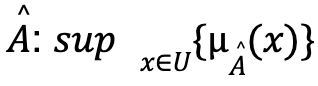, where 
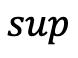denotes the supremum of a set. - Normality: 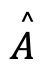is normal if there exists
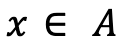such that 
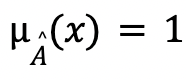. Then the height of 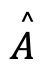is 
.
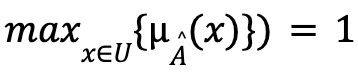Normality is an important property when defining fuzzy numbers, but in many cases our fuzzy set is not normal. It can be normalized in a simple way by constructing a new membership function as follows:
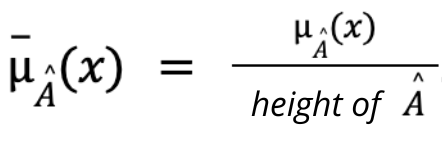
To illustrate the characteristics described above, we will use the fuzzy set of the previous example with membership function:
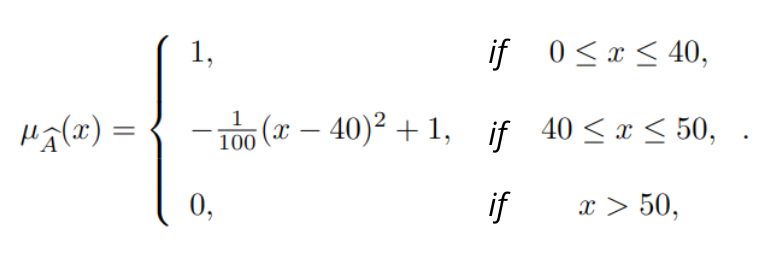
In this case we have:
- Support: [0, 50].
- Height: 1
- All elements with degree of membership 1 (make the set normal): [0, 40].
Fuzzy Numbers
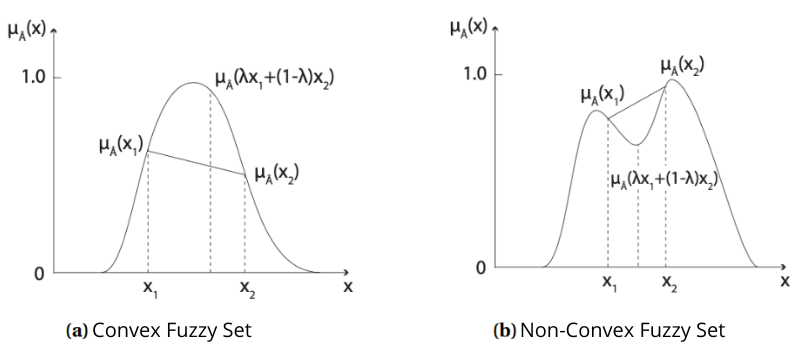
In order to be able to work and model with imprecise information (parameter values that are not known exactly), we need to introduce a particular type of fuzzy set: fuzzy numbers. We require properties of fuzzy sets to ensure their smoothness and this is why we first define what a convex fuzzy set is.
Convex Fuzzy Set: Let be a fuzzy set over 
, is convex if 
be a fuzzy set over , is convex if verifies that:
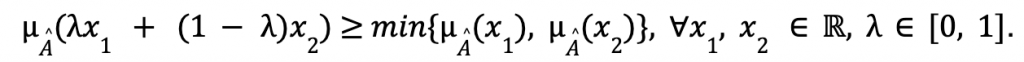
With all that we have introduced, we can now give the definition of a fuzzy number.
Fuzzy Number: Let be a fuzzy set over , is a fuzzy number if it is convex, normal and its membership function is piecewise continuous.
An example of a fuzzy number is the following: consider the fuzzy set over whose membership function is: 
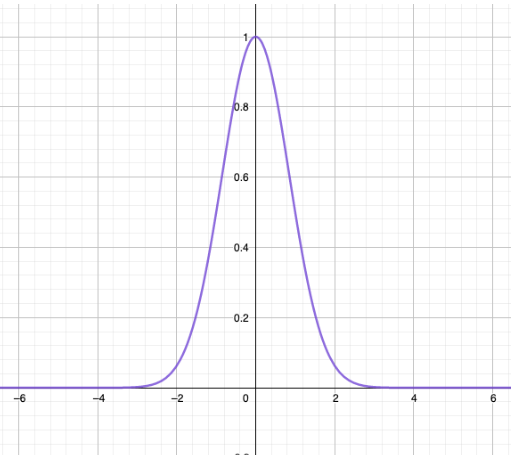
We see that this fuzzy set is convex, normal since 
and is continuous and therefore continues in pieces.
As an example we are going to see 3 different types of fuzzy numbers: flared, triangular and trapezoidal fuzzy numbers.
Bell-shaped Fuzzy Number
A fuzzy number is a flared or piecewise quadratic fuzzy number if its membership function has the following form:
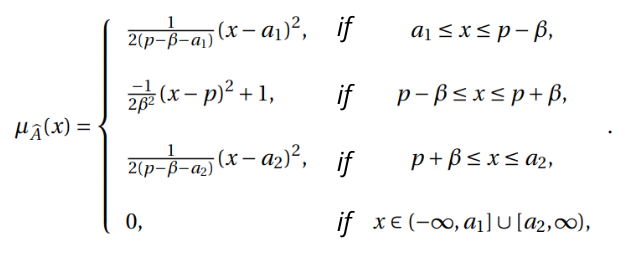
Some characteristics of this type of fuzzy number are:
- The support is
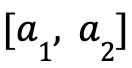, with 
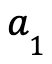and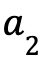 
being the smallest and largest values respectively. 
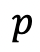is the midpoint of the segment 
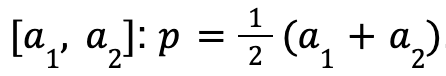.- The maximum point is 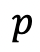and the maximum value is 1.
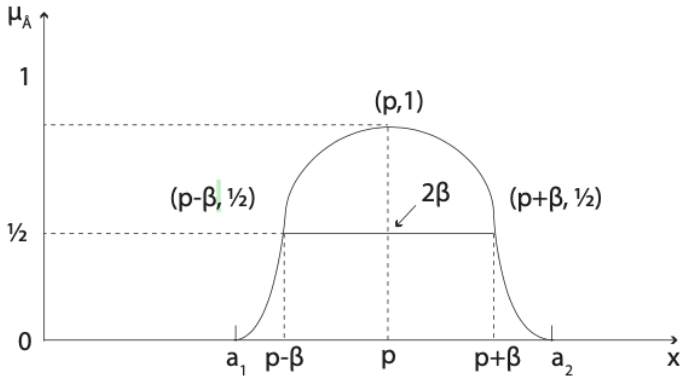
Triangular Fuzzy Number
Let be a fuzzy set over , is a triangular fuzzy number if its membership function is given by:
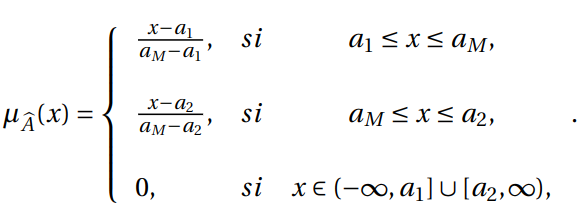
Some properties are:
- The support is
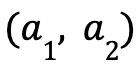. - The maximum point is
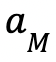and the maximum value is 1. - They are in general asymmetric with respect to the axis
.
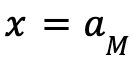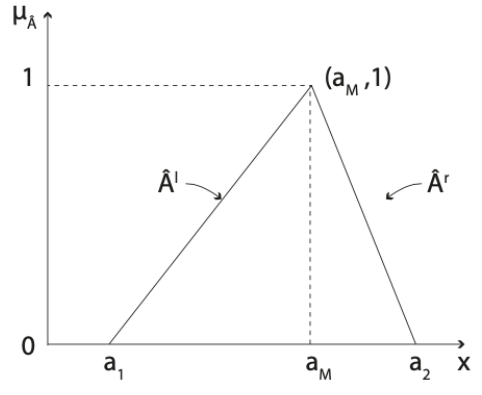
The piecewise linearity of the membership function makes these fuzzy numbers very useful to apply to optimization problems with imprecise information and, at the same time, these problems can be connected to linear programming.
Trapezoidal Fuzzy Number
For the next post in which we will connect fuzzy logic with linear programming to give way to fuzzy linear programming, we will use the following type of fuzzy number.
A fuzzy number is a trapezoidal fuzzy number if its membership function has the following form:
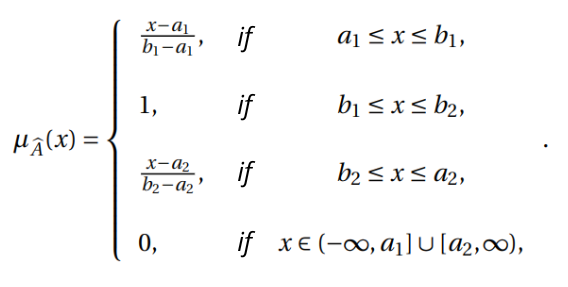
The properties that characterize them are:
- The support is
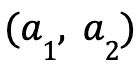. - There is no maximum point.
- If
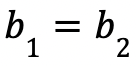, then it is a triangular fuzzy number.
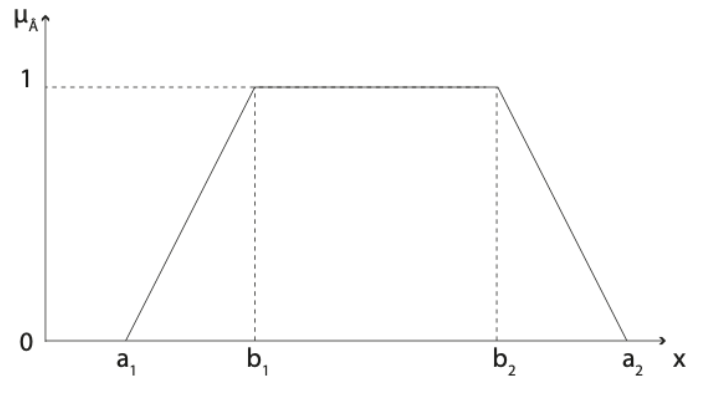
These types of fuzzy numbers allow to describe numerical data in those situations where the value to be approximated is known to be bounded in 
. Due to the imprecision, an asymmetric error tolerance is allowed, which is given by the and values.
Conclusion
In this post we have given a small introduction to the basic aspects of fuzzy logic such as fuzzy sets and their characteristics and fuzzy numbers. It is a theoretical part and serves as a link between the post on linear programming and a later post on an introduction to Fuzzy Linear Programming.
Bibliography
[1] Masatoshi Sakawa, Hitoshi Yano, Ichiro Nishizaki, and Ichiro Nishizaki. Linear and multiobjective programming with fuzzy stochastic extensions. Springer, 2013.
[2] Hans-Jürgen Zimmermann. Fuzzy set theory—and its applications. Springer Science & Business Media, 2011.
[3] Hans-Jürgen Zimmermann. Fuzzy sets, decision making, and expert systems, volume 10. Springer Science & Business Media, 2012.
