Un ejemplo de cómo el uso de grafos puede ayudarnos a encontrar rutas óptimas para solucionar diversos problemas.
Un sistema de grafos puede utilizarse con múltiples finalidades, siendo en algunos casos muy útil para resolver problemas complejos. En esta ocasión vamos a ver cómo utilizar esta herramienta para encontrar caminos óptimos con grafos.
En primer lugar construiremos un grafo dirigido tipo grid de dos dimensiones de 6 x 6 sobre el que trabajar. Además, nos quedaremos con el identificador del primer y último nodo para utilizarlos más adelante.
DG = nx.grid_2d_graph(6, 6, periodic=False).to_directed()
positions = nx.kamada_kawai_layout(DG,)
start_node = list(DG.nodes())[0]
end_node = list(DG.nodes())[-1]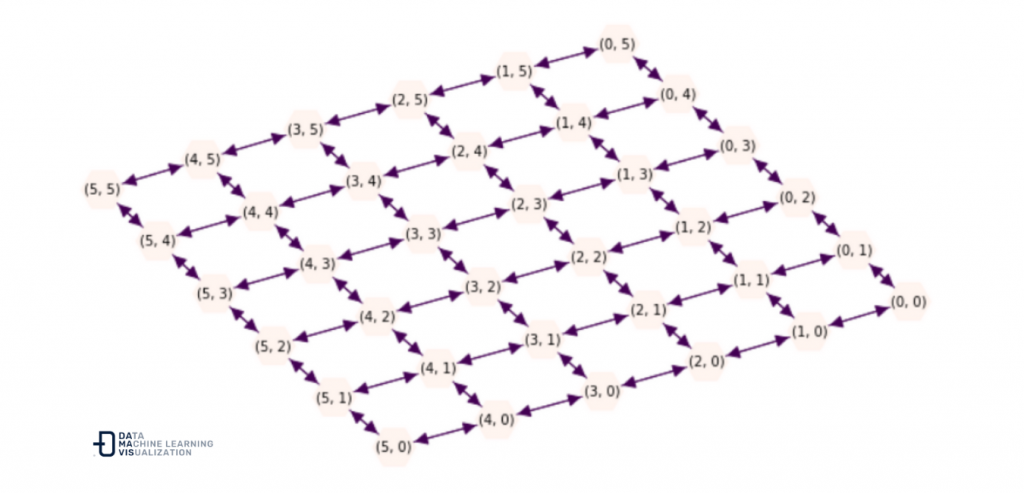
Vamos a hacer un sistema que encuentre el camino óptimo desde el punto inicial (start_node) hasta el punto final (end_node). Pero pondremos un punto de complejidad para hacer el ejercicio más divertido.
Imaginemos que cada uno de los nodos son salas de un edificio en llamas, las cuales tienen distintas temperaturas. Nuestro objetivo es llegar desde el punto inicial hasta la salida pasando por las habitaciones menos calientes.
El siguiente paso entonces, es asignar de forma aleatoria nuestro grafo (salas del edificio), puntos calientes iniciales y puntos calientes colindantes.
hot_nodes = random.choices(list(DG.nodes()), k=5)
DG.add_nodes_from(hot_nodes, node_temp=0.9)
for hot_node in hot_nodes:
this_neighbors = list(DG.neighbors(hot_node))
DG.add_nodes_from(this_neighbors, node_temp=0.5)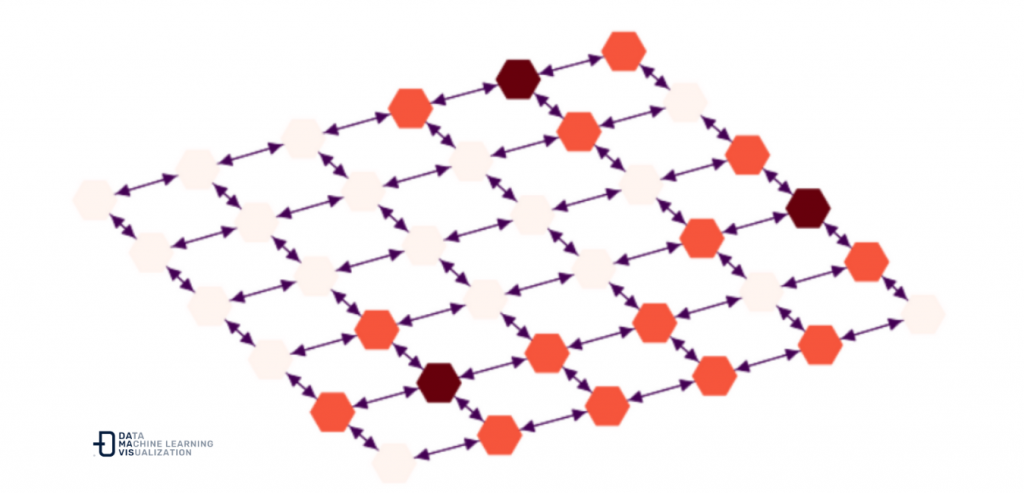
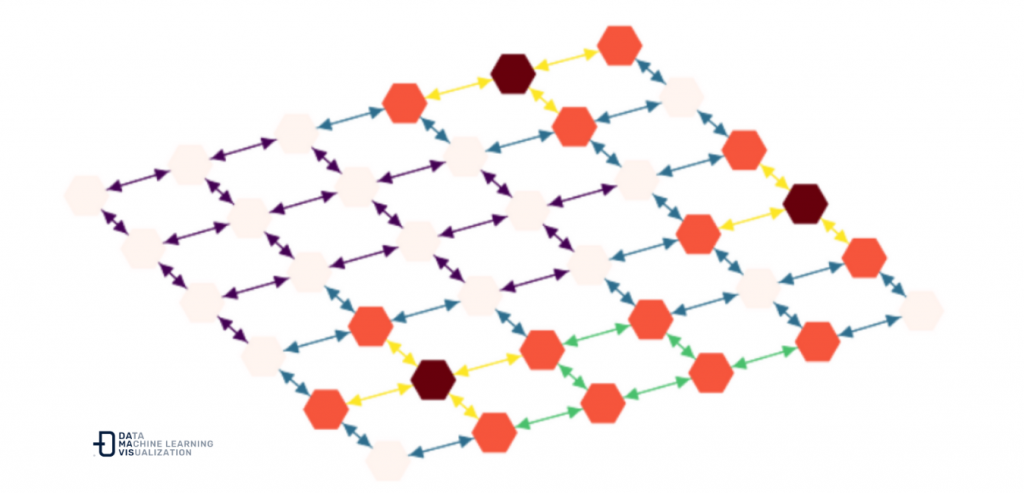
Ahora vamos a tratar con las aristas (pasillos) que conectan entre ellos nuestros nodos (salas). Estos pasillos tendrán una temperatura media obtenida entre la temperatura de las salas que conecta.
De tal manera que, si recorremos cada arista del grafo podemos calcular la temperatura y asignarla de la siguiente forma:
for edge_ori, edge_dest in list(DG.edges()):
DG.add_edges_from(
[(edge_ori, edge_dest)],
edge_temp=np.mean(
[DG.nodes[edge_ori]["node_temp"],
DG.nodes[edge_dest]["node_temp"]]
)
)
Por lo tanto, si lo que queremos es encontrar el camino óptimo desde el punto inicial (en este caso, nodo del extremo derecho) al punto final (nodo del extremo izquierdo), podemos utilizar uno de los algoritmos que resuelve este tipo de problemas siendo óptimos en cuanto a computación.
El algoritmo A*, que tiene un funcionamiento como el que se puede ver en la siguiente imagen.
De este modo, si utilizamos este sistema sin tener en cuenta las temperaturas de los nodos, encontraríamos como respuesta uno (puede haber varios) de los caminos más cortos del punto inicial al punto final.
nx.astar_path(DG, start_node, end_node)
[(0, 0),
(1, 0),
(2, 0),
(3, 0),
(4, 0),
(5, 0),
(5, 1),
(5, 2),
(5, 3),
(5, 4),
(5, 5)]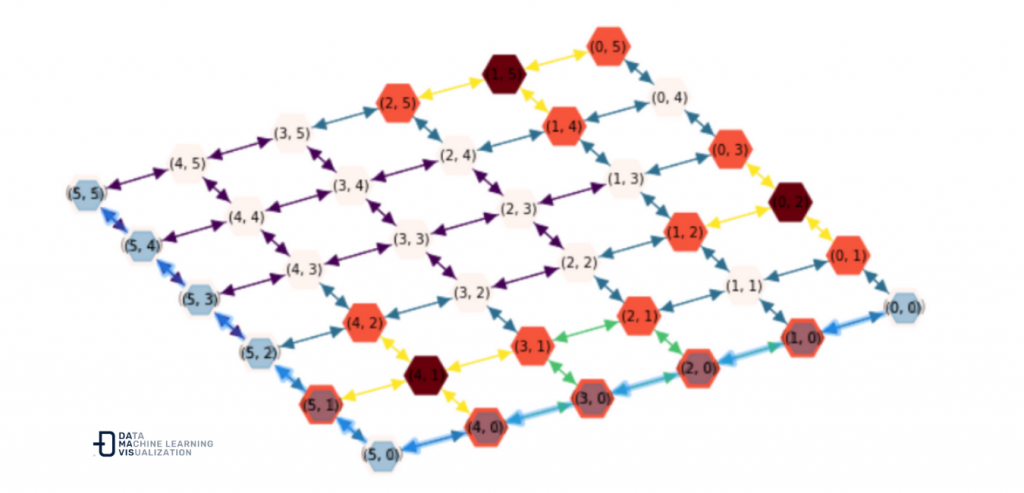
Aunque como hemos dicho, no es esto lo que buscamos, porque si pasásemos por todas las salas que nos indica el camino más corto, pasaríamos por salas y pasillos con unas temperaturas muy altas.
Por ello, repitamos el proceso, esta vez teniendo en cuenta las temperaturas para encontrar el camino más corto y frío posible.
nx.astar_path(DG, start_node, end_node, weight='edge_temp')
[(0, 0),
(1, 0),
(1, 1),
(2, 1),
(2, 2),
(3, 2),
(3, 3),
(4, 3),
(5, 3),
(5, 4),
(5, 5)]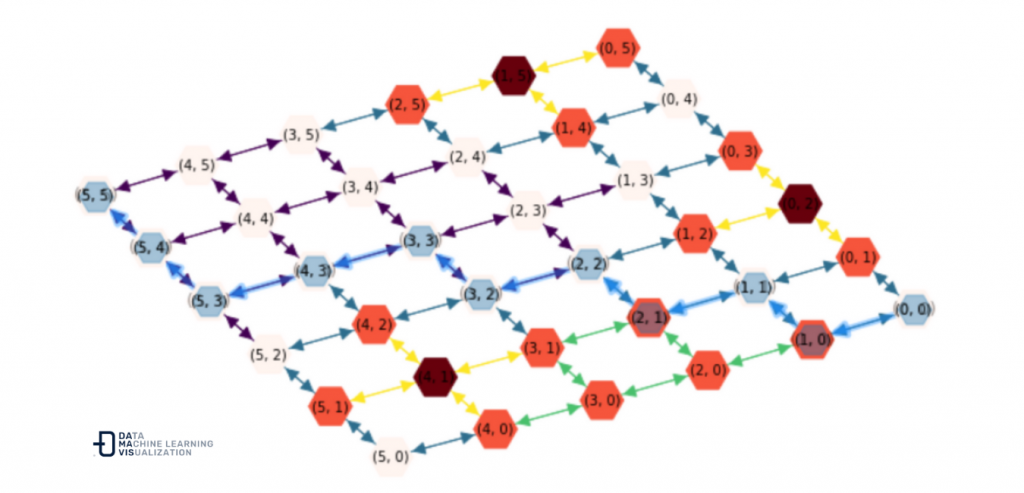
Así tenemos ya un sistema que resuelve el problema que hemos presentado en cuestión de milisegundos.
Sin embargo, ¿qué pasaría si, además, eliminamos algunos nodos de nuestro grafo, simulando salas inaccesibles por el incendio?, por ejemplo:
to_remove = [
(5, 1), (4, 2), (3, 3),
(0, 2), (1, 1), (2, 1)
]
for node in to_remove:
DG.remove_node(node)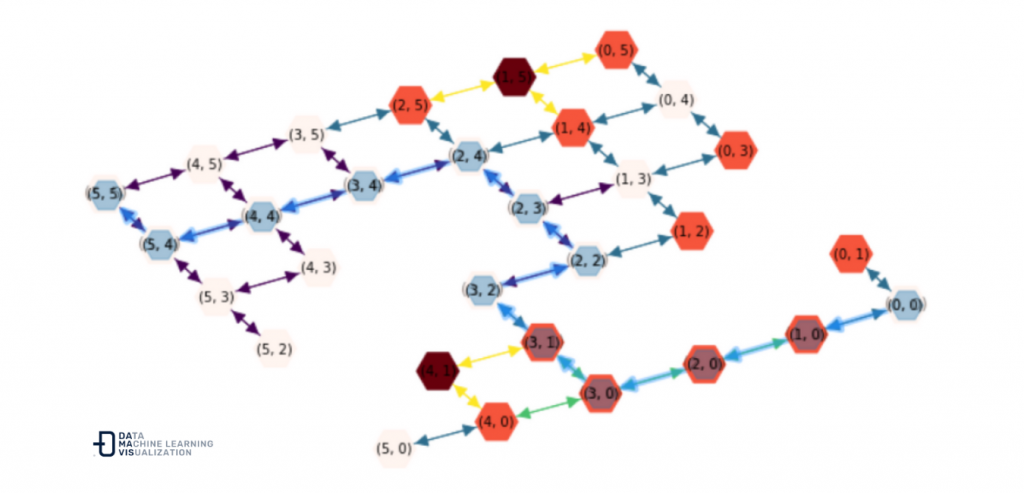
La ruta se adapta al entorno y obtenemos de nuevo el camino más óptimo teniendo en cuenta la temperatura del trayecto.
De esta forma y con el algoritmo ya preparado, podemos generar un entorno mucho más grande y hacer que el algoritmo se enfrente a un número mayor de decisiones a tomar para encontrar la ruta óptima.
Por ejemplo, generando un nuevo grafo de 2500 nodos y 150 puntos de calor a tener en cuenta.
Y con la misma facilidad de lo ya programado, obtenemos la ruta óptima a la salida.
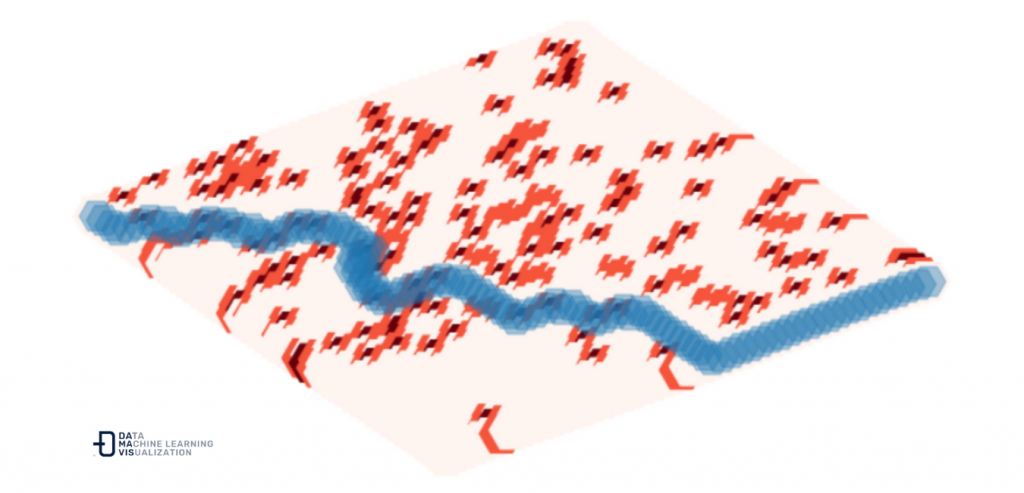
Evidentemente esto es un ejemplo simple explicativo del uso de grafos para explicar cómo pueden utilizarse a la hora de resolver ciertos problemas. Estas mismas herramientas pueden ser útiles para resolver distintas problemáticas que podemos encontrarnos en las empresas en su día a día.
A continuación, algunos ejemplos de distintas complejidades sobre los que se puede trabajar con un sistema de grafos y elección de caminos óptimos:
- Optimización de espacios de almacén
- Distribución de mercancías
- Ahorro de combustible en flotas de vehículos
- Optimización de reglas de compra / venta de productos
El código del ejemplo expuesto está en https://github.com/ para que puedas descargarlo y utilizarlo tú mismo.
