An example of how the use of graphs can help us find optimal routes to solve various problems.
A graph system can be used for multiple purposes, being in some cases very useful to solve complex problems. In this article will show you how to use this tool to find optimal routes with graphs.
First we will build a two-dimensional 6 x 6 directed graph grid to work on. We will also keep the identifier of the first and last node for later use.
DG = nx.grid_2d_graph(6, 6, periodic=False).to_directed()
positions = nx.kamada_kawai_layout(DG,)
start_node = list(DG.nodes())[0]
end_node = list(DG.nodes())[-1]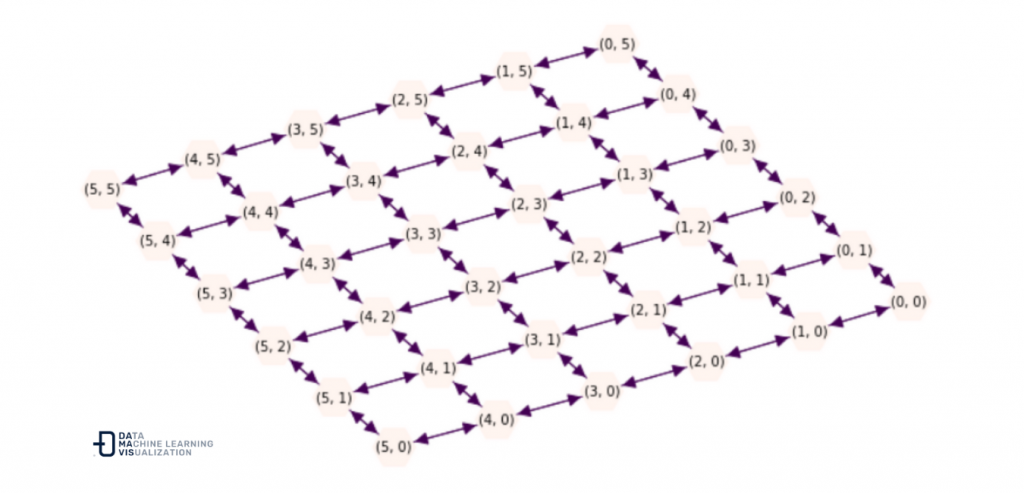
We are going to make a system that finds the optimal route from the initial point (start_node) to the final point (end_node). But we will add a point of complexity to make the exercise more fun.
Let’s imagine that each of the nodes are rooms in a burning building, which have different temperatures. Our goal is to get from the starting point to the exit by getting through the less hot rooms.
So next step, is to randomly assign our network (building rooms), initial hotspots and neighbouring hotspots.
hot_nodes = random.choices(list(DG.nodes()), k=5)
DG.add_nodes_from(hot_nodes, node_temp=0.9)
for hot_node in hot_nodes:
this_neighbors = list(DG.neighbors(hot_node))
DG.add_nodes_from(this_neighbors, node_temp=0.5)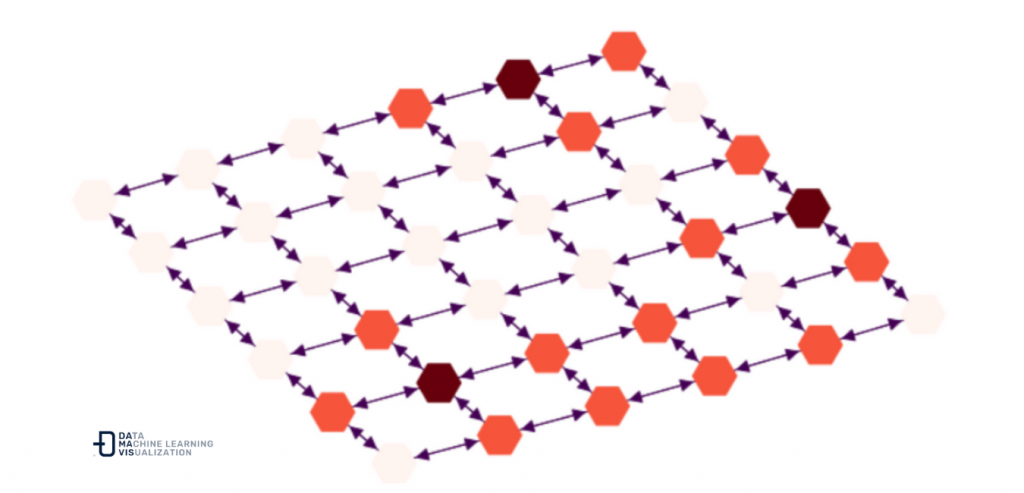
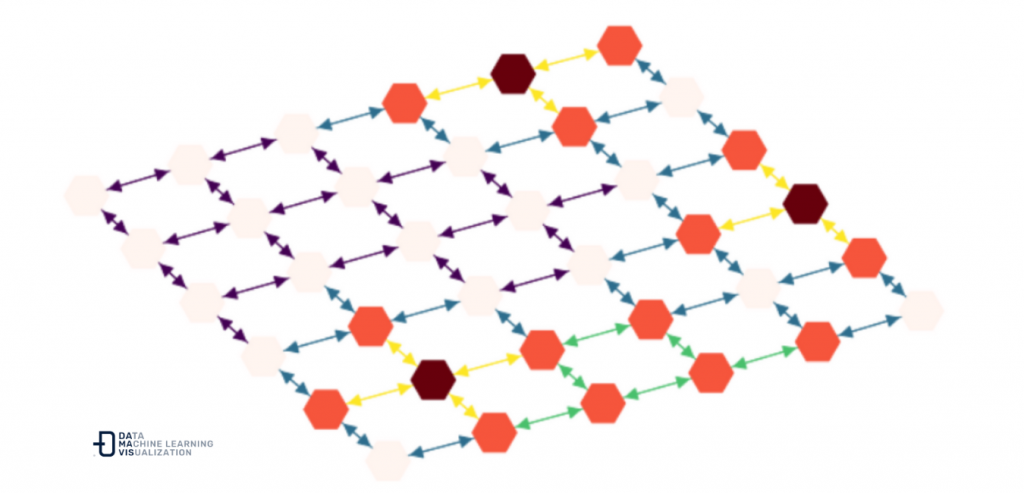
Now we are going to deal with the edges (corridors) that connect our nodes (rooms). These corridors will have an average temperature obtained between the temperature of the rooms they connect.
So, if we traverse each edge of the graph we can calculate the temperature and assign it as follows:
for edge_ori, edge_dest in list(DG.edges()):
DG.add_edges_from(
[(edge_ori, edge_dest)],
edge_temp=np.mean(
[DG.nodes[edge_ori]["node_temp"],
DG.nodes[edge_dest]["node_temp"]]
)
)
Therefore, if what we want is to find the optimal route from the starting point (in this case, the right end node) to the end point (the left end node), we can use one of the algorithms that solve this type of problem in a computationally optimal way.
Algorithm A*, which works as shown in the following image:

Thus, if we use this system without taking into account the temperatures of the nodes, we would find one (there may be several) of the shortest routes from the starting point to the end point as the answer.
nx.astar_path(DG, start_node, end_node)
[(0, 0),
(1, 0),
(2, 0),
(3, 0),
(4, 0),
(5, 0),
(5, 1),
(5, 2),
(5, 3),
(5, 4),
(5, 5)]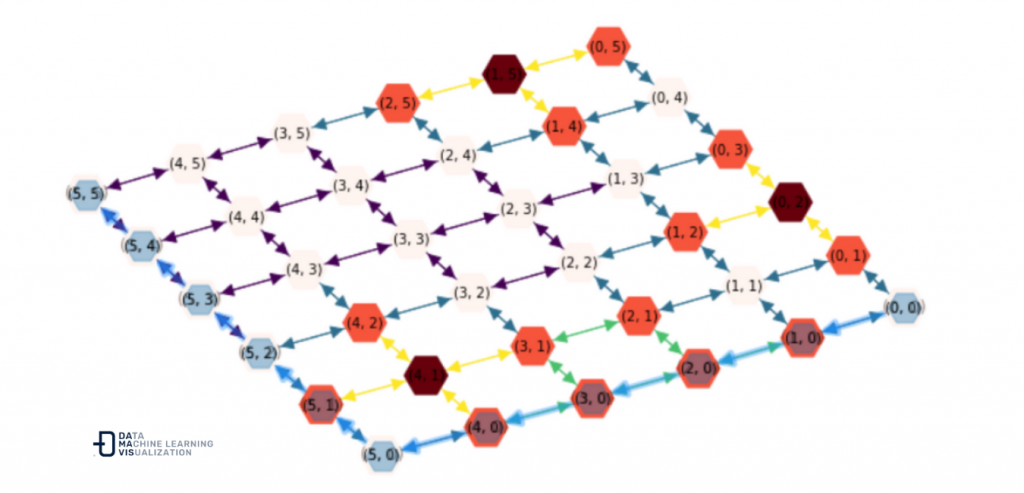
But as we said, this is not what we are looking for, because if we were to go through all the rooms indicated by the shortest route, we would cross rooms and corridors with very high temperatures.
So let’s repeat the process, this time taking into account the temperatures to find the shortest and coldest route possible.
nx.astar_path(DG, start_node, end_node, weight='edge_temp')
[(0, 0),
(1, 0),
(1, 1),
(2, 1),
(2, 2),
(3, 2),
(3, 3),
(4, 3),
(5, 3),
(5, 4),
(5, 5)]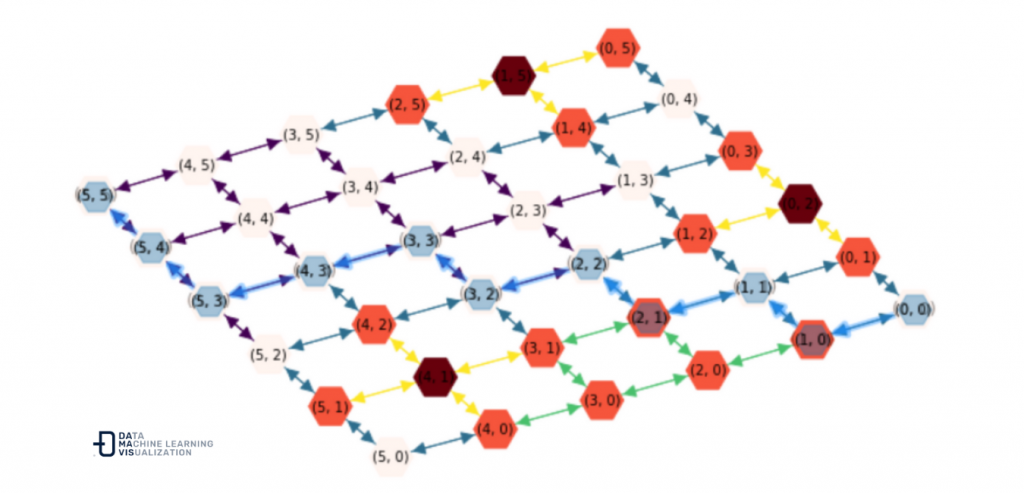
In this way we already have a system that solves the problem we have stated in a matter of milliseconds.
However, what would happen if, in addition, we remove some nodes from our network, simulating rooms inaccessible by fire? for example:
to_remove = [
(5, 1), (4, 2), (3, 3),
(0, 2), (1, 1), (2, 1)
]
for node in to_remove:
DG.remove_node(node)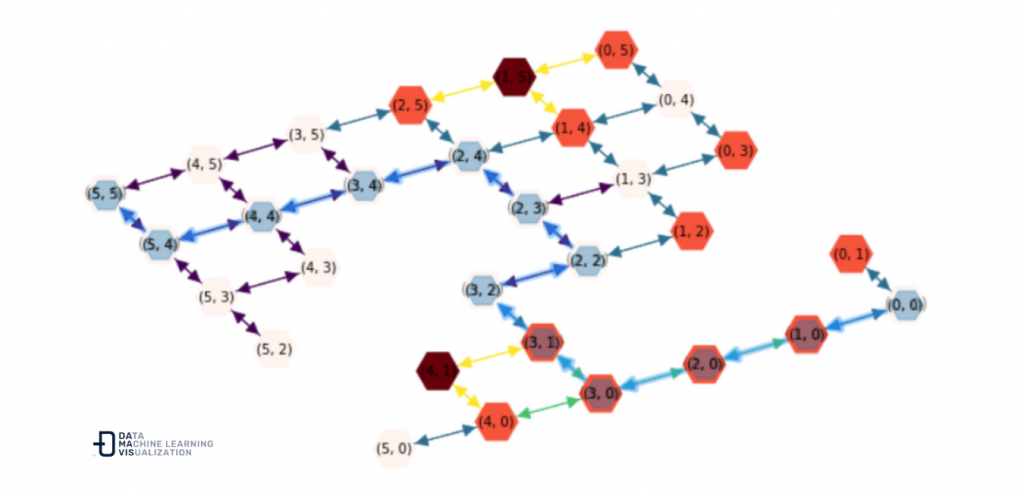
The route is adapted to the environment and again we obtain the most optimal route taking into account the temperature of the route.
In this way, with the algorithm already prepared, we can generate a much larger environment and make the algorithm face a larger number of decisions to make in order to find the optimal route.
For example, by generating a new graph with 2500 nodes and 150 hot spots to be taken into account.

And with the same ease of the already programmed, we obtain the optimal route to the exit.
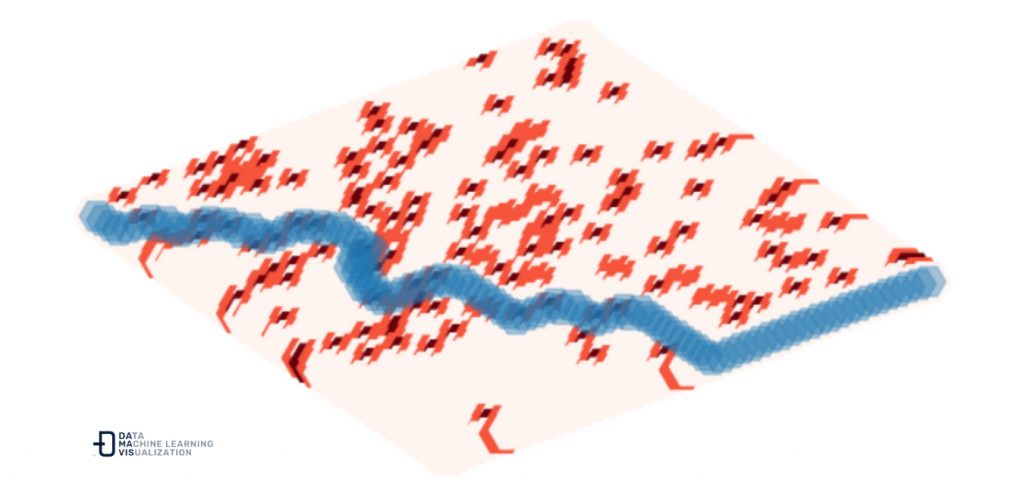
Obviously this is a simple example of the use of graphs to explain how they can be used to solve certain problems. These same tools can be useful to solve different problems that we can find in companies on a daily basis.
Here are some examples of different complexities that can be worked on with a graph system and choice of optimal routes:
- Optimisation of warehouse space
- Distribution of goods
- Fuel savings in vehicle fleets
- Optimisation of product purchase / sale rules
The code of the exposed example is at https://github.com/ so you can download it and use it yourself.

