Colony of ants to find the shortest route

In our blog article Graphs – Finding optimal routes we introduced the use of graphs to find optimal routes. This time, we will study a technique to solve this problem that is inspired by the behavior of ant colonies. In case you are not very fluent in the subject, it is recommended that you first review the article mentioned above.

Collective Intelligence

In the context of computer science, heuristics are techniques to approximate solutions to a problem, normally used when there is no direct method to reach the solution or when the existing ones are too slow. When faced with a problem, a heuristic will offer us a possible solution, but it cannot guarantee that it is really the optimal one. When a heuristic is broad enough to be applied in a generalized way to multiple problems, it is a metaheuristic.

Among the various metaheuristics that exist, ant colony optimization belongs to the swarm or collective intelligence type, which includes techniques that in one way or another mimic the functioning of social communities in animal nature. In these systems, starting from a set of unintelligent individuals, a remarkable intelligence derived from the interaction among them can emerge.

Ants searching for resources

In nature, ants look for resources, mainly food, that are outside their nest, so they have to travel to them and back. The shorter that path, the less time the ant spends exposed to danger from outside and the sooner it will obtain them.

As the different foraging ants follow a common goal, they collaborate with each other by leaving a pheromone trail, with which they can communicate with each other. Each time an ant encounters an obstacle, it must choose a possible path, this decision being probabilistic and influenced by the amount of pheromone deposited at that moment. A greater amount of pheromone on a path will favor its choice, but it will not determine it.

If in front of an obstacle there are several paths and one of them is shorter, the ants that take that path will arrive and return before the resource, and in this way, when the next ant arrives, there will be a little more pheromone on that path, so it will be more likely to take it and the discovery will be propagated. On the other hand, pheromone evaporates over time, so if a path is no longer traveled, the pheromone will be lost and therefore the extra stimulus for new ants to take it.

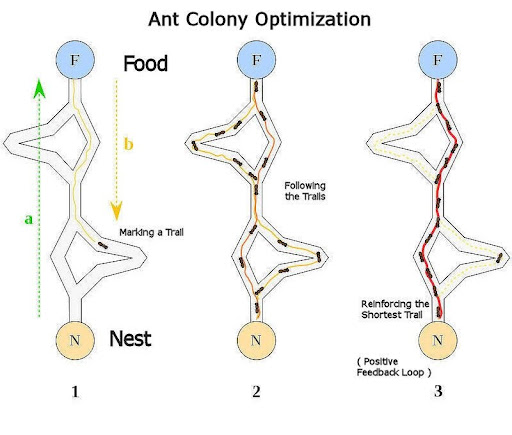
Artificial ants

Bringing these dynamics to the world of algorithms, the system would have m “artificial ants”, each of them being a mechanism for constructing solutions, in this case paths. Likewise, if we represent the problem to be solved as a graph G(V, E), we have that the weight c_ij of each edge (_i,j) ∈ E is equivalent to the distance between the vertices it joins, and to take into account the pheromone, each edge will have an associated numerical value τ_ij , which will represent the amount of pheromone deposited.

Normally, all pheromones are usually initialized with the same value, in this case τ₀ = m/Cⁿⁿ , where Cⁿⁿ is the cost of the solution found by a voracious heuristic. The information of the weight c_ij of an edge is valuable when making a decision, so we can define the heuristic values η_ij = 1/c_ij . To avoid repeating nodes, each ant will maintain a list of vertices already visited. N_k(i) will be the set of nodes neighboring vertex i that have not been visited by ant k.

With all the factors stated above, we can go on to state the transition rule, that is, the probability p_ij^k that ant k, located at vertex i takes the path to vertex j:

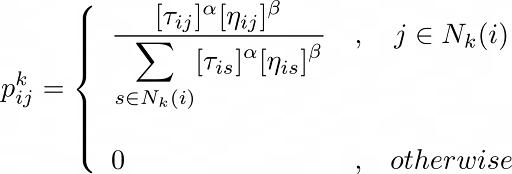
α and β are positive parameters representing the influence of the pheromone and weight heuristics respectively. If α is high, the more pheromone tracts will be preferred, and if β is high, the expensive tracts will be preferred. The key is to find a balance between the two.

Once we know how the ants act, it remains to understand how the pheromone update takes place, which will be the result of evaporation and the contribution of new pheromone, as follows:

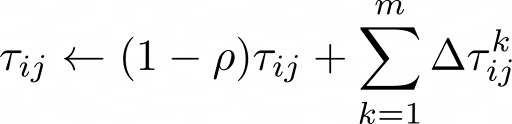
ρ ∈ (0, 1] is the evaporation factor, which will determine at what rate the deposited pheromone evaporates. ∆τ_ij^k represents the pheromone deposited on edge (i,j) by ant k, which will be larger the shorter the generated circuit.

The stopping conditions used for the algorithm are either a preset number of iterations or that a stagnation state is reached.

To see how the algorithm works in a global way, let’s see a pseudocode of the algorithm:

initialize
while not stopping criteria:
 for every ant:
	while path not done:
		calculate transition probabilities pijk
		apply decision policy to move to the next vertex
 update pheromones
 update best solution
return best solution

Conclusion

We have studied the theoretical framework of the simplest version of this technique; however, since its first appearance, new and more sophisticated versions have arrived, such as those that incorporate ideas of genetic algorithms or elitism in the contribution. If there is one thing we can learn from techniques such as ant colony optimization, it is that the intelligent phenomena observed in nature are the best source of inspiration for developing new artificial intelligence systems.

To further explore this subject, we recommend the work of the promoter of this technique, Marco Dorigo, which has served as a reference for this entry. In addition to his doctoral thesis on the subject, we recommend the following article.

If you found this article interesting, we encourage you to visit the Algorithms category of our blog to see posts similar to this one and to share it in networks with all your contacts. Don’t forget to mention us so we can know your opinion @Damavisstudio. See you soon!