En el artículo de nuestro blog Grafos – Encontrando caminos óptimos se introdujo el uso de grafos para encontrar rutas óptimas. Ahora, estudiaremos una técnica para resolver dicho problema que se inspira en el comportamiento de las colonias de hormigas. En caso de que no cuente con mucha soltura en la materia, se recomienda revisar primero el artículo anteriormente mencionado.
Inteligencia Colectiva
Dentro del contexto de las ciencias de la computación, las heurísticas son técnicas para aproximar soluciones de un problema, normalmente usadas cuando no existe método directo de alcanzar la solución o cuando los existentes son demasiado lentos. Ante un problema, una heurística nos ofrecerá una posible solución, pero no podrá garantizarnos que sea realmente la óptima. Cuando una heurística es lo suficientemente amplia como para poder ser aplicada de forma generalizada en múltiples problemas, se trata de una metaheurística.
De entre las diversas metaheurísticas que existen, la optimización por colonia de hormigas pertenece al tipo Inteligencia de enjambre o colectiva, donde se encuentran las técnicas que de una forma u otra imitan el funcionamiento de comunidades sociales en la naturaleza animal. En estos sistemas, partiendo de un conjunto de individuos poco inteligentes puede emerger una inteligencia notable derivada de la interacción entre los mismos.
Hormigas buscando recursos
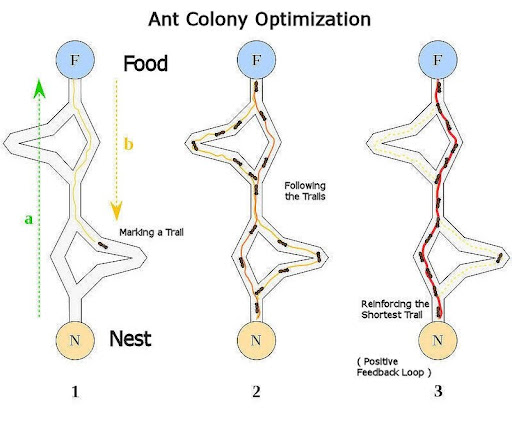
En la naturaleza, las hormigas buscan recursos, principalmente comida, que se encuentran fuera de su hormiguero, por lo que tienen que desplazarse hasta ellos y volver. Cuanto más corto sea ese camino, menos tiempo pasará la hormiga expuesta al peligro del exterior y antes los obtendrá.
Como las diferentes hormigas recolectoras siguen un objetivo común, colaboran entre sí dejando un rastro de feromona, con el que pueden comunicarse entre ellas. Cada vez que una hormiga encuentra un obstáculo, deberá elegir un posible camino, siendo esta decisión probabilística e influenciada por la cantidad de feromona que se encuentre depositada en dicho momento. Una mayor cantidad de feromona en un camino favorecerá su elección, sin embargo, no la determinará.
Si ante un obstáculo hay varios caminos y alguno de ellos es más corto, las hormigas que tomen ese camino llegarán y volverán antes del recurso, y de esta forma, cuando llegue una hormiga siguiente, habrá un poco más de feromona en dicho camino, por lo que tendrá mayor probabilidad de tomarlo y se propagará el descubrimiento. Por otro lado, la feromona se evapora con el paso del tiempo, por lo que si un camino deja de ser transitado, se perderá la feromona y por tanto el estímulo extra a que nuevas hormigas lo tomen.
Hormigas artificiales
Trayendo estas dinámicas al mundo de los algoritmos, el sistema contaría con m “hormigas artificiales”, siendo cada una de ellas un mecanismo de construcción de soluciones, en este caso de caminos. Asimismo, si representamos el problema a resolver en forma de grafo G(V, E), tenemos que el peso cij de cada arista (i,j) ∈ E equivale a la distancia entre los vértices que une, y para tener en cuenta la feromona, cada arista tendrá asociado un valor numérico τij, que representará la cantidad de feromona depositada.
Normalmente, todas las feromonas suelen inicializarse con el mismo valor, en este caso τ0 = m/Cnn, donde Cnn es el coste de la solución encontrada por un heurístico voraz. La información del peso cij de una arista resulta valioso a la hora de tomar una decisión, por lo que podemos definir los valores heurísticos ηij = 1/cij . Para evitar repetir nodos, cada hormiga mantendrá una lista de vértices ya visitados. Nk(i) será el conjunto de nodos vecinos al vértice i que no han sido visitados por la hormiga k.
Con todos los factores enunciados anteriormente, podemos pasar a enunciar la regla de transición, es decir, la probabilidad pijk de que la hormiga k, situada en el vértice i tome el camino hacia el vértice j:
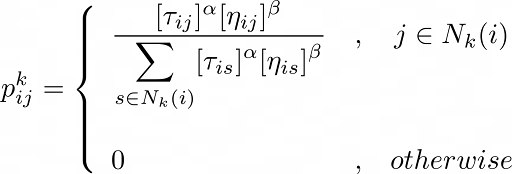
α y β son parámetros positivos que representan la influencia de la feromona y la heurística del peso respectivamente. Si α es alto, se tendrá preferencia por los tramos con más feromona, y si β es alto, se preferirán los tramos costosos. La clave está en encontrar un equilibrio entre ambos.
Una vez que sabemos cómo se desarrolla la actuación de las hormigas, queda entender cómo se produce la actualización de feromona, que será el resultado la evaporación y el aporte de nueva feromona, de la forma:
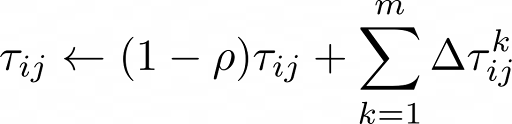
ρ ∈ (0, 1] es el factor de evaporación, que determinará a qué ritmo se evapora la feromona depositada. ∆τijk representa la feromona depositada en la arista (i,j) por la hormiga k, que será mayor cuanto más corto sea el circuito generado.
Las condiciones de parada empleadas para el algoritmo son bien un número prefijado de iteraciones o que se alcance un estado de estancamiento.
Para ver de forma global el funcionamiento del algoritmo, veamos un pseudocódigo del mismo:
initialize
while not stopping criteria:
for every ant:
while path not done:
calculate transition probabilities pijk
apply decision policy to move to the next vertex
update pheromones
update best solution
return best solutionConclusión
Hemos estudiado el marco teórico de la versión más sencilla de esta técnica, sin embargo, desde su primera aparición han llegado nuevas versiones más sofisticadas, como las que incorporan ideas de algoritmos genéticos o elitismo en la contribución. Si algo podemos extraer de técnicas como la optimización por colonia de hormigas, es que los fenómenos con inteligencia que se observan en la naturaleza son la mejor fuente de inspiración de cara a desarrollar nuevos sistemas de inteligencia artificial.
Para seguir profundizando en esta materia, se recomienda la obra del promotor de esta técnica, Marco Dorigo, que ha servido como referencia para realizar esta entrada. Además de su tesis doctoral al respecto, se recomienda el siguiente artículo.
