En el mundo del análisis y la ciencia de datos, las series temporales son una pieza clave, pues representan una fuente de información muy natural: valores de una magnitud en distintos instantes temporales. Es por esto que entender sus propiedades y saber trabajar con ellas es necesario para desarrollar satisfactoriamente proyectos en estos campos.
En este post, vamos a mover nuestro foco de interés en las propiedades de las series temporales que surgen de compararlas y relacionarlas con otras.
Con muy alta probabilidad, lo primero que se nos viene a la cabeza al hablar de relacionar distintas series temporales es evaluar en qué medida “son iguales” o al menos “tienen la misma tendencia”. Por supuesto, esta medida es muy relevante y existen gran cantidad de métricas para medir esto, algunas tan fundamentales y reconocidas como la correlación en su definición más básica.
Pero supongamos por un momento que dos series temporales son exactamente iguales, pero una la retrasamos respecto de la otra un número cualquiera de unidades temporales. Si evaluáramos visualmente la situación, diríamos que son la misma serie temporal “solo que desplazadas”, pero, sin embargo, los algoritmos mencionados no devolverán un valor que indique eso con tanta claridad.
Entender cuando ocurre esto es muy importante, puesto que además puede llegar a responder a preguntas sobre la relación entre series temporales de grandísima relevancia: ¿Tiene una cierta variable poder predictivo sobre otra? O incluso, ¿una cierta variable afecta el comportamiento de otra? Para descubrirlo a nivel matemático, por supuesto, hay que introducir un algoritmo que sea capaz de conseguirlo. Uno de los más conocidos es la “causalidad de Granger”, y en este post vamos a introducir y explicar este método.
Un poco de historia
El método de la causalidad de Granger fue introducido en 1969 por el economista, y ganador del premio Nobel de literatura en 2003, Sir Clive William John Granger, en su afamado artículo titulado: Investigación de relaciones causales a través de modelos econométricos y métodos espectrales cruzados.
El área de aplicación inicial de esta metodología fue la economía. Sin embargo, tras más de 50 años desde su introducción, los campos del conocimiento en los que se ha usado solo han hecho que aumentar. Hasta el punto que a día de hoy aplicaciones de este algoritmo se pueden encontrar en ramas muy dispares, desde la neurociencia hasta el transporte aéreo, pasando por la climatología y la meteorología.
El hecho de que después de tanto tiempo esta metodología se siga empleando y que cada vez lo haga con más interdisciplinariedad, es una prueba más de su correcto funcionamiento y aplicabilidad.
Idea cualitativa
La idea cualitativa detrás de este algoritmo es que una serie temporal Y “causa” otra serie temporal X, si conociendo adicionalmente valores pasados de Y (respecto a valores de X que vamos a tratar de predecir) mejora la predicción de valores de X, respecto a solo usar valores pasados de X.
Es muy importante entender por qué hemos utilizado comillas cuando hemos escrito la palabra causa: el término causar, si lo usáramos en sentido literal, en este contexto implicaría que si la mencionada causalidad existe, hay algo en la magnitud que representa Y que está afectando directamente a la que representa X, que hace que conociendo valores pasados de Y se pueda entender mejor cómo evoluciona X.
Al ser un algoritmo matemático, esta relación causa-efecto no se asegura bajo ninguna circunstancia, aunque este concluya existencia de causalidad. Poniendo un ejemplo muy trivial, de manera independiente, dos altavoces se pueden configurar para que emitan la misma señal, uno de los dos con un segundo de retraso; y mientras que no existe relación causa-efecto entre los dos, este algoritmo sí detectará la causalidad.
El motivo por el que se emplea el término causalidad es por ser consistente con la nomenclatura propuesta por su autor, y por compacidad en la notación; pero muy probablemente el término “capacidad de predicción” en este contexto sea mucho más adecuado. De esta manera, cuando digamos Y causa X, estaremos en realidad diciendo que Y tiene capacidad de predicción sobre X.
Desarrollo matemático
Habiendo entendido la idea cualitativa detrás del algoritmo, es momento de introducir el marco matemático de esta metodología que nos va a permitir implementarlo con series temporales reales.
Antes de comenzar, es necesario mencionar que la metodología que se va a presentar en este post es la originalmente introducida por C. W. J. Granger en su artículo original; pero no es el único desarrollo existente.
Analizando la idea cualitativa presentada en el párrafo anterior, para poder aplicarla, tenemos que ser capaces de evaluar matemáticamente cómo de bien se predicen los valores de X utilizando tanto valores pasados de X y como de Y; como solo valores pasados de X. Para ello, vamos a generar dos modelos de regresión.
Primero, cuando usamos las dos series temporales:
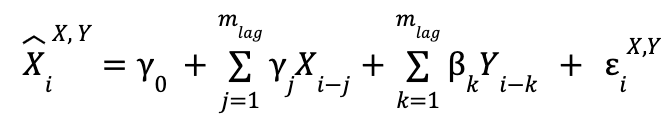
y cuando solo usamos los datos pasados de X:
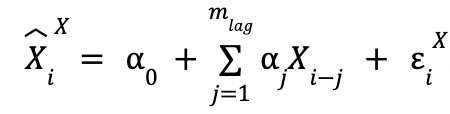
es el valor que predecimos para elemento i-ésimo de la serie temporal X, y el superíndice indica de qué series temporales son los valores pasados que estamos usando (en la variable utilizada para la explicación, , serían de X e Y).
es el valor en el paso temporal 
de la serie temporal X. 
es el error cometido en la predicción de, para este caso, el valor 
, donde el significado del superíndice y del subíndice son los mismos en estas dos variables. Los sumatorios van hasta 
, que es el número de valores pasados que se van a tomar para realizar las predicciones (o dicho de otra manera, el número de unidades temporales que el valor más pasado utilizado en las predicciones va a tener respecto del que se busca predecir). El valor de este parámetro no viene fijado de antemano y es modificable.
Finalmente, los α, β y γ son los parámetros a ajustar, por lo que tampoco tienen un valor prefijado. Para poder distinguir ambos modelos, y teniendo en cuenta que el que solo utiliza datos de la serie temporal X es un caso específico del que utiliza ambas (tomando en el primero todas las β como 0 se regresa al primero), vamos a llamar al primero “modelo restringido” y al segundo “modelo no restringido”.
Hemos comentado que hay ciertos parámetros cuyo valor tiene que ser encontrado. Según la teoría original presentada por Granger, las predicciones más óptimas de cada uno de los modelos son aquellas que minimizan la varianza de los errores cometidos en las predicciones, respectivamente. Matemáticamente, esta varianza toma la expresión:
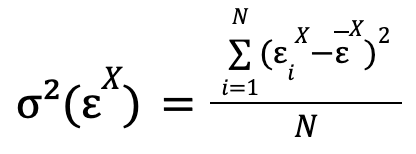
donde el sumatorio recorre los errores de todas las predicciones que se han realizado con el modelo del que se desea calcular la varianza del error de valores de la serie temporal X (modelo restringido en el caso del ejemplo puesto), y que en la fórmula se ha asumido que han sido N. 
es la media de los errores.
Por lo general, esta última media siempre va a poder tomar el valor de 0 (y, aunque en este punto el que lo tome no es necesario, veremos que para una evaluación necesaria de este modelo, sí lo es), pues en caso de que no tome ese valor, lo que está indicando es que existe un sesgo constante en el modelo (en promedio, todas las predicciones son erróneas por un determinado valor), algo que se soluciona sumando ese mismo valor al término independiente del modelo.
Bajo esta casuística, minimizar la varianza es equivalente a minimizar la suma de los cuadrados de los errores y, por ello, el error cometido en las predicciones. Los sets de parámetros α, β y γ son los que se ajustan, respectivamente para cada modelo, para conseguir la mencionada minimización. Todavía queda un último parámetro por fijar, que sería , pero por el momento no vamos a mencionar cómo se determina su valor, y simplemente asumiremos que toma un valor cualquiera, eso sí, mayor o igual que 1.
Siguiendo con la explicación de C. W. J. Granger, diremos que la serie temporal Y causa la serie temporal X si:
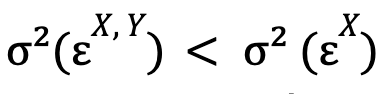
es decir, si la varianza del error optimizada para el modelo no restringido es menor que esta misma magnitud para el modelo restringido. Si adicionalmente también se verifica:
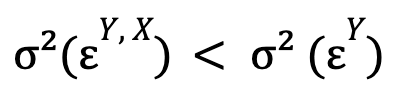
(es decir, la serie temporal X causa la serie temporal Y), diremos que existe retroalimentación (término original: feedback) entre estas dos series temporales.
Antes de concluir esta sección, es muy importante mencionar una serie de restricciones que tiene este algoritmo. La primera de ellas es que, para poder trabajar con esta metodología es necesario que ambas series temporales con las que se estén trabajando sean estacionarias.
Puesto que no es el objetivo de este post, la explicación formal de cuando una serie temporal es estacionaria y cómo poder comprobarlo no se va a explicar, pero sí se va a hacer mención a una idea cualitativa de la misma y el motivo por el que es necesario en esta metodología. Una serie temporal es estacionaria si sus propiedades (como por ejemplo su varianza) no son función del tiempo; es decir, cuando se van haciendo los cálculos para distintos intervalos de la serie temporal, los valores obtenidos para las magnitudes representativas son las mismas. El motivo por el que necesitamos que lo sean para poder aplicar la causalidad de Granger, es que, si no lo fueran, propiedades como por ejemplo la varianza del error que usamos para poder obtener una conclusión, no se puede asegurar que no vayan a variar en el tiempo y, por ello, no se podría concluir nada.
La segunda restricción es que para maximizar la fiabilidad del algoritmo, las series temporales no pueden tener falta de datos, es decir, tienen que tener un valor asignado para cada paso temporal.
Interpretación estadística
Si uno comienza a poner en práctica lo explicado en el párrafo anterior, haciendo pruebas con distintos pares de series temporales estacionarias, rápido se daría cuenta de que, muy sospechosamente, en prácticamente todos los casos, la mencionada causalidad (y más específicamente retroalimentación) entre los pares de series temporales ocurre.
Por supuesto, no es que todas estas causalidades estén sucediendo realmente. Lo que en realidad pasa es que, tal y como vamos a ver ahora, en la evaluación planteada en el párrafo anterior, los propios modelos propuestos, por construcción, están prácticamente asegurando que la condición de causalidad se satisfaga siempre. Como ya mencionamos en la pasada sección, el modelo de regresión cuando solo usamos una serie temporal es un caso específico del modelo de regresión no restringido. De esta manera, el modelo no restringido siempre va a tener una menor varianza del error o, en el peor de los casos, igual si la minimización de esta magnitud en el primero se alcanza cuando 
(en cuyo caso ambos modelos optimizados serían el mismo, i.e. 
), de manera que por construcción siempre vamos a tener (para el caso donde estudiamos si Y causa X):
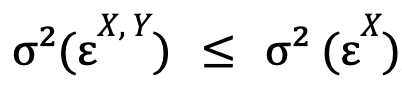
donde, además, la igualdad es un caso extremo altamente improbable.
Para solucionar este problema, el cambio cualitativo que tenemos que dar a la hora de la evaluación de los resultados es pasar de responder la pregunta: ¿Puedo predecir mejor valores de X utilizando también valores pasados de Y? Que ya sabemos que la respuesta va a ser siempre sí (o como mínimo igual de bien), a responder a la pregunta: ¿Mi predicción utilizando también valores de Y mejora lo suficiente respecto a la que solo usamos los de X, considerando que en esta última doblamos tanto los parámetros a ajustar como los valores que se usan?
Para poder responder a esta última pregunta tenemos que movernos a un contexto más estadístico. La idea intuitiva es que si el poder de predicción de la segunda serie temporal sobre la primera es bajo, todos los coeficientes estarán muy cercanos a cero, donde esa cercanía se valorará en función de las facilidades que tenga el modelo no restringido en conseguir mejores predicciones que el restringido. Es por ello que el test estadístico que vamos a proponer toma como hipótesis nula: Todos los coeficientes β del modelo no restringido son 0, y por tanto la hipótesis alternativa es: Al menos un coeficiente β del modelo no restringido es distinto de 0. Para determinar qué hipótesis es la verdadera (en sentido estadístico), se va a calcular el próximo valor (denominado F-score):
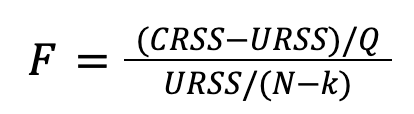
donde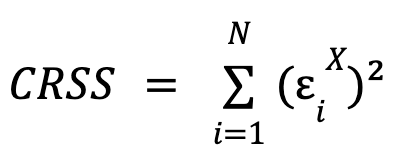 
y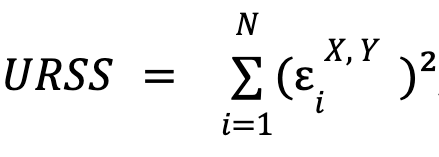 
, es decir, la suma de los cuadrados de los errores para cada modelo. 
es el número de restricciones impuestas en el modelo restringido (igual al número de parámetros β), 
el número de valores de la serie temporal X para los que se han hecho predicciones y 
el número total de parámetros a ajustar en el modelo no restringido (igual a la suma del número de parámetros β y γ).
Considerando que la media del error se puede fijar siempre en 0, 
y 
son proporcionales a las respectivas varianzas de los errores. De manera intuitiva se puede ver que esta magnitud 
es la distancia entre las dos varianzas (además siempre será positiva, puesto que por construcción 
), normalizada por “la facilidad” que tiene el modelo no restringido en hacer predicciones más óptimas que el restringido. Esto último lo vemos en el hecho de que va dividiendo, lo que nos indica que cuanto menos parámetros libres tenga el modelo restringido con respecto al no restringido, más fácil va a ser que por construcción el segundo haga mejores predicciones que el primero; y por tanto, con el resto de valores fijos esta “distancia” entre ambos se reduce a medida que aumenta. 
va multiplicando puesto que cuanto mayor sea esta diferencia (o equivalentemente, mayor sea el valor de ), la diferencia en el número de parámetros a ajustar de cada modelo será menos notoria y, por tanto, estarán en más igualdad de condiciones en términos de poder hacer predicciones precisas. El término dividiendo se puede entender como un factor de normalización para que la magnitud sea adimensional.
La manera formal de pensar este test estadístico es que la diferencia entre y (normalizada por el resto de factores) sigue una distribución de 
si la hipótesis nula es cierta.
Para evaluar las hipótesis, se transforma el valor de en un p-valor (gracias a que tal y como hemos mencionado, esta diferencia sigue una determinada distribución en caso de que la hipótesis nula sea cierta). Si el valor de está por encima de un cierto umbral (equivalente al p-valor por debajo de otro cierto umbral que se suele tomar como 0.01), la diferencia entre y es lo suficientemente grande como para considerar que el modelo no restringido hace mejor predicciones que el restringido, rechazándose así la hipótesis nula, y considerándose que existe causalidad (i.e. el resultado 
es estadísticamente significativo). Mientras que si el resultado es el opuesto, la hipótesis nula se acepta y no existe dicha causalidad.
Volviendo al parámetro que nos dejamos por fijar, , la primera restricción que tiene este suele venir impuesta por el significado físico de las series temporales, o por estar interesados en estudiar un cierto lag en específico. En caso de que tras esto la comprobación se quiera realizar con un conjunto de lags, el que genera la causalidad más significativa, en caso de que haya un conjunto de ellos que satisfagan la condición de causalidad, es aquel que minimice el p-valor o equivalentemente maximice .
Finalmente, es muy importante tener en cuenta que para poder aplicar esta metodología necesitamos que los errores asociados a las predicciones, para cada uno de los modelos, cumplan el requisito de seguir una distribución normal, centrada en el 0 (aquí la razón por la que mencionamos que ya no solo es que pudiéramos llevar la media a los errores a 0, si no que lo íbamos a necesitar). En notación matemática: 
.
Ventajas y restricciones de la causalidad de Granger
La causalidad de Granger tiene una serie de desventajas cuando se quiere utilizar para encontrar causalidades entre series temporales, que es necesario mencionar:
- Al ser una metodología puramente matemática, no permite una explicación de esa causalidad, pues una que ocurra como consecuencia de causa-efecto es indistinguible, para este algoritmo, de una que pase por casualidad.
- No es capaz de distinguir cuando el comportamiento de dos series temporales viene determinado por una tercera serie temporal distinta, de cuando viene determinado entre ellas.
Sin embargo, es necesario tener en cuenta que estos problemas y limitaciones se encuentran en todos los algoritmos de causalidad que trabajan con solo dos series temporales a la vez. Los que trabajan con más series temporales a la vez, es muy probable que la desventaja 2 no lo tengan, pero el coste computacional de estos algoritmos aumenta enormemente.
Pese a esto, funciona mejor que otros métodos de su misma clase, como la regresión con lag, en la que no se evalúa el poder predictivo de la segunda serie temporal en el contexto de poder usar también valores de la primera.
Conclusión
En este artículo, hemos analizado las propiedades de las series temporales que aparecen al relacionarlas y compararlas entre sí. Gracias a ellas, podemos obtener nueva información relevante de los datos que, de evaluar individualmente las series temporales, se encontraría “oculta”.
