En los últimos años cada vez más empresas utilizan el aprendizaje automático y la estadística para optimizar sus procesos de negocio. El análisis de supervivencia es una rama de la estadística poco conocida pero que puede resultar de utilidad en muchas situaciones. En este post mostramos algunos conceptos básicos de análisis de supervivencia y veremos cómo puede usarse en un caso de negocio real.
Conceptos básicos
El análisis de supervivencia estudia el tiempo hasta la ocurrencia de un suceso. Este tiempo se denomina tiempo del evento y es una variable aleatoria no negativa que nos indica el tiempo entre dos eventos de interés. Por ejemplo, desde la aplicación de un tratamiento hasta la muerte del sujeto o desde la instalación de una maquinaria hasta que ésta falla. Se suele denotar con 𝛵.
Si consideramos la probabilidad de que el tiempo del evento sea mayor que un cierto valor, obtenemos lo que se conoce como curva de supervivencia. Matemáticamente se representa como 𝑆(𝑡) y se define como 𝑆(t) = 𝑃(𝛵>𝑡) =1-𝑃(𝛵𝑡) = 1 – 𝐹(𝑡) donde 𝐹(𝑡) es la función de probabilidad acumulada.
La función de riesgo en un tiempo t representa la probabilidad de que suceda el evento de interés en el instante inmediatamente posterior a 𝑡. Matemáticamente se representa como ℎ(𝑡) y viene definida por ℎ(𝑡) = 𝑓(𝑡) / 𝑆(𝑡) donde 𝑓(𝑡) representa la función de probabilidad de la variable aleatoria 𝛵.
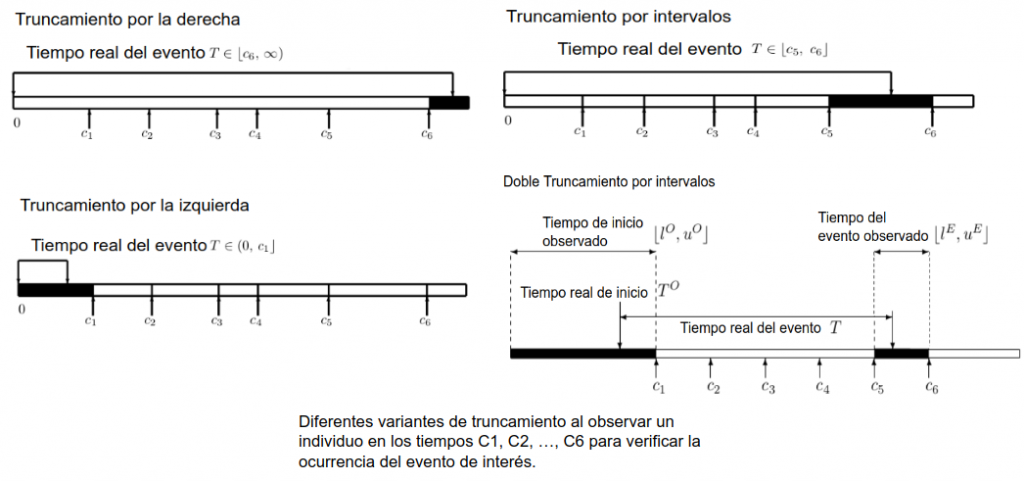
Una de las características más comunes en los datos de estudios de análisis de supervivencia es el truncamiento o censoring. Este se produce cuando no conocemos el tiempo exacto en el que ocurre el evento de interés.
Entendemos que existe truncamiento por la derecha cuando sabemos que el evento ocurre después de un momento 𝑡1 pero no exactamente cuando. Este tipo de truncamiento es común en los estudios médicos, en los que se sigue a los participantes por una cantidad determinada de tiempo y el evento no ocurre para algunos de ellos antes de que acabe el estudio.
El truncamiento por la izquierda ocurre cuando se conoce que el evento ocurre antes de un momento 𝑡1 pero no conocemos exactamente cuando.
Un último tipo de truncamiento es el truncamiento por intervalos. Este se produce cuando no sabemos el momento exacto de uno de los eventos de interés pero sabemos que éste sucede entre dos instantes 𝑡1 y 𝑡2. Un tipo especial de truncamiento por intervalos es el doble truncamiento por intervalos, que se manifiesta cuando disponemos de un intervalo para cada uno de los eventos de interés.
La siguiente figura muestra gráficamente cada uno de los tipos de truncamiento.
¿Por qué no regresión lineal o logística?
La presencia de observaciones con algún tipo de truncamiento es lo que imposibilita en muchos casos el uso de métodos tradicionales de regresión. Sin embargo, incluso con la ausencia de truncamiento el análisis de supervivencia es preferible debido a otras dos razones:
- El tiempo del evento es una variable aleatoria que tiene sesgo además de estar restringida a los reales positivos lo cual no encaja con las distribuciones usadas en los modelos de regresión lineal.
- En muchos casos el objetivo no es entender el tiempo promedio al evento sino la forma de la curva de supervivencia o la función de riesgo.
Cambios de precio de boletos de avión
En los portales de venta de vuelos como Skyscanner, Kayak, o Edreams, los usuarios suelen consultar un vuelo en diversas ocasiones antes de decidirse a comprarlo. En cada una de estas consultas el portal debe hacer una petición al proveedor lo cual puede incrementar el coste operativo así como saturar el servidor del proveedor.
En respuesta a este problema, muchos portales crean una base de datos con los vuelos y precios que les han consultado recientemente y solo piden al proveedor cuando el usuario ya está a punto de comprar. A esta base de datos se le llama comúnmente memoria caché.
El tener una memoria caché tiene sus propios obstáculos ya que almacenar datos también tiene un coste para la empresa. Lo ideal es almacenar sólo aquellos vuelos que van a volver a consultar en el futuro y hacerlo durante el mayor tiempo posible siempre y cuando el precio del boleto mostrado no haya cambiado.
La segunda problemática es la que nos atañe en este post. Es decir, dado un conjunto de boletos almacenados en caché ¿cual es el tiempo que debo mantenerlos en la memoria de forma que se minimicen los costes así como la diferencia entre el precio mostrado y el precio final al que compra el cliente?
Esta pregunta sigue siendo compleja, ya que se deben tener en cuenta costes que son variables en el tiempo como los costes monetarios incurridos en almacenamiento y el coste subjetivo de proporcionar un precio erróneo al usuario. No obstante, podemos simplificar la pregunta a una cuya respuesta proporcione información útil sin importar cuales sean los costes.
Nos planteamos entonces ¿cuál es la probabilidad de que el precio de un boleto siga estando vigente dado el número de días que lo hemos tenido almacenado en la memoria?
Respondiendo esta pregunta podemos dotar a la empresa de información que se puede usar para establecer posteriormente umbrales subjetivos. Por ejemplo, que solo se mantenga un precio en la caché si y sólo si la probabilidad de que este siga vigente es mayor al 80%.
Para usar el análisis de supervivencia en este caso, asumimos que el cambio de precio es el evento de interés y cada precio/boleto es un individuo que nace, vive por un tiempo y muere. Dado que estos portales disponen de múltiples proveedores y tipos de vuelo se opta por un modelo paramétrico de forma que se estimen indirectamente diferentes curvas de supervivencia.
En concreto, se usará el AFT con distribución de Weibull, el cual modela el logaritmo del tiempo del evento y origina una curva de supervivencia que viene dada por una función sencilla:
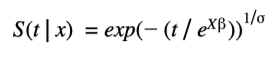
Donde 𝑘 y λ son los parámetros de forma y escala de una distribución de Weibull y 𝛽 es el vector con la influencia de las variables explicativas χ.
Debido al volumen de datos manejado por estos portales de vuelos, PySpark puede ser en muchos casos la única opción para el entrenamiento del modelo usando todos los datos (consulta la documentación de Apache Spark )
Los datos proporcionados por la empresa son peticiones realizadas a los proveedores que nos muestran las características del vuelo, la fecha en que se hizo la petición y el precio obtenido:
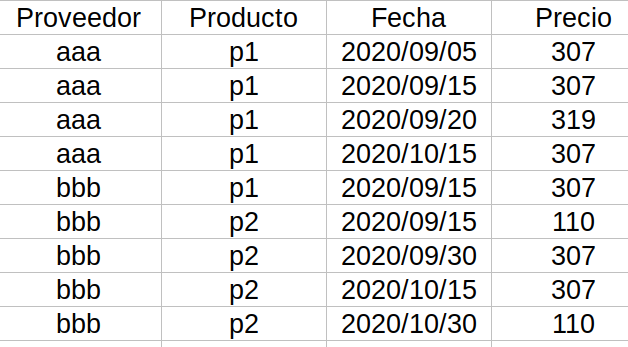
En nuestro caso el producto viene definido por 4 variables (también se incluyen variables que son parámetros pasados al proveedor pero que no tienen más relevancia que definir el producto por lo que no se mencionan.): la fecha del vuelo, el tipo de vuelo(business, regular), la ciudad de origen, el destino y los otros vuelos incluidos en la petición (esta variable se incluye ya que un vuelo podría tener varias escalas y las aerolíneas podrían ofrecer un descuento si se adquieren todas las secciones del viaje con la misma empresa).
Antes de usar el modelo hay que realizar un preprocesado de estos datos de forma que estén en un formato adecuado para el modelo. El objetivo del preprocesado es llevar los datos a un estado en el que cada fila sea un precio junto con la duración del mismo, lo que posibilita el uso del modelo AFT.
Además, la implementación en PySpark del AFT acepta datos solamente con truncamiento por la derecha por lo que hay que llevar los datos que tengan otro tipo de truncamiento a esta forma.
Como sólo observamos los precios en algunos instantes del tiempo, si asumimos que no hay otros cambios de precios entre nuestras observaciones, cada uno de los precios en nuestros datos es una observación con doble truncamiento por intervalos.
Por ejemplo, en la siguiente figura se representa cada una de las veces que hemos obtenido un precio para un cierto vuelo durante un cierto periodo. El precio 100 que observamos en los días 2 y 6 pudo haber comenzado como mínimo el día 1 ya que ese día obtuvimos un precio diferente. Además, el último día que pudo estar vigente es el día 10, por lo tanto, sabemos que el tiempo de duración de este precio es de 4 a 9 días.
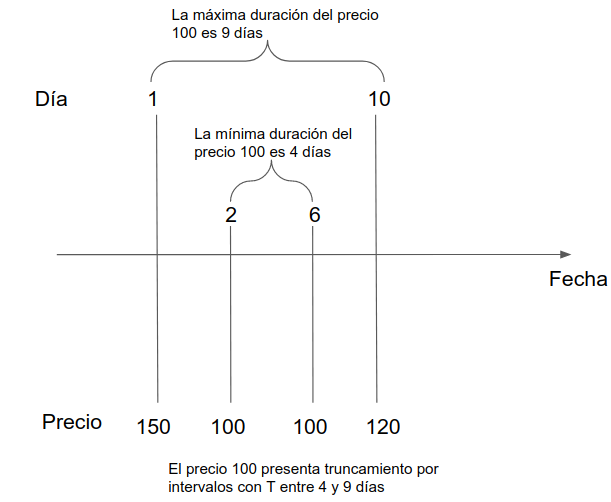
Aplicando este razonamiento a los datos de ejemplo del apartado anterior se obtiene una tabla como la siguiente:

El siguiente paso es utilizar el intervalo [𝛵𝜄, 𝛵𝑢] de la variable𝛵 para obtener un único tiempo de duración del precio con el cual alimentar el modelo. En la literatura se suele usar el punto medio del intervalo para obtener una única variable de duración, así que aplicamos este método a las observaciones que tienen todos los límites de tiempo definidos. En el caso de aquellos con truncamiento por la derecha, agregamos una variable que nos indica que este truncamiento existe. Las observaciones con límite inferior igual a cero no nos dan información relevante ya que es todo el intervalo de la variable duración por lo que descartamos estas observaciones.
La tabla final que utilizaremos para entrenar el modelo tiene la siguiente forma:

Un dato importante que vale la pena recalcar es que para la implementación de AFT de PySpark la variable que indica el truncamiento “censor” tiene el valor cero cuando la observación está truncada por la derecha y uno cuando no lo está.
Con esta tabla podemos crear el modelo en Spark. Hay que tener en cuenta que en PySpark no es posible obtener la curva de supervivencia a partir de un modelo entrenado de AFT. Sin embargo, es posible proporcionar al modelo un vector de cuantiles que deseemos de la curva de supervivencia. Por ejemplo, si estimamos el modelo con un vector cuyo único elemento es 0,5 entonces al realizar predicciones, además del tiempo promedio, es posible obtener el día en el cual la probabilidad de supervivencia alcanza ese valor. Para aproximar toda la curva de supervivencia podemos utilizar luego una función que interpole entre los cuantiles con los que hayamos entrenado el modelo.
El código para entrenar el modelo con los datos simulados que veníamos utilizando es:
import org.apache.spark.ml.linalg.Vectors
import org.apache.spark.ml.regression.AFTSurvivalRegression
# Label = tiempo que el precio de un boleto es válido
# vectors = variables explicativas = ['tiempo hasta que salga el vuelo', 'el vuelo es business']
training = spark.createDataFrame([
(10, 0.0, Vectors.dense(50, 0)),
(15, 1.0, Vectors.dense(180, 0)),
(30, 1.0, Vectors.dense(200, 1)),
(12, 1.0, Vectors.dense(60, 0)),
(20, 0.0, Vectors.dense(45, 1))], ["label", "censor", "features"])
quantileProbabilities = [0.3, 0.6]
aft = AFTSurvivalRegression(quantileProbabilities=quantileProbabilities,
quantilesCol="quantiles")
model = aft.fit(training)
# Imprimimos coeficientes
print("Coefficients: " + str(model.coefficients))
print("Intercept: " + str(model.intercept))
print("Scale: " + str(model.scale))
# Hacemos predicciones sobre los datos de entrenamiento
# Aquí nos devuelve una columna con los tiempos en los que se alcanza
# una probabilidad de supervivencia igual a 0.3 y 0.6 (colocadas en quantileProbabilities)
model.transform(training).show(truncate=False)Conlcusión
En este post hemos visto conceptos básicos del análisis de supervivencia y hemos demostrado todo el proceso para transformar datos de negocio en datos que encajan en el modelo de AFT implementado en PySpark. La idea principal es que al leer estas líneas te plantees el uso de esta herramienta como una forma adicional para resolver los problemas que enfrentan ciertas empresas.
Si te ha parecido útil este post, te animamos a ver más artículos como este en la categoría Data Analytics en nuestro blog y a compartirlo con tus contactos para que ellos también puedan leerlo y opinar. ¡Nos vemos en redes!

