En el post de hoy trataremos desde otro punto de vista uno de los juegos más populares que se pueden realizar a papel, el Sudoku. El objetivo será explicar un algoritmo para la resolución del mismo, junto con el código que nos permitirá solucionarlo. Comenzaremos con una pequeña introducción de las reglas de este juego, por lo que si ya las conoces siéntete libre de pasar a la siguiente sección.
Reglas del Sudoku
A priori, las reglas de este juego son sencillas:
- Partiendo de un tablero formado por 9 filas y 9 columnas debemos rellenar todas las casillas con números del 1 al 9.
- Las casillas se deben rellenar de manera que cada fila, bloque o columna del sudoku, contenga todos los números del 1 al 9 sin repetir.
Además, nos referiremos a las celdas del Sudoku como un par de valores que indican la posición de su fila y columna respectivamente. De esta forma, cuando nos referimos a la celda (2, 8), debemos dirigirnos a la celda de la segunda fila y octava columna.
Por último, destacar que un Sudoku bien construido tiene una solución única. Esto es posible gracias a que partimos de ciertos valores en el Sudoku los cuales nos permiten ir completando celdas hasta rellenar todas.
Método de resolución
A la hora de enfrentarnos a un Sudoku, proponemos tres enfoques lógicos distintos para su resolución. Para explorarlos, comenzaremos con un Sudoku y aplicaremos diversas técnicas para resolverlo.
Basic Filler
Dada una celda de un tablero, conocemos las 3 condiciones que debe complir un número para ser un candidato a rellenar la celda. El número debe de ser único en la fila, en la columna y en el bloque.
De esta forma, tenemos un conjunto de soluciones factibles por fila (F), columna (C) y bloque (B). La intersección de estos tres conjuntos nos dará el conjunto de soluciones posibles para una celda. Cuando dicho conjunto cuenta únicamente con un elemento, entonces la única solución posible es dicho elemento, por lo que podríamos cubrir la celda con él.
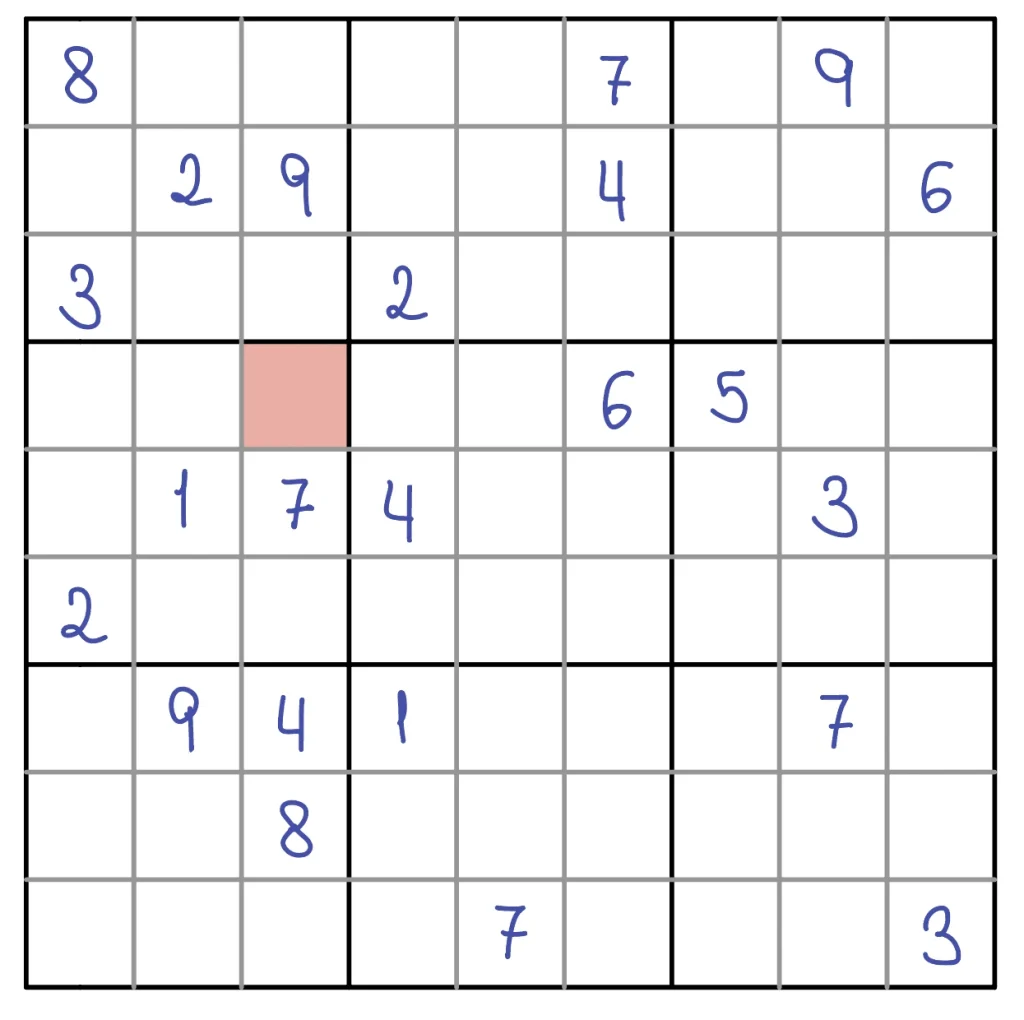
Ejemplo: Dada la imagen superior, nos fijaremos en la celda marcada en rojo. En esta celda, los conjuntos de soluciones factibles son:
- F = {1, 2, 3, 4, 7, 8, 9}
- C = {1, 2, 3, 5, 6}
- B = {3, 4, 5, 6, 8, 9}
De esta forma, la intersección de los tres conjuntos será F ∩ C ∩ B = {3}. Como la única solución factible es 3, rellenamos la celda con el número 3.
Deep Filler
La anterior mecánica podría no servir para completar todas las celdas del Sudoku. En este escenario, para completar una celda, utilizaremos la información de las celdas de su misma fila, columna o bloque.
Realizaremos esto de la siguiente forma: dada una fila/columna/bloque, si sabemos que un número es factible en una celda y no es factible en ninguna celda más de su misma fila/columna/bloque, entonces ese número tiene que completar esa celda.
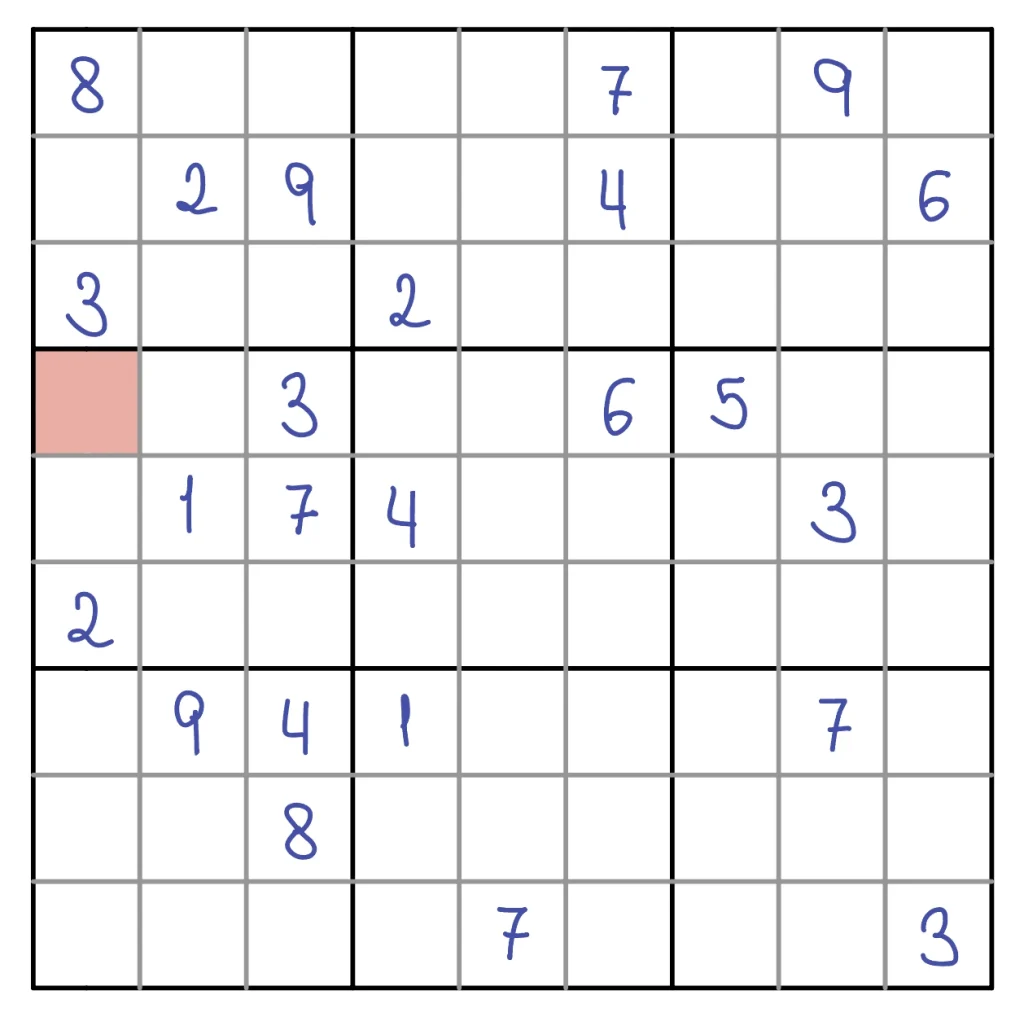
Ejemplo: Continuando con el anterior Sudoku, ahora completaremos la celda de la cuarta fila y primera columna. Los conjuntos de soluciones factibles para las celdas no completadas de la primera columna son:
- (2, 1): {1, 5, 7}
- (4, 1): {4, 9}
- (5, 1): {5, 6, 9}
- (7, 1): {5, 6}
- (8, 1): {1, 5, 6, 7}
- (9, 1): {1, 5, 6}
Como podemos ver, en la primera columna, la única celda que admite como solución el número 4 es (4, 1). Debido a que es un requisito que todas las columnas contengan todos los números, entonces rellenamos la celda (4, 1) con el número 4.
Guess Filler
Por último, evaluaremos el escenario en el que no es posible completar ninguna de las celdas utilizando los métodos anteriores. Cuando esto ocurra, buscaremos la celda incompleta con el menor número de soluciones factibles y llevaremos a cabo una solución muy humana, probar una de las opciones seleccionada arbitrariamente.
Esto nos permitirá seguir completando el resto de celdas del Sudoku. Si llegamos a una situación en la que no se pueda completar una celda sin incumplir las normas del Sudoku, entonces sabremos que la opción tomada anteriormente es incorrecta. De esta forma, podemos probar las diferentes opciones de una celda hasta llegar a la solución correcta.
Cabe la posibilidad de que, tras haber seleccionado un valor utilizando el método Guess Filler, sea necesario volver a utilizarlo. Esto provocaría tener que explorar cada una de las alternativas hasta llegar a la solución correcta.
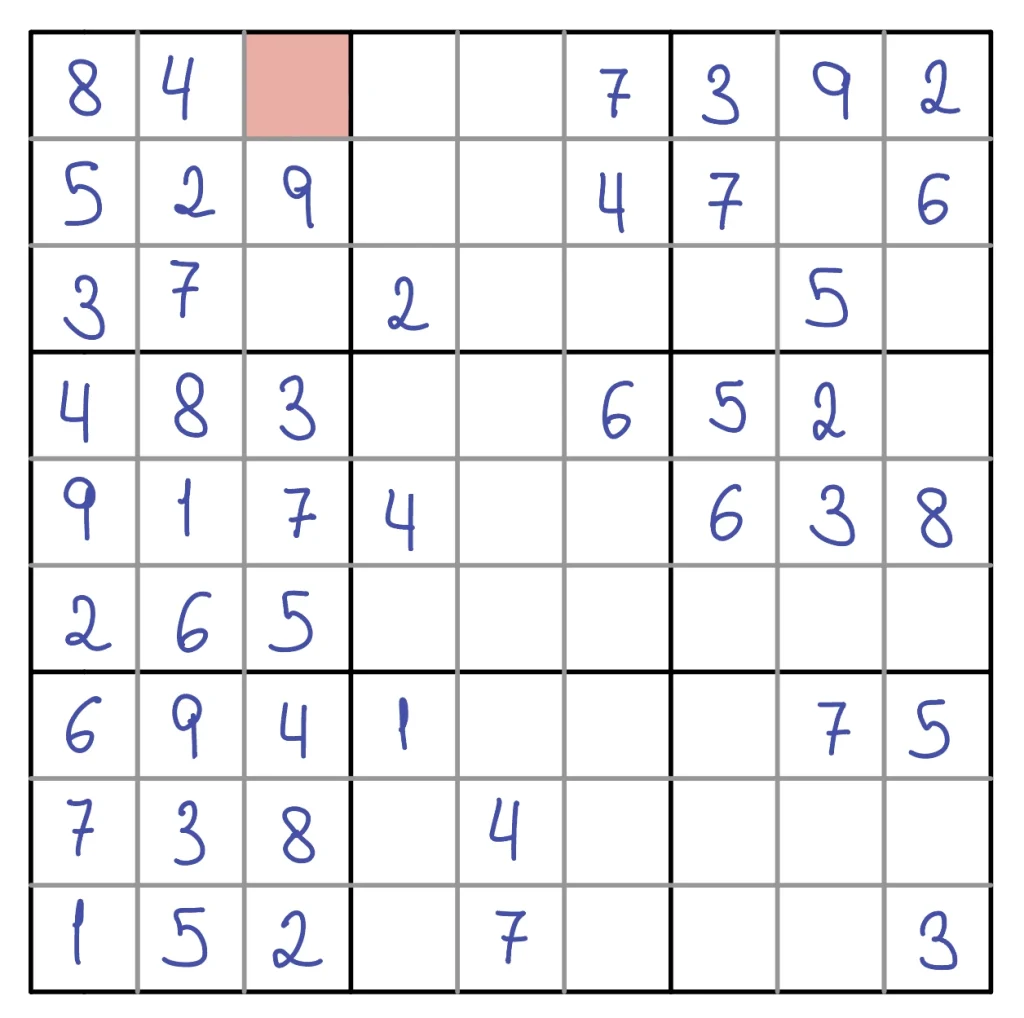
Ejemplo: Hemos seguido desarrollando el sudoku anterior hasta que hemos llegado a la situación que vemos en la imagen superior. En este caso, no podemos aplicar ni el Basic Filler ni el Deep Filler para completar ninguna de las casillas. Para seguir avanzando en la solución del Sudoku haremos lo siguiente.
- Buscaremos una de las celdas con un mínimo de soluciones factibles. En este caso la celda (1, 3) tiene como posibles soluciones el conjunto {1, 6}, siendo esta una de las celdas con un menor número de soluciones factibles.
- Seleccionaremos arbitrariamente una de las opciones y seguiremos completando el sudoku. Supongamos que en este caso tomamos el número 6.
- Continuamos completando el Sudoku hasta el final. En caso de encontrar una celda sin ninguna solución posible, volveremos al anterior tablero y seleccionaremos la otra alternativa.
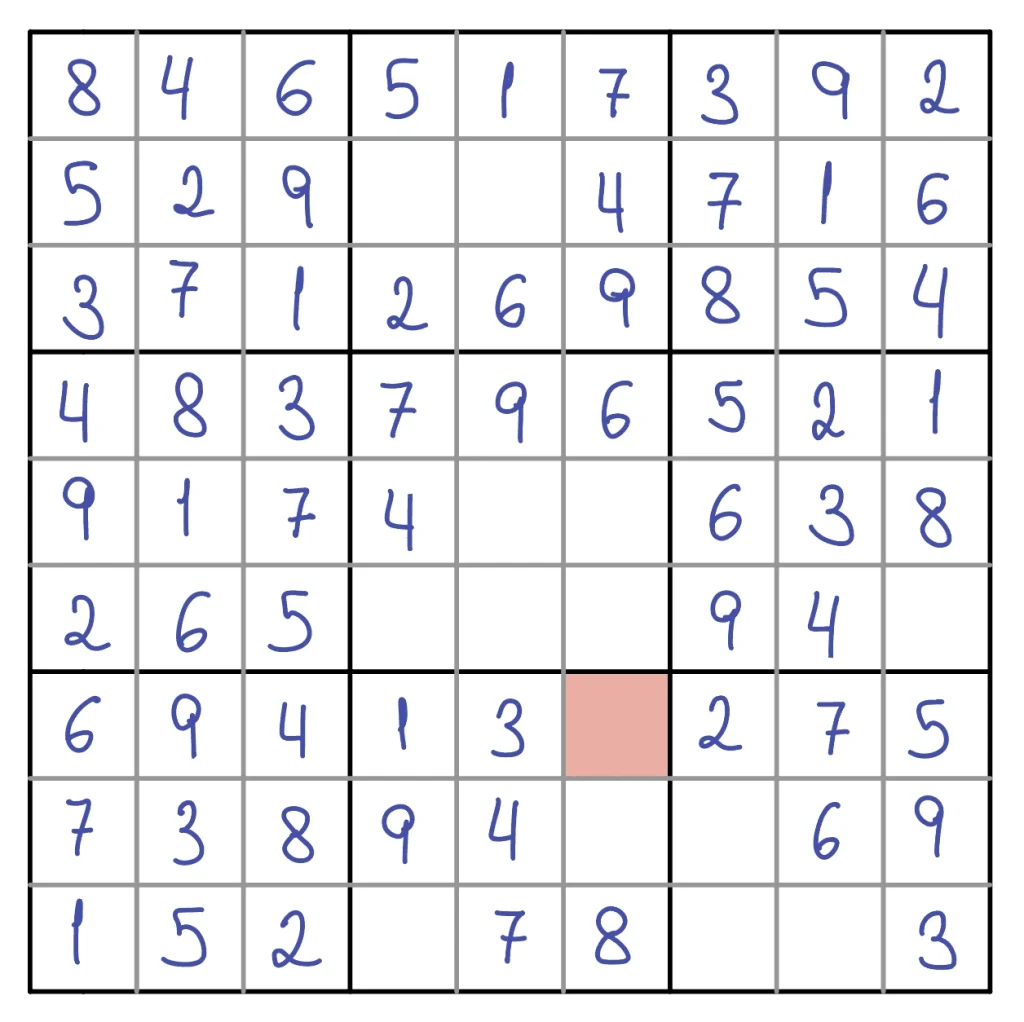
En este caso, tomando el número 6 en la casilla (1, 3), llegamos al tablero que podemos encontrar en la imagen inferior. Como podemos ver, la casilla situada en la posición (7, 6) no tiene ninguna solución posible. De esta forma, descartamos el 6 como posible solución de la celda (1, 3) y nos quedaremos con el 1.
Algoritmo para la resolución de sudokus
- Basic Filler:
- Recorremos todas las celdas del tablero buscando las soluciones factibles para cada celda.
- En aquellas celdas en las que la solución esté formada por un único número, rellenaremos dichas celdas.
- Si se ha completado al menos una celda, avanzamos hasta el Paso 4 (Comprobaciones). En caso de no completar ninguna pasaremos al Paso 2 (Deep Filler).
- Deep Filler:
- Recorreremos de nuevo todas las celdas del tablero, pero en este caso utilizando las soluciones factibles de las celdas vecinas para completar una celda.
- En caso de rellenar al menos una celda, avanzamos hasta el Paso 4 (Comprobaciones). En caso contrario, pasaremos al Paso 3 (Guess Filler).
- Guess Filler:
- Comenzaremos buscando una celda con un conjunto mínimo de posibles soluciones.
- Tras ello, realizaremos una copia de seguridad del tablero y de las posibles soluciones de la celda.
- Tomaremos uno de los posibles valores de la celda.
- Avanzamos al Paso 4 (Comprobaciones).
- Comprobaciones:
- Comprobamos si la actual solución es válida y, en caso de que así sea, regresamos al Paso 1 (Basic Filler).
- En el escenario en el que la solución sea inválida, podrían ocurrir dos alternativas. Si tenemos alguna copia de seguridad del tablero tomada cuando hicimos backtracking, volveremos a la última copia y regresamos al Paso 1 (Basic Filler). En caso de no tener ninguna copia de seguridad, concluimos que el Sudoku es irresoluble y damos el algoritmo por terminado.
Backtracking
A la técnica utilizada en el Paso 3 del algoritmo se la conoce como backtracking. Se suele utilizar en situaciones donde se deben explorar diversas opciones para encontrar una solución viable. De esta forma, iremos probando las diferentes soluciones y retrocederemos cuando la rama particular no lleve a la solución deseada.
El proceso de backtracking se implementa a través de una búsqueda en profundidad en un árbol de posibles soluciones, donde cada nodo representa una decisión y cada rama representa una opción. Cuando se alcanza un punto en el que no hay soluciones viables en una rama determinada, el algoritmo retrocede al nodo anterior y explora otras ramas.
Además, en el algoritmo propuesto, hemos acotado la complejidad del árbol al utilizar el Basic Filler y el Deep Filler para completar la mayoría de las celdas. Como resultado, el algoritmo propuesto es más del doble de rápido que si únicamente utilizamos backtracking.
Implementación
Podemos encontrar la implementación del Solucionador de Sudokus descrito en este artículo en el siguiente link de Github.
Próximos pasos
Una posible mejora a este proyecto sería generalizar la resolución de los Sudokus. Esto se podría realizar para aquellas dimensiones en las que el tamaño del tablero sea de dimensiones n x n, donde n es un número natural (en el caso particular de este artículo, n es igual a 9). Bajo estas condiciones, los números con los que se completaría el Sudoku irían desde el 1 hasta el n. También se podrían plantear mejoras en el aspecto de la eficiencia, tratando de reducir el tiempo de resolución de cada uno de los Sudokus. Por último, dado un Sudoku con más de una solución válida, se podría implementar que devolviese todas ellas.
Conclusión
En este recorrido, hemos explorado la resolución del Sudoku a través de métodos como Basic Filler, Deep Filler y Guess Filler. Además, hemos desglosado estratégicamente el proceso para abordar tanto situaciones simples como casos más complejos.
El Sudoku ha demostrado ser un campo fértil para la aplicación de algoritmos y estrategias lógicas. Desde el Basic Filler, el cual busca soluciones únicas en filas, columnas y bloques, hasta llegar al Guess Filler, que nos permite explorar opciones, retroceder cuando es necesario y avanzar hacia la solución final.
La combinación de estos métodos no solo demuestra su eficacia, sino que también destaca la importancia de elegir enfoques específicos según la complejidad del problema. Al acotar la complejidad del árbol de decisión mediante estrategias más simples, hemos logrado un algoritmo más eficiente y rápido. De hecho, los métodos implementados están basados en estrategias que los humanos utilizan normalmente para resolver Sudokus, mostrando que en muchos casos, la intuición humana es un buen punto de partida.
En última instancia, este trabajo resalta cómo la aplicación inteligente de algoritmos puede tener un impacto significativo en la resolución de problemas complejos. Desde los juegos de mesa hasta la informática, la elección correcta de algoritmos no solo acorta los tiempos de resolución, sino que también allana el camino para abordar desafíos de manera eficiente y efectiva.
