La capacidad de recolectar y procesar grandes cantidades de datos representa un valor adicional para muchas empresas en el mercado actual. El mundo del deporte no ha sido una excepción, empezando por el béisbol con la irrupción del SABRmetrics en en la década de los 80, pasando por el automovilismo hasta llegar a deportes como el baloncesto y el fútbol más recientemente. La creación de modelos y métricas mediante la inteligencia artificial permite a aficionados del deporte analizar el juego desde otra perspectiva y, a sus profesionales, adquirir una ventaja competitiva respecto a sus rivales.
En el caso del fútbol, probablemente la métrica más popular es la que se conoce como expected goal (xG). El xG pretende medir la probabilidad a priori de que un disparo acabe en gol, tomando en cuenta variables como la posición del disparo, la posición del portero o la parte del cuerpo con la que se dispara. Al ser una probabilidad, debe tomar valores entre 0 y 1, de manera que para las oportunidades más claras (por ejemplo, un disparo dentro del área pequeña sin portero) tome valores cercanos a 1, y para los tiros más alejados o con mayor dificultad tienda a 0.
Esta métrica es muy útil para los cuerpos técnicos y equipos de scouting para evaluar la capacidad de finalización o de creación de oportunidades de los distintos jugadores. Así, por ejemplo, si miramos la diferencia entre el número de goles que ha marcado un jugador y la suma de los xG de los tiros que ha realizado, una diferencia positiva o negativa indicará, respectivamente, una alta o baja capacidad de finalización del jugador. Del mismo modo, si los pases de un jugador dan lugar a disparos de alto xG, esto indica que es capaz de crear ocasiones de gol claras.
Cada usuario genera su modelo de xG a partir de la información disponible que considera más relevante, en búsqueda de que la probabilidad emitida se ajuste de la manera más precisa posible al histórico de disparos que se tiene.
El presente estudio se basa en datos de Wyscout, uno de los mayores proveedores de datos de fútbol, que recoge información de todos los eventos que ocurren en cada partido. Se dispone de un conjunto de datos de unos 8.500.000 registros de eventos, conteniendo variables como la liga o el partido de que se trata, el jugador que lo protagoniza, el tipo de evento (disparo, pase, robo de balón, etc.) o su posición en el campo, entre otras.
De esos, unos 117.000 registros son disparos, y son en los que se centrará nuestro modelo de xG. Estos eventos corresponden a 25 competiciones profesionales de clubes de Europa y América (ligas nacionales y Copa Libertadores), en su mayoría de la edición 2020/21 (2021 en LATAM y USA).
Consideraciones iniciales
- La métrica xG pretende evaluar la peligrosidad de un disparo en el momento inmediatamente anterior a la ejecución del mismo. Por tanto, no se puede introducir en el modelo información que sea posterior a la ejecución del disparo, tal como si el disparo fue bloqueado o si el portero se venció a un lado. De esta manera, el valor devuelto como la probabilidad a priori de que dicha acción termine en gol.
- El xG tiene como objetivo, entre otros, poder valorar la habilidad de los jugadores de crear oportunidades de gol (pasadores), transformarlas (rematadores) o evitarlas (defensores). Como tal, dicho valor debe reflejar la probabilidad genérica de que en ciertas condiciones fijadas un disparo termine en gol, y por tanto abstraerse de condiciones específicas como cuáles son los equipos atacante y defensor, los jugadores involucrados o sus demarcaciones, así como la liga, la fecha o el lugar en el que se produce.
- Cada acción del partido es etiquetada con una serie de valoraciones por los analistas de Wyscout. Estas representan información más o menos subjetiva, como por ejemplo si el pase precedente al disparo es un pase filtrado, o si la acción constituye una oportunidad de gol. Suponemos que a la hora de emplear el modelo, al igual que durante su entrenamiento, el usuario final tendrá acceso a dicha información. Notemos que, con la hipótesis de que el etiquetado siga un criterio uniforme e imparcial (por ejemplo, que el hecho de etiquetar un disparo como oportunidad clara o no, no dependa del jugador que está disparando), esta información no contradice el principio de generalidad anteriormente mencionado, ya que dos acciones idénticas protagonizadas por dos jugadores distintos tendrán exactamente el mismo conjunto de variables de entrada y, por tanto, el mismo valor de xG. Por tanto, introducimos también variables subjetivas en nuestro modelo, como lo hace Wyscout en su propio modelo de xG.
Desarrollo del trabajo
Notemos que lo que se quiere predecir es si un disparo será o no gol, por lo que nos enfrentamos a un problema de clasificación binaria.
Para empezar realizamos un análisis exploratorio de los datos disponibles en el que estudiamos los datos, los valores inesperados y realizamos ingeniería de variables para enriquecer nuestro dataset.
En segundo lugar, procederemos a realizar una selección de variables en base a distintos criterios, y sobre cada uno de estos conjuntos de datos ajustaremos distintos modelos supervisados. A continuación, compararemos sus resultados para así encontrar el modelo y su combinación de hiperparámetros óptimos para la tarea de clasificación.
Finalmente, evaluaremos el mejor modelo sobre un conjunto de datos no vistos anteriormente para probar su capacidad de generalización, usando como benchmark el propio valor del xG calculado por Wyscout, que proporciona junto con el dataset de eventos.
Análisis exploratorio de datos
En esta fase, analizamos los datos y realizamos el preprocesado necesario. Para empezar, vemos que nuestro conjunto de datos inicial contiene eventos de tipo ‘penalty’ (tiro penal), ‘free_kick’ (tiro libre) o ‘shot’ (tiro en jugada).


Es habitual a la hora de realizar modelos de xG descartar los tiros de penal puesto que son acciones muy aisladas del juego y con condiciones muy particulares. Por tanto, entrenamos nuestro modelo únicamente con los registros de tiros libres y disparos en jugada. Tras este filtro, contamos con 115,152 registros de disparos.


Asimismo, vemos que las clases que queremos predecir (‘Gol’ o ‘Fallo’) están muy desbalanceadas, con una proporción aproximada de 1 gol por cada 9 fallos. En este punto, podríamos considerar métodos para balancear las clases, como por ejemplo usar data augmentation o reducir el número de registros de la clase ‘Fallo’. Sin embargo, creemos que el primero es peligroso pues hemos observado que una pequeña modificación en un parámetro puede ser diferencial para el resultado del disparo. Por otro lado, la segunda opción implicaría reducir el volumen del dataset a unos 20.000 registros, lo que consideramos un número demasiado bajo para entrenar un modelo de clasificación.
Por otro lado, las variables que hacen referencia al tipo de posesión (contraataque, jugada de balón parado, etc.) o el tipo de subevento (recuperación tras presión, pase clave, etc.), tanto para el evento actual como los anteriores, contienen una lista de valores, por lo que creamos una variable binaria para cada valor posible e indicamos con un 0 o un 1 si cada evento lo contiene (notemos que cada fila puede tener más de un 1, por lo que no es un one-hot encoding).
En algunos casos, estos valores son subjetivos ya que han sido etiquetadas por un humano (por ejemplo, “pase filtrado” para el evento anterior u “oportunidad de gol” para el disparo), pero como hemos comentado en el apartado de Consideraciones iniciales, decidimos usarlos de todos modos.
Siguiendo con dicho apartado, a continuación descartamos todas las variables que no pueden determinarse en el momento del disparo, ya que es entonces cuando debe calcularse el xG. Así, por ejemplo, no introducimos en el modelo si es un disparo bloqueado o si va a puerta. Del mismo modo, se descartan las variables específicas del contexto, tales como la demarcación, el equipo o la liga en la que juega el lanzador, o bien métricas sobre el portero. Como se ha explicado, si bien podría mejorar al modelo actual en cuanto a capacidad predictiva, el resultado que se obtendría con tales variables no podría interpretarse como un xG.
La siguiente fase del proceso es la ingeniería de variables. Para empezar, se eliminan los valores nulos o anómalos (tales como una distancia negativa), sustituyéndolos por la media de la variable numérica en cuestión para no introducir sesgo en el modelo. Asimismo, recuperamos información diversa que puede ser útil para la tarea de clasificación, tal como los 3 eventos inmediatamente anteriores al evento de disparo, de los cuales recogemos su posición en el campo, el tipo de evento (duelo, pase, saque de banda, etc.) o cuántos segundos antes del disparo ocurrió dicha acción, entre otras variables.
A continuación, se crearon nuevas variables a partir de las ya existentes. Por ejemplo, la posición (X,Y) del disparo (ambas normalizadas entre 0 y 100) se sustituyó por la distancia al centro de la portería o el ángulo de disparo, por considerarse más significativas. Asimismo, se calculó si ocurrió un cambio de posesión en las tres acciones inmediatamente anteriores.



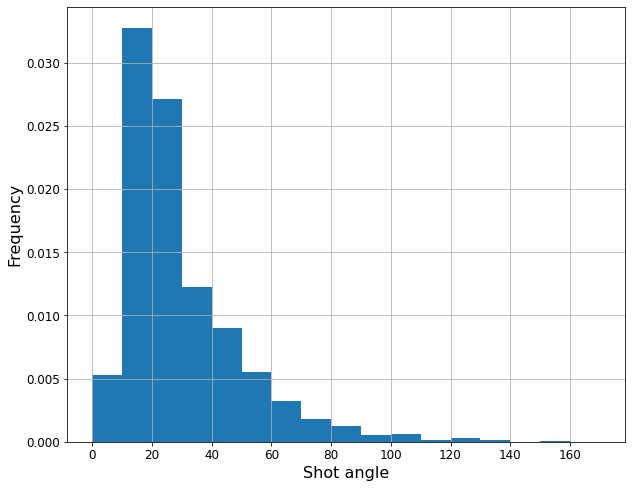
Para terminar, se realizó one hot encoding de las variables categóricas, como por ejemplo la parte del cuerpo con la que se dispara (pierna derecha, izquierda, u otro) o el tipo de evento, tanto actual (un tiro libre o en jugada) como el anterior (duelo, pase, parada, etc.).
Selección de variables
Tras la fase anterior, contamos con 309 variables, muchas de ellas binarias. Al ser un número muy elevado teniendo en cuenta el número de registros disponibles, se decidió usar solamente un subconjunto de estas para entrenar los modelos predictivos. Para la selección de variables se consideraron distintos métodos.
- Variables especificadas en la documentación del propio modelo de xG de WyScout. Como no se especifican todas las variables usadas, se añadieron otras variables ampliamente usadas en otros modelos de xG, con un total de 15 variables.
- Variables con una correlación lineal con respecto a la variable dependiente superior a un umbral de 0.1 (en valor absoluto), con un total de 27 variables.
- Variables seleccionadas mediante el método de Boruta. Este método consiste en ejecutar un conjunto de N random forests sobre la unión del conjunto de variables originales y un conjunto de shadow variables, consistentes en la permutación aleatoria de los valores de las variables originales. Finalmente, sólo se seleccionan aquellas variables cuyo índice de Gini, o poder explicativo sobre la variable dependiente, se encuentra por encima de cierto percentil prefijado con respecto a las shadow variables. De esta manera nos quedamos con las variables significantes y descartamos las variables que no aportan información valiosa para la clasificación.
En este caso, se han usado N=100 random forests, cada uno con T=413 árboles (número de árboles elegido automáticamente a partir de la longitud del dataset) con una profundidad máxima de 5, y usamos el percentil 100 (nos quedamos sólo con las variables que superen en poder explicativo a todas las versiones aleatorizadas). Nos quedamos así con 79 variables.
Preparación de los datos
A continuación, dividimos el conjunto de datos en train y test, con una proporción de 80% y 20% y usando estratificación con respecto a la variable objetivo, esto es, conservando la proporción de goles y fallos en ambos conjuntos para poder evaluar correctamente el modelo. El conjunto de test no se usará durante el entrenamiento ni la elección del modelo, ya que representa un conjunto de datos del que no se dispone de entrada, y se usará simplemente para evaluar la capacidad de generalización del modelo final sobre un conjunto de datos no visto.
Posteriormente, realizamos un escalado estándar (entre 0 y 1) para toda variable independiente no binaria, tal como el ángulo del disparo o el tiempo transcurrido desde la acción anterior.
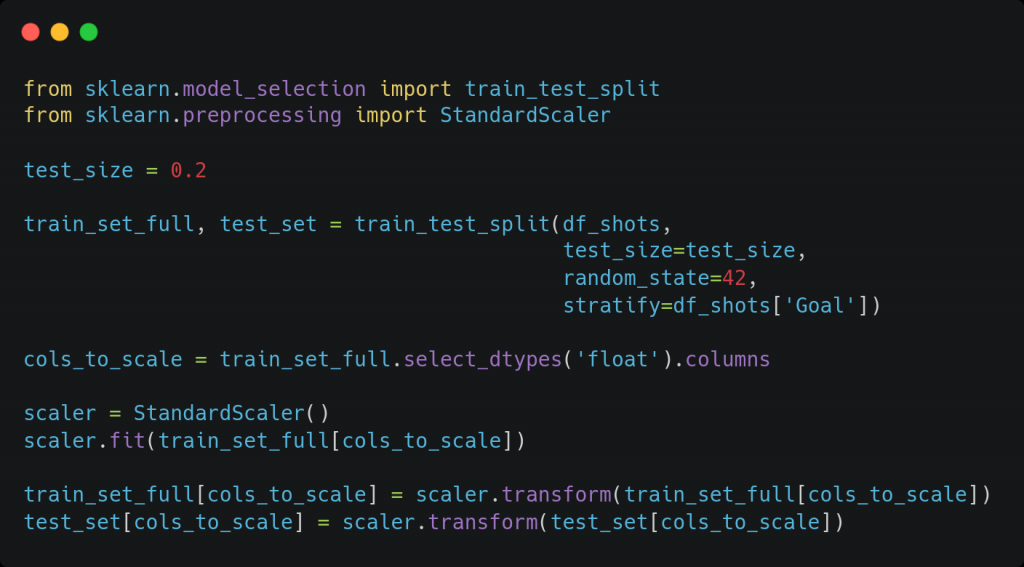
Notemos que se realiza el mismo escalado tanto para el conjunto de entrenamiento como el de test, para evitar que las características particulares del conjunto de datos puedan alterar la decisión del modelo. En particular, escalamos todos los datos en base a la media y la desviación estándar del conjunto de entrenamiento, puesto que el conjunto de test representa unos datos no conocidos a priori.
Entrenamiento y comparación de modelos
Finalmente, procedemos al desarrollo de distintos modelos de clasificación, para lo cual se usan las librerías de scikit-learn y keras, entre otras. Cada uno de estos modelos será entrenado y evaluado sobre cada subconjunto de variables seleccionado previamente para encontrar la mejor combinación. Asimismo, se realizará un grid search para tratar de refinar los hiperparámetros del modelo en cada caso. Tanto durante el entrenamiento (grid search) como en la evaluación del modelo usando la mejor combinación de hiperparámetros, se usa validación cruzada de 10 iteraciones con una semilla fijada y de nuevo con estratificación, a fin de evaluar todos los modelos bajo las mismas condiciones.
Los modelos que se han considerado y algunos de los hiperparámetros que se han optimizado en el correspondiente grid search son los siguientes.
- Regresión logística: forma de regularización (L1, L2), parámetro de regularización, algoritmo de optimización.
- Random forest: número de árboles, número de variables en cada nodo, profundidad máxima de los árboles, etc.
- XGBoost: ratio de aprendizaje, profundidad máxima de los árboles, peso relativo de la clase positiva (para conjuntos de datos desbalanceados), etc.
- Red neuronal (perceptrón multicapa): ratio de dropout, estructuras con distinto número de capas y neuronas por capa, función de activación en las capas ocultas (en la capa de salida siempre se usa la función logística), algoritmo de optimización, etc.
Para prevenir el overfitting, en el caso del XGBoost, paramos el entrenamiento cuando, tras añadir 10 árboles, la función de pérdidas sobre el conjunto de validación no disminuye. En la red neuronal, paramos el entrenamiento al aumentar la función de pérdidas sobre el conjunto de validación en dos epochs consecutivas. En ambos casos usamos como función de pérdidas la entropía cruzada binaria.
La métrica elegida para comparar los modelos es el área bajo la curva ROC (ROC-AUC), comúnmente usada en problemas clasificación binaria cuando existe desbalanceamiento en las clases, como ocurre en nuestro caso. Así pues, buscaremos el modelo y la combinación de hiperparámetros que resulte en un mayor valor de ROC-AUC. La probabilidad emitida por este modelo será finalmente nuestro valor de xG.
Debido al elevado número de parámetros y el amplio rango de valores que se quiere estudiar, dividimos el grid search en dos pasos. En el primer paso se hace una búsqueda dentro de una amplia malla de valores para cada hiperparámetro, con el objetivo de obtener el orden de magnitud óptimo de cada uno. En este caso, para reducir el tiempo de entrenamiento, probamos solamente con una fracción de todas las combinaciones posibles usando la función RandomizedSearchCV de scikit-learn.
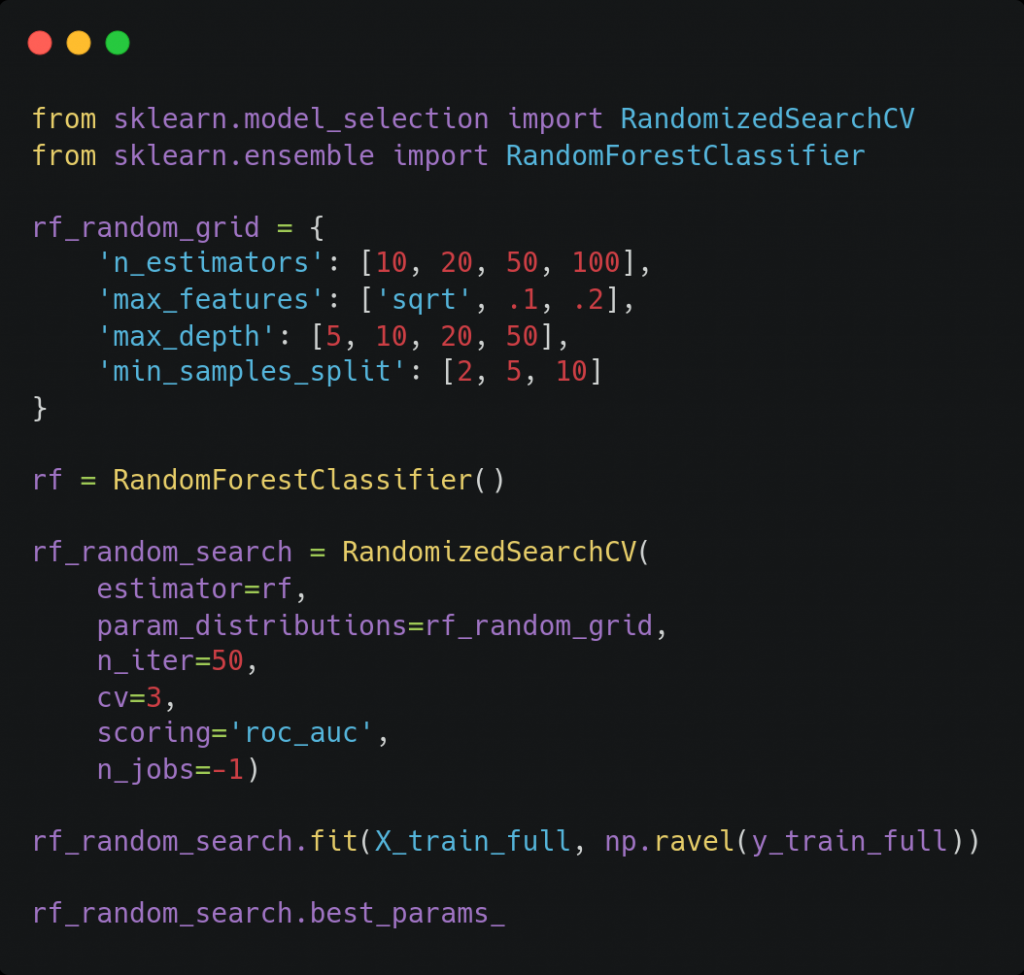

En el segundo paso, realizamos una búsqueda en un espacio más reducido donde esperamos encontrar el óptimo. Así, si el mejor valor para cierto hiperparámetro encontrado en el primer paso se dio para un valor no extremo del intervalo considerado, se fija un rango reducido y centrado en dicho valor. En cambio, si se dio para un máximo (o mínimo) del intervalo considerado, se expande la búsqueda a valores mayores (o menores) que dicho valor. Esta vez usamos la función GridSearchCV para probar todas las posibles combinaciones, al haber reducido el espacio de búsqueda.
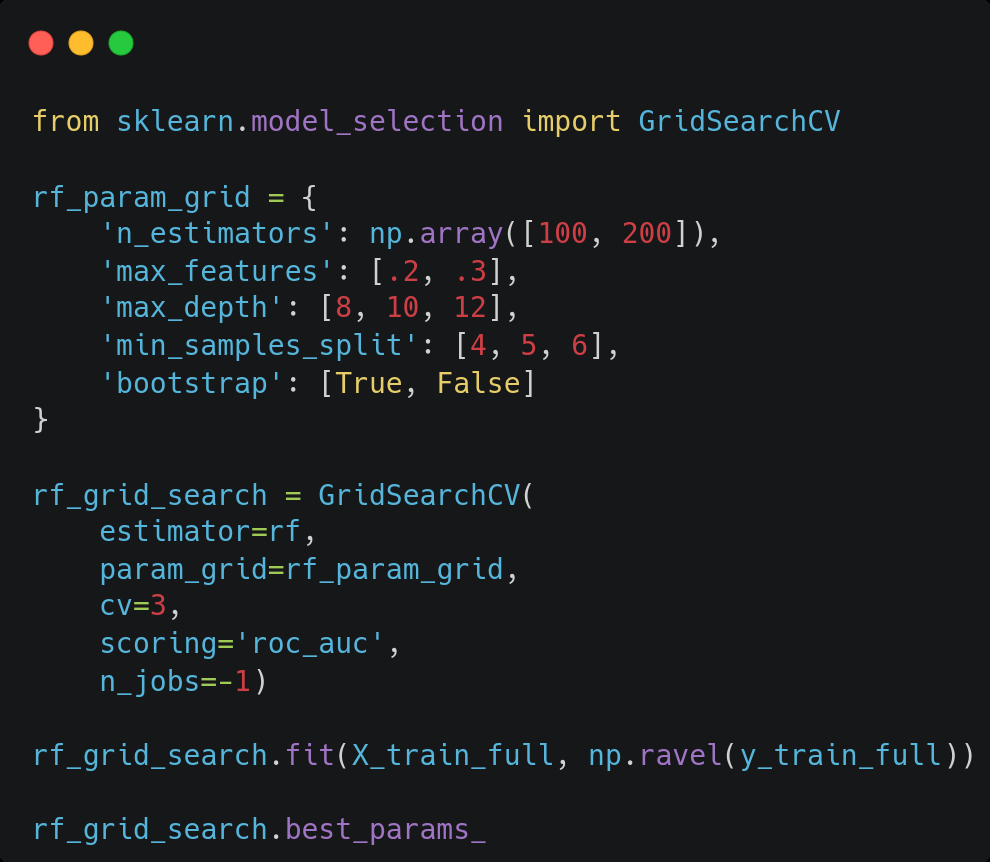

A continuación, evaluamos el modelo sobre el conjunto de entrenamiento usando la mejor combinación de hiperparámetros encontrada.
En la evaluación del modelo, se ha fijado la semilla para realizar la validación cruzada, de manera que todos los modelos sean entrenados y evaluados sobre los mismos subconjuntos de entrenamiento/validación y así evitar que la elección específica de estos favorezca a uno u otro modelo. Esta es la función para la evaluación del modelo para los modelos de scikit-learn.
Así, evaluamos el modelo con la mejor combinación de hiperparámetros encontrada anteriormente.


Finalmente, comparamos las métricas obtenidas para cada uno de los modelos. Los resultados obtenidos se muestran en la Figura 1.
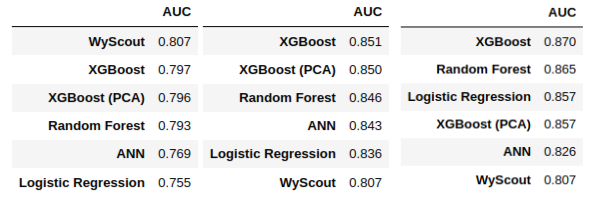
Como podemos ver, el mejor modelo obtenido en términos del valor del ROC-AUC ha sido el de XGBoost en todos los casos. Notemos que ha mejorado incluso a un modelo a priori más complejo como la red neuronal, probablemente debido al tamaño relativamente pequeño de nuestro dataset. En particular, el mejor resultado se ha obtenido al usar las variables seleccionadas mediante el método de Boruta.
Una vez fijado el mejor modelo y el mejor conjunto de variables de entrada, tratamos de mejorar los resultados del modelo aplicando análisis de componentes principales (PCA) a nuestros datos. Este método permite no solamente reducir la dimensionalidad y por tanto acelerar el proceso de aprendizaje de los modelos, sino que también puede favorecer su desempeño, al eliminar el posible ruido o redundancia de las distintas variables. Por ello, realizamos un nuevo grid search sobre un pipeline en el que aplicamos PCA con distintos números de componentes y, para cada caso, buscamos la combinación de hiperparámetros del XGBoost que mejor se ajusta a este conjunto de datos.
Finalmente, escogemos la mejor combinación de número de componentes principales e hiperparámetros del modelo, y lo evaluamos de nuevo. Comparamos las métricas obtenidas con las que se habían obtenido antes de realizar PCA para determinar si mejoran los resultados. En este caso, como se ve en la Figura 1, el desempeño del modelo en términos de ROC-AUC no aumenta al usar PCA. Este resultado da a entender que la ganancia que supone la eliminación del ruido y la redundancia al reducir la dimensionalidad no compensa la pérdida de información intrínseca en el proceso.
Notemos que se podrían probar diferentes combinaciones de número de componentes principales, tipo de modelo e hiperparámetros específicos del modelo. Asimismo, se podrían añadir al grid search del pipeline otras variables como el tipo de escalado de los datos. Sin embargo, consideramos que el espacio de búsqueda se hace demasiado grande para los intereses de este estudio, por lo que se ha fijado aquí el mejor tipo de algoritmo obtenido en el paso previo y tratado de mejorar su resultado mediante la aplicación de PCA.
Evaluación sobre el conjunto de test
Llega el momento de evaluar el desempeño sobre el conjunto de test del modelo escogido, para comprobar que es generalizable a conjuntos de datos no conocidos. Se ha comparado el ROC-AUC obtenido por nuestro modelo final con el que se obtiene con el xG proporcionado por Wyscout sobre este mismo conjunto, a modo de referencia. La Figura 3 muestra los resultados obtenidos.
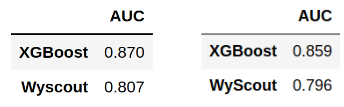
De manera coherente con los resultados obtenidos en la fase de análisis de los modelos, encontramos que con nuestro algoritmo se obtiene un valor de ROC-AUC mayor que el que arroja el modelo de xG de Wyscout para el mismo conjunto de datos.
Vemos que el valor del ROC-AUC de nuestro modelo sobre el conjunto de test es un 1.3% menor que el obtenido en la validación cruzada sobre el conjunto de entrenamiento, lo cual de entrada puede dar a entender que el modelo no ha sido capaz de generalizar a conjuntos de datos no conocidos. Sin embargo, observamos que el valor del ROC-AUC del modelo de Wyscout disminuye en un porcentaje similar (1.4%) sobre el conjunto de test con respecto al conjunto de entrenamiento.
Puesto que el modelo de Wyscout no ha sido entrenado con el mismo conjunto de datos que nuestro modelo, concluimos que no se trata de un problema de overfitting. Probablemente se deba al hecho de que dicho dataset contiene un número elevado de outliers, es decir, oportunidades de gol claras que son fallos, o bien registros de disparos con una baja probabilidad a priori de conversión que acaban en gol.
A continuación, comparamos las curvas ROC con uno y otro modelo. Esta curva muestra el ratio de verdaderos positivos (TPR) contra el ratio de falsos positivos (FPR) variando el valor del umbral específico para determinar si la clase predicha es ‘Gol’ o ‘Fallo’. Los valores de TPR y FPR se definen de la siguiente manera.
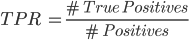
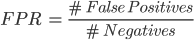
Vemos que el TPR mide la proporción de positivos (goles) correctamente predichos como tal, y el FPR mide la proporción de negativos (fallos) incorrectamente predichos como gol.
Así, para un umbral igual a 0, todos los disparos se predicen como ‘Gol’ ya que todas las probabilidades superan el umbral, por lo que tanto el TPR como el FPR son iguales a 1. En el otro extremo, un umbral igual a 1 resultaría en predecir todos los disparos como ‘Fallo’ ya que la probabilidad sería inferior al umbral en todo caso. Esto resultaría en un TPR y un FPR iguales a 0. Una clasificación perfecta consiste en aquella para las que se predice correctamente el resultado de todas las observaciones, por lo que el TPR es igual a 1 (no hay falsos negativos) y el FPR es igual a 0 (no hay falsos positivos).
En la Figura 4 se muestran las curvas ROC de ambos modelos de xG (el propio y el de Wyscout), considerando todos los umbrales desde 0 hasta 1 en intervalos de 0.01 para construir la curva ROC.
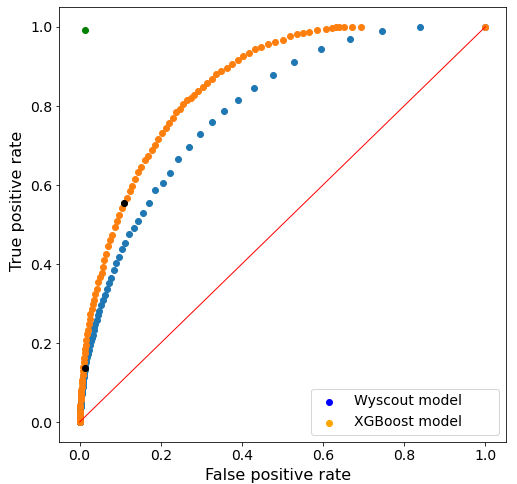
Como se puede observar, el modelo de Wyscout se desempeña notablemente mejor que una clasificación aleatoria, ya que está por encima de la línea que une los puntos (0,0) y (1,1). Sin embargo, con nuestro modelo se obtiene una mejor curva ROC en tanto que se encuentra más cerca del punto (0,1) óptimo, que correspondería a una clasificación perfecta.
Se observa asimismo que los resultados de la clasificación usando el umbral por defecto de 0.5 (representado por los puntos negros) difieren mucho en ambos casos. En particular, observamos que el modelo de Wyscout tiende a infravalorar las probabilidades de gol, resultando en un número elevado de falsos negativos (y por tanto un TPR alto) en comparación al número de falsos positivos (FPR bajo). Nuestro modelo, en cambio, tiende a predecir probabilidades más elevadas, por lo que se reduce el número de falsos negativos a expensas de aumentar el número de falsos positivos.
En la Figura 5 se comparan las matrices de confusión obtenidas con uno y otro modelo, que se construyen a partir del umbral de 0.5 explicado anteriormente.
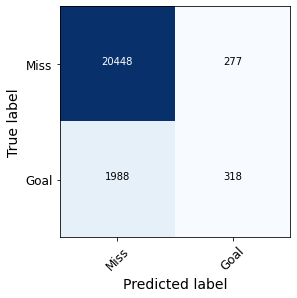
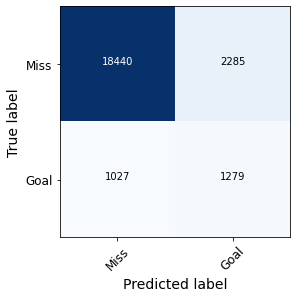
Figura 5. Matrices de confusión obtenidas con el modelo de Wyscout (izquierda) y el modelo propio (derecha).
En efecto, observamos como nuestro modelo produce un número de falsos positivos considerablemente mayor que el de Wyscout, mientras que el número de falsos negativos disminuye. En la Figura 6 se comparan los valores del recall, la precisión y la métrica F1 para la clase ‘Gol’ usando uno y otro modelo.
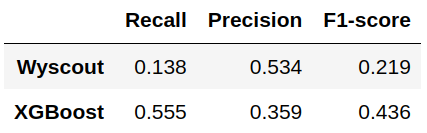
Como vemos, la precisión es menor en nuestro modelo debido al incremento de falsos positivos. Sin embargo, el recall es mucho mayor ya que se reduce drásticamente la proporción de falsos negativos en relación al número total de observaciones positivas. Ello hace que el valor del F1-score, que es la media armónica de las dos métricas anteriores, valga casi el doble en nuestro modelo que en el de Wyscout.
Conclusiones y trabajo futuro
Como mejoras a realizar sobre el trabajo, cabe comentar la posibilidad de probar con nuevos modelos de clasificación o nuevas combinaciones de hiperparámetros para los modelos usados. También se podrían usar diferentes tipos de escalados o PCA para cada uno de los modelos planteados junto con su correspondiente grid search en cada caso. Las posibilidades de estudio son infinitas y este trabajo representa solamente una manera de enfocar el problema.
Evidentemente, otro posible punto a mejorar sería la ingesta de datos, tanto en volumen (lo cual favorecería la convergencia de los modelos basados en redes neuronales), como en variedad (por ejemplo, tener información tal como la ubicación de los jugadores en el campo en el momento del disparo sin duda podría mejorar la performance de nuestro modelo).
Finalmente, una posible variación de este estudio consistiría en generar un modelo que tenga en cuenta variables que no hemos usado aquí, como información específica de los jugadores o equipos que intervienen en el disparo (estadísticas acumuladas en la temporada o rachas del jugador que dispara, del portero rival o de ambos equipos).
Si bien no se trataría de una métrica xG como tal, los resultados de este modelo permitirían evaluar de manera más realista el desempeño de un jugador o equipo en un contexto dado (por ejemplo, no es lo mismo enfrentarse a un portero mediocre que al mejor portero del mundo). De esta manera, dicha métrica podría servir para diseñar estrategias de juego específicas para cada jugador o situación del partido, y así adquirir una gran ventaja competitiva.
¡Esto es todo! Si este post te ha parecido interesante, te animamos a visitar la categoría Data Science para ver todos los posts relacionados y a compartirlo en redes. ¡Hasta pronto!

