Hungry Geese es una versión del mítico juego “Snake”, pero con gansos, de manera que múltiples agentes compiten entre sí con el objetivo de sobrevivir más tiempo. Este juego nace en una competición de Kaggle, desarrollada entre el 26 de enero de 2021 y el 10 de agosto de 2021. En él, los gansos no deben morir de hambre ni impactar contra los oponentes ni contra sí mismos. Una de las diferencias con el juego de “Snake” es que no hay límites por los bordes del tablero, por lo que cuando el ganso sale por uno de los 4 laterales, aparece por el contrario.
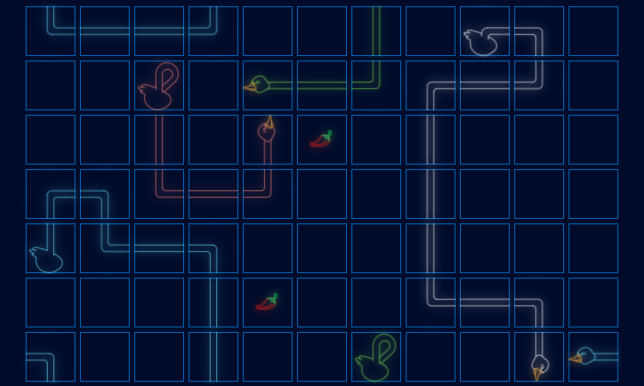
En este artículo se explicará cómo se ha implementado una inteligencia artificial básica con redes neuronales convolucionales que es capaz de competir a un buen nivel. Cabe destacar que este modelo no será superior a otro implementado mediante Reinforcement Learning, pero se pueden ver más rápidamente los resultados del entrenamiento realizado.
Reglas del juego
El objetivo es sobrevivir el mayor número de turnos alimentándose para mantenerse vivo y sin colisionar con tu propio ganso o el de otros agentes. La reglas del juego son las siguientes:
- Cuatro agentes compiten en un tablero de 11×7 celdas indicando en cada turno una de las siguientes acciones: NORTH, SOUTH, EAST o WEST.
- No está permitido hacer giros de 180º, es decir, volver a la casilla que se ocupaba en el turno anterior.
- Cada partida consta de 200 episodios. El agente con la valoración más alta o el último que sobreviva gana la partida.
- Si un agente se come una pieza de comida, se le añade un segmento a su cuerpo.
- Cada 40 episodios, el ganso pierde un segmento, independientemente de si ha comido o no con anterioridad.
- Los agentes deben tomar una decisión de movimiento en menos de 1 segundo. Si se sobrepasa, el tiempo de diferencia se añade a un contador. Si este contador llega a 60 segundos, el agente es eliminado de la partida.
Redes neuronales convolucionales con entrenamiento supervisado
Se han aplicado redes neuronales convolucionales con entrenamiento supervisado para crear una inteligencia artificial que pueda competir, sobre todo, con otros agentes implementados con algoritmos clásicos como Minimax o Monte Carlo Tree Search (MCTS).
Los modelos de inteligencia artificial supervisados requieren de un conjunto de datos de entrenamiento que contenga una “etiqueta” que indique cuál debería ser el resultado dadas unas variables. Para este caso, se han obtenido los conjuntos de datos de entrenamiento a partir de partidas reales extraídas mediante scraping al conjunto de metadatos de Kaggle.
Mediante esta técnica, se pueden obtener conjuntos de datos más fiables descargando las partidas de los mejores agentes (los de puntuación superior a 1200, los cuales han entrado en posiciones para obtener el oro) debido a que se presupone que sus acciones son las más correctas. No obstante, no son agentes perfectos y también pierden partidas o realizan jugadas que no son óptimas, por lo que en el conjunto de datos también se encuentran movimientos con acciones que no son 100% válidas y que el agente aprenderá de manera errónea.
Cabe mencionar que, en la competición, los que han conseguido una puntuación entre 1050 y 1080 han obtenido la medalla de bronce, los de 1080 a 1210 la de plata y a partir de 1210 la de oro, siendo de 1312 la puntuación que ha obtenido el ganador.
En el caso del juego Hungry Geese, las variables son el estado actual del tablero, es decir, las posiciones ocupadas por los cuerpos de cada agente, las posiciones ocupadas por comida o cualquier otro dato que dé información acerca del tablero. La “etiqueta” es la acción (NORTH, SOUTH, EAST o WEST) que se debería realizar dado un estado del tablero.
Hungry Geese es un juego en el que todos los jugadores deben moverse a la vez, a diferencia de otros donde cada jugador tiene su turno para decidir un movimiento.
Esto provoca que cada jugador deba decidir al mismo tiempo cuál es la mejor acción que ha de realizar sin saber cuál será la acción que el contrario realizará al mismo momento. Esto da la posibilidad de que en un mismo turno se puedan guardar hasta 4 estados del tablero con su respectiva etiqueta, es decir, uno por cada jugador, por lo que se pueden crear conjuntos de datos más grandes en menos partidas y, por lo tanto, en menos tiempo.
De las partidas reales extraídas, se ha guardado el estado actual del tablero y el movimiento que ha realizado cada agente para que, en el momento de codificar la entrada para la red neuronal, haya cuatro visiones y cuatro decisiones distintas para un mismo estado, es decir, una por cada agente.
Entrada y salida de la red neuronal
Una vez obtenido el conjunto de datos de entrenamiento, es necesario codificar las variables y las acciones a una estructura válida para las redes neuronales. Recordemos que los datos de entrada a la red neuronal contienen el estado actual del tablero, el cual se ha codificado en una matriz binaria de tamaño (11, 7, 17), es decir, 11 columnas, 7 filas y 17 canales. Esto quiere decir que cada celda del tablero de tamaño 11 x 7 está representada por 17 variables binarias. Cada canal de la matriz codifica una parte distinta de información del tablero.
El valor en la matriz, para todos sus canales, es 1 si la posición en el tablero se corresponde a la celda de la matriz que se quiere representar en el canal. El valor es 0 si no se quiere representar nada en esa posición de la matriz. Si un agente está muerto, los canales que representen la posición actual en el tablero tendrán todas sus celdas con el valor 0.
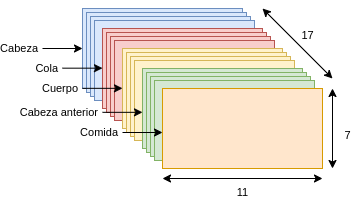
- Los primeros cuatro canales codifican las posiciones de las cabezas de cada agente, con un canal por agente. Cada canal es one-hot ya que hay, como mucho, un valor que no es 0.
- Los canales del 5 al 8 indican la posición de la cola de cada agente. Cada canal es one-hot.
- Los canales del 9 al 12 codifican las posiciones de los cuerpos enteros de cada agente. Estos canales no son one-hot.
- Los canales de 13 al 16 indican las posiciones que ocupaban las cabezas de los agentes en el anterior estado del tablero. Cada celda es one-hot.
- El canal 17 indica todas las posiciones que ocupa la comida, pudiendo haber una o dos piezas de comida a la vez.
Con este tipo de codificación, el modelo puede inferir la longitud y forma del agente desde la posición de la cabeza, cuerpo y cola. Además, la dirección que ha tomado con respecto a la última posición de la cabeza y la posición de los demás agentes para evitar colisiones.
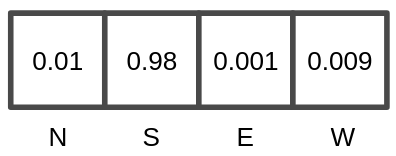
La salida de la red neuronal es una matriz de 1×4 con las probabilidades de realizar cada una de las 4 acciones posibles que tiene el juego (NORTH, SOUTH, EAST o WEST). La acción con la probabilidad más alta es la que finalmente se realiza dado el estado actual del tablero en cada turno.
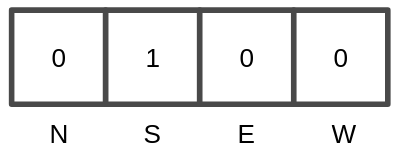
Para la fase de entrenamiento, se utiliza una matriz 1×4 one-hot con la acción realizada durante la obtención del conjunto de datos dado un estado del tablero.
Arquitectura de la red neuronal
La red neuronal implementada consiste en un primer bloque, llamado bloque convolucional, que se repite 6 veces, seguido de una capa Global Average Pooling [3], para minimizar la posibilidad de overfitting reduciendo el número de parámetros en el modelo, y finalizando con dos capas de neuronas completamente conectadas de 1024 y 512 neuronas, respectivamente, cuya función de activación es Leaky ReLU. La capa de salida consta de 4 neuronas, que son las cuatro posibles acciones que puede realizar el agente. La arquitectura completa de la red neuronal se puede ver en la siguiente figura.
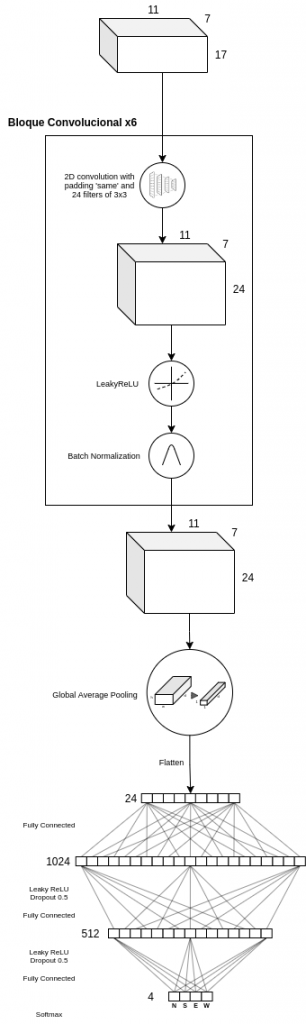
El bloque convolucional consiste en una capa convolucional de dos dimensiones, con un padding automático que permite que la entrada y salida de esta capa sean iguales en altura y anchura, y 24 filtros de 3×3.
Como se ha explicado anteriormente, el tamaño de la entrada del modelo es (11, 7, 17), por lo que al aplicar padding automático y 24 filtros de 3×3, la salida de la capa convolucional será de (11, 7, 24). A continuación, se aplica la función de activación Leaky ReLU. Por último, se usa una capa Batch Normalization para estandarizar la salida de la capa convolucional hacia la entrada de la siguiente capa, transformando los valores a media 0 y desviación estándar 1. Batch Normalization permite usar un learning rate más alto sin que haya un riesgo de divergencia, además de regularizar el modelo y reducir la necesidad de usar Dropout [1, 2]. Este mismo bloque se repite 6 veces más, obteniendo un salida final de tamaño (11, 7, 24).
Finalmente, se aplican dos capas ocultas de neuronas completamente conexas, de 1024 y 512 neuronas, respectivamente, con una función de activación Leaky ReLU y un Dropout de 0.5.
Entrenamiento
El optimizador usado en el modelo es Stochastic Gradient Descent with Momentum (SGDM) [4, 5], debiendo ajustar los parámetros learning rate y momentum. El entrenamiento empieza con un learning rate fijo a 0.01 que decrece por un factor constante de 0.3 cuando no hay una mejora en el modelo en un número determinado de epochs, hasta un mínimo de 0.0001, mientras que el parámetro momentum se mantiene constante durante todo el entrenamiento a 0.9 [6].
En 10 epochs se ha llegado a un accuracy de 0.75 en el conjunto de datos de validación, es decir, en los registros que no se han usado ni para entrenar ni para testear. En 13 epochs se ha obtenido un accuracy de 0.8102, no habiendo nada de mejora en los siguientes 25 epochs, por lo que el entrenamiento se ha detenido. El resultado final en una partida real en la que los 4 gansos usan la misma red neuronal convolucional entrenada es el siguiente:
Como se puede observar, el modelo ha sabido inferir que el ganso debe evitar el contacto consigo mismo y con sus rivales, que debe ir a por la comida para no morir y ganar e, incluso, protegerse. A partir del paso 95 es posible ver que el ganso azul da vueltas sobre sí mismo como mejor opción para evitar colisionar con los rivales que tiene a su alrededor. Por otro lado, a partir del paso 104 se puede observar que el ganso blanco no coge la comida que tiene al lado suya porque sabe que acabará en un espacio cerrado del que no podrá salir.
Espero que os haya gustado este artículo en el que se explica cómo fácilmente se puede implementar una inteligencia artificial básica con redes neuronales convolucionales que sea capaz de competir y con la que se pueden ver unos resultados inmediatos del entrenamiento realizado. El repositorio en el que se ha implementado esta red neuronal, además de otras implementaciones, lo podéis encontrar aquí.
Si quieres conocer más acerca de redes neuronales, aconsejo leer los siguientes artículos que han realizado otros miembros de Damavis:
- Perceptrón Simple: Definición Matemática y Propiedades
- El Perceptrón Simple: Implementación en Python
- Creación de una red convolucional con Tensorflow
Bibliografía
[1] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15(56): 1929–1958, 2014.
[2] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. CoRR, abs/1502.03167, 2015.
[3] Min Lin, Qiang Chen and Shuicheng Yan. Network in network. In 2nd International Conference on Learning Representations, Conference Track Proceedings, Banff, AB, Canada, 2014.
[4] B.T. Polyak. Some methods of speeding up the convergence of iteration methods. USSR Computational Mathematics and Mathematical Physics, 4(5):1–17, 1964
[5] Nicolas Loizou and Peter Richtárik. Momentum and stochastic momentum for stochastic gradient, newton, proximal point and subspace descent methods. Computational Optimization and Applications, 77, 12 2020.
[6] Kaiming He, Xiangyu Zhang, Shaoqing Ren and Jian Sun. Deep residual learning for image recognition. CoRR, abs/1512.03385, 2015.
Te animamos a compartir este post con todos tus contactos. No olvides mencionarnos para poder conocer tu opinión. ¡Hasta pronto!

