El Perceptrón Simple: Implementación en Python

En la actualidad, las redes neuronales artificiales son una de las principales líneas de estudio en el campo de la inteligencia artificial. Esta familia de algoritmos permite resolver tareas tan complejas y diversas como el reconocimiento de imágenes, el procesamiento de lenguaje natural o la generación de música. La principal unidad constituyente de estos modelos es el perceptrón simple, que, en esencia, imita el funcionamiento básico de una neurona biológica.

En el Perceptrón Simple: Definición Matemática y Propiedades, ya abordamos qué es y cómo se define el perceptron. A continuación, veremos cómo funciona y cómo puede implementarse en Python.

¿Qué es y cómo funciona el perceptrón?

Partimos de un conjunto de datos de entrada, cada uno con una serie de variables independientes o explicativas = (x₁,… ,x_N) y una variable dependiente u objetivo 𝑦. La finalidad del perceptrón es aprender a predecir la variable 𝑦 a partir de las variables . Para ello, necesita aprender de un conjunto de datos llamado el conjunto de entrenamiento. Así, dada una observación (⁽ⁱ⁾, 𝑦⁽ⁱ⁾), el modelo emite una predicción ŷ⁽ⁱ⁾ según la función

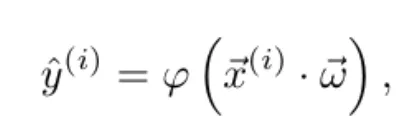
donde φ es la función de activación y = (ω₁,…,ω_N) es el vector de pesos, que se inicializa aleatoriamente.

Aprendizaje del modelo

¿Cómo aprende el modelo? Tras cada ejemplo de entrada, se compara el valor predicho con el valor real. De esta forma, se cuantifica el error cometido mediante una función de costes (o función de pérdidas) 𝐽(ŷ⁽ⁱ⁾, 𝑦⁽ⁱ⁾). Notemos que, dado un vector de entrada ⁽ⁱ⁾, el valor predicho depende únicamente de los pesos. Por tanto, dado un ejemplo de entrenamiento (⁽ⁱ⁾, 𝑦⁽ⁱ⁾), la función de costes depende únicamente del vector de pesos, 𝐽 = 𝐽().

Así, conociendo el gradiente de la función de costes respecto de los pesos ∇𝐽(), podemos usar el descenso del gradiente para ir actualizando los pesos a medida que hacemos predicciones. De esta forma, se minimizará la función de costes.

Existen distintas variantes del descenso del gradiente, que dependen de la frecuencia con la que se actualizan los pesos. En el descenso del gradiente estocástico, los pesos se actualizan tras cada ejemplo de entrenamiento. Por otro lado, en el descenso del gradiente en minibatch, se actualizan tras cierto número de ejemplos. Y, por último, en el descenso del gradiente en batch, la actualización se produce tras cada epoch o bucle sobre todo el conjunto de entrenamiento. Así, la actualización de los pesos ^(𝑘) en cada iteración 𝑘 viene dada por la fórmula

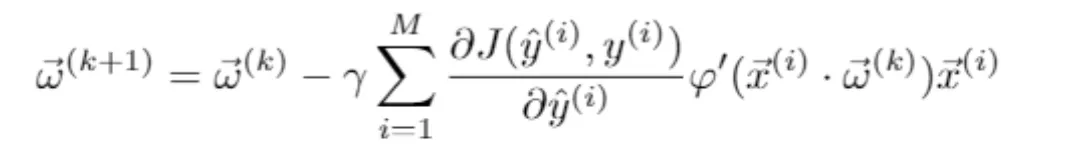
donde 𝛄 es el ratio de aprendizaje y el sumatorio recorre un número 𝑀 de ejemplos de entrenamiento, que depende de la modalidad del descenso del gradiente usada. Nótese que se ha usado la regla de la cadena para calcular el gradiente de la función de costes respecto al vector de pesos, ∇𝐽(^(𝑘)), en función del valor predicho ŷ⁽ⁱ⁾ = ŷ⁽ⁱ⁾(^(𝑘)).

Implementación del perceptrón en Python

Para ilustrar mejor todo el proceso descrito anteriormente, veamos un ejemplo concreto.

Ejemplo práctico: Predicción en el sector bancario

Imaginemos que trabajamos en un banco y queremos construir un modelo que prediga si un cliente devolverá un préstamo partiendo únicamente de dos variables independientes. Por un lado, el montante del préstamo concedido y, por otro, los ingresos mensuales del cliente. Para ello, necesitamos un conjunto de entrenamiento formado por muchas observaciones de clientes de los que conocemos estas dos variables, así como si devolvieron el préstamo o no. 

import pandas as pd
data = pd.read_csv("loan_data.csv")

data.head()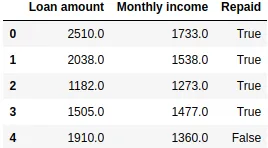

Tenemos un pandas.DataFrame en el que las primeras dos columnas representan, respectivamente, el montante del préstamo y los ingresos mensuales del cliente (expresados en ciertas unidades monetarias). La tercera columna contiene la variable dependiente, True si el préstamo fue devuelto y False si no.

Normalización de los datos

Es común que las distintas variables de nuestro dataset tengan distintos órdenes de magnitud. Por ello, es habitual realizar en primer lugar una normalización de los datos. En este caso, escalamos linealmente cada una de las variables numéricas en el intervalo [0, 1].

from sklearn.preprocessing import MinMaxScaler

indep_vars = ["Loan amount", "Monthly income"]
data[indep_vars] =  MinMaxScaler().fit_transform(data[indep_vars])
data.head()

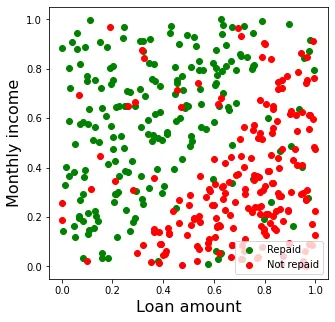
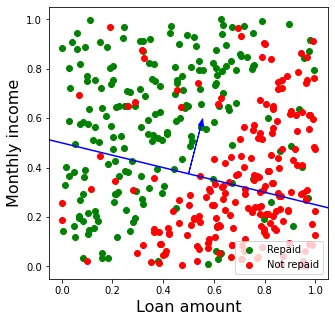
En la Figura 1 se muestra un gráfico de dispersión de los datos de los que disponemos. En general, se observa un patrón en los datos. El préstamo es devuelto en la mayoría de los casos en los que el montante es bajo en relación a los ingresos mensuales del cliente (parte superior izquierda del gráfico), mientras que no es devuelto en caso de que el montante sea relativamente alto (parte inferior derecha).

Función de activación logística

En este caso, puesto que tenemos una variable binaria, usaremos la función de activación logística, cuya expresión y la de su derivada vienen dadas por 

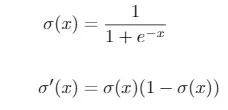
Esta función siempre da una salida entre 0 y 1. En el caso de clasificación binaria, puede interpretarse como la probabilidad ŷ = 𝑃 (𝑦 = 1). Además, la función es creciente y se cumple que σ(0) = 0.5.

Así pues, dada la combinación lineal entre pesos y variables independientes, 𝑧 = · , tendremos que σ(𝑧) = ŷ > 0.5 (y por tanto la predicción será 𝑦 = 1) si y sólo si se cumple que 𝑧 > 0. Es decir, el vector de pesos determina un hiperplano (en nuestro caso de dos dimensiones, una recta) que divide el plano en dos regiones. De esta forma, para todos los puntos de una región tenemos ŷ > 0.5 (en nuestro caso, predecimos que el préstamo será devuelto) y para todos los puntos de la otra región tenemos ŷ < 0.5 (predecimos que el préstamo no será devuelto).

Notemos que, si solo considerásemos tantos pesos como variables independientes (en nuestro caso, dos: ω₁ y ω₂), tendríamos la recta

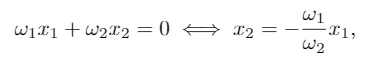
que siempre pasa por el origen de coordenadas. Para poder ajustar la ordenada al origen de la recta determinada por el vector de pesos (o en el caso de 𝑁 variables explicativas, el término independiente del hiperplano que divide el espacio en dos regiones), se suele introducir una variable adicional 𝑋₀ consistente en una columna de unos como entrada del modelo. De esta manera, su peso asociado ω₀ ajustará el término independiente del hiperplano.

División de variables y conjunto de datos

Así, separamos nuestro conjunto de datos en las variables independientes X y la variable objetivo y, la cual convertimos a numérica: (False, True)→(0,1). Asimismo, introducimos la variable adicional X0 como una columna de unos.

X = data[indep_vars]
y = data[["Repaid"]].astype(float)
X.insert(0, "X0", 1.)

X.head()
y.head()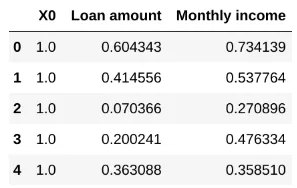

A continuación, dividimos el dataset en los conjuntos de entrenamiento, validación y test.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X.values, y.values, test_size=0.3)
X_train, X_validation, y_train, y_validation = train_test_split(X_train, y_train, test_size=0.3)

Definición del perceptrón simple

Ya estamos preparados para definir nuestro perceptrón simple. Por supuesto, existen librerías como scikit-learn o keras que contienen implementaciones de redes neuronales, incluyendo el sencillo caso del perceptrón. Por ejemplo, con las clases SGDRegressor o  SGDClassifier del módulo  sklearn.linear_model, podemos instanciar un perceptrón que use el descenso del gradiente estocástico (SGD, por sus siglas en inglés) dependiendo de si estamos frente a un problema de regresión o de clasificación, respectivamente. 

Sin embargo, para ilustrar mejor los conceptos, a continuación definiremos nuestra propia clase, a la que llamaremos SimplePerceptron. En este caso, usaremos la función de pérdidas cuadrática. Como vimos, su expresión y la de su derivada vienen dadas por

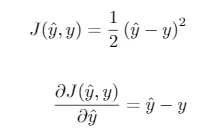
Otra elección común en el caso de clasificación binaria es la entropía cruzada binaria, dada por la ecuación

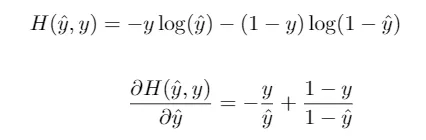
De hecho, combinando esta función de pérdidas con la función de activación logística, obtenemos el popular algoritmo de la regresión logística. 

Finalmente, usamos el descenso del gradiente en batch y fijamos un ratio de aprendizaje de 𝛾 = 0.1 fijo durante el entrenamiento.

class SimplePerceptron:
    learn_rate = 0.1

    def __init__(self):
        self.weights = None
        
    def logistic_function(self, x: float) -> float:
        """
        Logistic function, used as the activation function
        """
        return 1. / (1 + np.exp(-x))

    def forward_pass(self, X: np.ndarray) -> float:
        """
        Prediction of a single data point, given the current weights
        """
        weighted_sum = np.dot(X, self.weights)
        output = self.sigmoid_function(weighted_sum)

        return output

    def fit(self, X_train: np.ndarray, y_train: np.ndarray, n_epochs: int = 20):
        """
        Training using Batch Gradient Descent.
        Weights array is updated after each epoch
        """
        self.weights = np.random.uniform(-1, 1, X_train.shape[1])
        current_weights = self.weights.copy()
        for epoch in range(n_epochs):
            for x, y in zip(X_train, y_train):
                y_predicted = self.forward_pass(x)
                current_weights -= self.learn_rate * (y_predicted - y) * y_predicted * (1 - y_predicted) * x
            self.weights = current_weights.copy()

    def predict(self, X_test: np.ndarray) -> np.ndarray:
        """
        Predict label for unseen data
        """
        return np.array([self.forward_pass(x) for x in X_test])

Entrenamiento del modelo

A partir de aquí, podemos entrenar el modelo pasando los datos de entrenamiento a la función fit(). Una vez entrenado, podemos usar el método predict() para hacer predicciones sobre los datos de test. 

perceptron = SimplePerceptron()

perceptron.fit(X_train, y_train)
y_pred = perceptron.predict(X_test)

Para ver cómo se desarrolla paso a paso el proceso de aprendizaje, lo ilustraremos con los resultados de una ejecución concreta del comando anterior. En primer lugar se inicializa de forma aleatoria el vector de pesos, y obtenemos un valor ⁽¹⁾ = (-0.39, 0.21, 0.80). Este vector divide el plano en dos regiones, como muestra la Figura 3.

Con esta división, todos los puntos por encima de la recta se predicen como verdes (𝑦 = 1 o préstamo devuelto) y los que están por debajo como rojos (𝑦 = 0 o préstamo no devuelto). Evidentemente, al tratarse de una inicialización aleatoria del vector de pesos, el error cometido es alto.

En particular, todos los puntos en rojo por encima de la recta y todos los puntos en verde por debajo de ella serán incorrectamente clasificados. Esto da una precisión (número de aciertos dividido entre número total de ejemplos) sobre el conjunto de test de 0.575. Al ser 0.5 la precisión de una clasificación binaria aleatoria, se confirma que la clasificación inicial no es muy buena.

Función de pérdidas y predicciones

A continuación empieza el proceso de entrenamiento. En cada epoch se recorren todos los ejemplos de entrenamiento, calculando su predicción (Ecuación 1) usando el vector de pesos actual. Notemos que las correcciones en los pesos (Ecuación 2) se van guardando en la variable current_weights tras cada predicción. Sin embargo, como usamos el descenso del gradiente en batch, solamente al completar cada epoch se actualiza la variable self.weights, que es la que se usa para hacer las predicciones en el método forward_pass().

Al finalizar la primera epoch, la función de pérdidas sobre el total del dataset es de 𝐽(⁽¹⁾) = 46.37. Tras aplicar la primera actualización de los pesos obtenemos un nuevo vector de pesos ⁽²⁾ =(-0.46, -0.18,  0.98), calculado mediante la acumulación de las correcciones correspondientes a cada predicción. Así, en la segunda epoch obtenemos una función de costes 𝐽(⁽²⁾) = 44.70 que es inferior a 𝐽(⁽¹⁾), reflejando que hemos avanzado en la dirección de decrecimiento de la función. 

Este mismo procedimiento se repite para cada una de las epochs posteriores. De esta manera, se obtiene un valor de la función de costes cada vez menor.

Overfitting: Sobreajuste del modelo

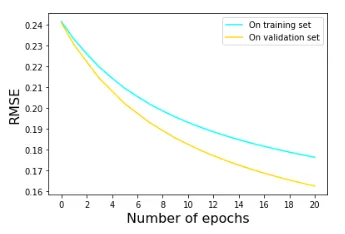
En la Figura 4 se muestra la evolución de la métrica RMSE (proporcional a la raíz cuadrada de la función de pérdidas) sobre los conjuntos de entrenamiento y de validación tras realizar 20 epochs.

En este caso, vemos que la función de pérdidas presenta una tendencia descendente tanto para el conjunto de entrenamiento como el de validación. Esto nos indica que no se ha producido overfitting. De hecho, salvo por una elección muy sesgada de los datos de entrenamiento, es difícil que un modelo tan sencillo como el perceptrón sobreajuste los datos.

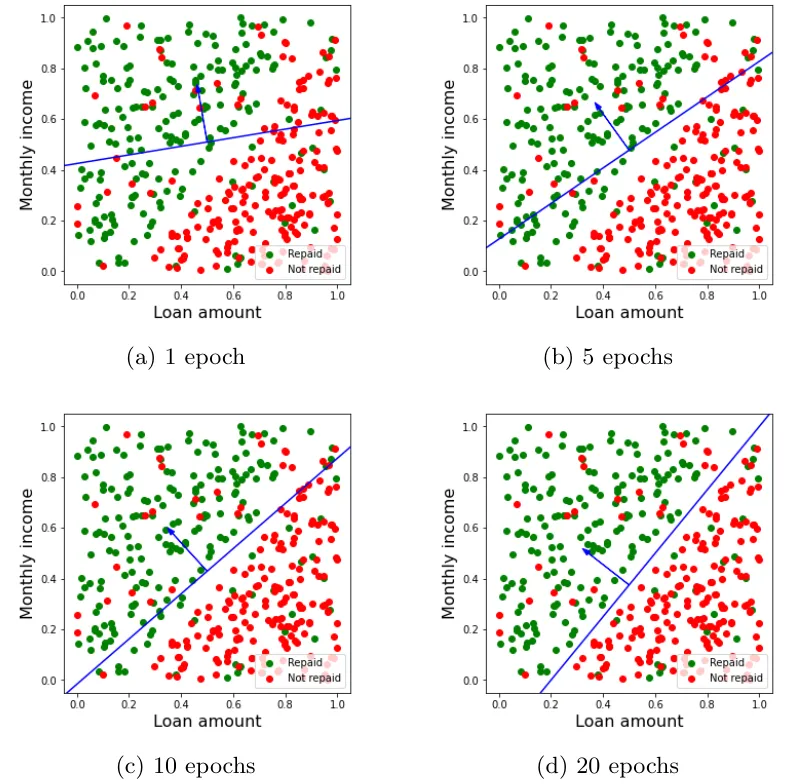
Finalmente, en la Figura 5 se muestra la evolución de la división del plano por el vector de pesos tras distintos números de epochs. Como vemos, si bien no se llega a conseguir una clasificación perfecta, al final del proceso de entrenamiento la recta determinada por los pesos es capaz de separar las dos clases mucho mejor que con el vector de pesos inicial, fruto de las correcciones introducidas al final de cada epoch.

Precisión del modelo

Tras este proceso, la precisión del modelo sobre el conjunto de entrenamiento es de 0.90, muy por encima del 0.575 inicial. La precisión sobre el conjunto de test es de 0.8875, muy cercana a la que se obtiene para el conjunto de entrenamiento, de nuevo señal de que no se han sobreajustado los datos de entrenamiento. Esto significa que, sabiendo los ingresos del cliente y el montante pedido, predeciremos correctamente si el préstamo será devuelto o no en unos 9 de cada 10 casos.

Notemos que, dado nuestro conjunto de datos, nunca podremos conseguir una precisión de 1.0 (lo que significaría no cometer ningún error de clasificación) con este modelo. Esto es debido a que los datos no son linealmente separables, es decir, no se pueden dividir los puntos verdes y rojos con una línea recta. De hecho, esta es una de las limitaciones fundamentales del perceptrón simple: al ser un modelo lineal (que usa combinaciones lineales de las variables de entrada, al igual que por ejemplo la regresión logística) solamente es capaz de aprender a la perfección conjuntos de datos que son linealmente separables en las variables explicativas.

Conclusión

En próximos posts hablaremos de cómo se construyen las redes neuronales artificiales mediante la combinación de perceptrones simples y cómo pueden ayudar a resolver problemas más complejos. En concreto aquellos desafíos en los que los datos no son linealmente separables. Mientras tanto, te animamos a visitar el blog de Damavis y ver artículos similares a este en la categoría Algoritmos.

Si te ha parecido útil este post, compártelo con tus contactos para que ellos también puedan leerlo y opinar. ¡Nos vemos en redes!