Imagine you are a data scientist working for a company that has decided to merge the databases of two of its departments into one. There is no common index between the two sources and the task is to ‘deduplicate’ the records or, in other words, to establish which record in one table corresponds to the same entity as another record in the other table in order to consolidate them into one:
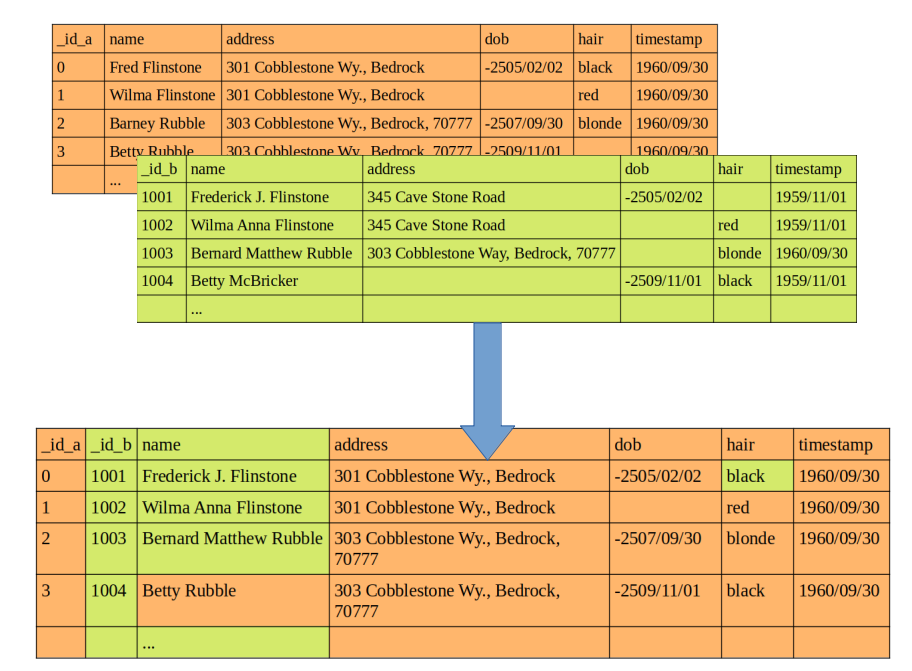
This process can be called by many names. In statistics it is known as record linkage and in computer science as data matching or entity resolution. A non-exhaustive list of more or less synonymous concepts in different contexts includes ‘purging processes’, ‘correlation resolution’, ‘fuzzy matching’ or ‘data integration’. In all cases it refers to the process of finding records corresponding to the same entity in different data sources, or in the same one.
The need for specific techniques for data linkage is always due to the absence of common and reliable identifiers between data sources. It is in these cases that data linkage is particularly useful, whatever the reason for the missing identifiers. For example, if census data from the 19th century are to be integrated for historical research purposes, it is very likely that no common identifier for individuals will be available.
In disadvantaged settings, official identifiers may also be missing to maintain a single medical record for all individuals attending hospitals in the same area. More common use cases in enterprises are Master Data Management processes to create golden records (typically of customers) and linkage processes for fraud detection in the financial sector.
Approaches to Record Linkage
There are two classic approaches to data binding:
Rule-based data linkage is the simplest approach to linking. This includes all rule systems that have been decided in advance to be the appropriate method for linking records. For example, in the absence of a common identifier, you can decide to link records as long as the concatenation of three fields is the same.
Another example would be that, from a number of possible common identifiers, two records are linked if there is a proportion of common identifiers greater than or equal to a predefined threshold X. Other approach would be to discretely give a number of possible common identifiers to each other. Another approach would be to discretionary weight the fields and decide that they are the same entity if their degree of linkage exceeds a certain threshold.
If, instead of giving weights to the fields in a deterministic way, these weights are computed with a model that takes into account the capabilities of the identifiers to determine whether or not there is linkage, we are dealing with a probabilistic type of linkage. In the simplest way, by defining a certain threshold, the user assumes that record pairs with a probability above this threshold are considered linked and those below it are not. Another option is to define two thresholds, between the values of which the record pairs that are ‘possible links’ are placed.
Fellegi and Sunter defined a first specific algorithm for linking records. It works by assigning specific weights (u and m) to each identifier where:
- u reflects the probability that the value of an identifier matches in a pair of unlinked records;
- m would be the probability that the value of the identifier matches for a pair of linked records.
For each identifier, u and m can be determined either by pre-analysis of the data or by running several iterations of the algorithm. These weights m and u are then used together with the overall linkage probability to compute the weights that will be used to calculate the probabilities. For a more in-depth explanation, Splink’s documentation on the Fellegi-Sunter model is a good resource.
The Fellegi-Sunter method is still widely used and has been extended to deal with some of its weaknesses (missing data, complex relationships between fields, etc.).
Notwithstanding these improvements, some researchers consider this algorithm to be equivalent to a naïve Bayes classifier (Wilson, 2011). It has also been observed that generic classification algorithms commonly used in machine learning such as logistic regression or support vector machines can match or even outperform it (Mason, 2018; Aiken et al. 2019).
Challenges of Record Linkage
In general, classical linking approaches are simple, easy to explain and work well with small datasets. Regardless of whether their results are better or worse than those of machine learning algorithms, their most notable weakness is their limited flexibility to adapt to changes in the data. Other challenges, somewhat common with any algorithm intended to be used for data linking, include:
- Dealing with variations and errors in identifier-specific values. String fields are very susceptible to typographical errors or small or large variations of the same value that make it difficult, a priori, to link them effectively. Together with a preprocessing of the text fields, string comparison or tokenised text distance algorithms can be useful to compute degrees of similarity between fields of this type in their possible pairings. Phonetic algorithms such as Soundex and Metaphone can also be useful for English text strings.
- Privacy issues. When legislation or corporate policy issues prevent sharing sensitive data, algorithms such as Bloom can encrypt sensitive string fields while preserving peer-to-peer similarity (Chi et al., 2017).
- Missing values can make the linking process more difficult than an erroneous or fuzzy value. When fields are numeric, it may be advisable to impute values before attempting to link the databases. In Chi et al., 2017, for example, KNN-neighbours is used to impute missing values.
- Handling issues of scale. The lack of common identifiers means that the space of comparisons can grow quadratically. To limit this growth, certain fields are often locked to avoid exploring linkages outside these fields. For example, if a reliable variable such as the CNAE (National Classification of Economic Activities) code is available in two supplier databases, locking it to avoid exploring linkages where this code is different limits the number of possible combinations.
Machine Learning Approaches
Classical data binding approaches can be very useful when the use case is simple and static. For example, when it has to be done only once with two small static tables, it may be sufficient to design a few rules that allow us to associate pairs of records. When tables have millions of rows, are constantly changing, there are complex relationships between fields or the data quality is poor, machine learning methods start to gain interest.
In the first instance, the pool of machine learning algorithms that can be used to link records depends on whether or not a labelled dataset is available for training.
- If available, any supervised learning algorithm with a classification objective can be used, from logistic regression to implementations of Extreme Gradient Boosting. Neural network-based methods can also be particularly useful for cases where non-linear relationships exist.
- If no labelled set is available, the options are restricted to unsupervised learning algorithms, in particular clustering. Graph-based clustering algorithms can be particularly useful if there are complex relationships or dependencies between entities.
Whatever algorithm is chosen, applying it to record linkage cases may require slightly different data preparation. First, decisions must be made to deal with the challenges outlined in the previous point.
In the case of using sorting algorithms, generating the training set requires cross-linking of records (or perhaps cross-linking by blocking certain fields). This can lead to a class imbalance that can be addressed by reducing the number of observations from the majority class (unlinked pairs) and giving more weight in training to observations from the minority class (linked pairs).
Before training, it is necessary to identify the set of common fields between sources and iterate over it to compute the degree of similarity between pairs of records in each field according to a previously established criterion, depending on the use case. It is on this set of similarities that the model is trained.
As for the evaluation in classification models, in many cases, due to the data contamination problems that can be generated, it makes more sense to do it based on measures of precision, recall or F1-score than to do it by accuracy.
On the other hand, if you are going to train a clustering model, it is important to do it correctly. The best way to do this is to generate a cross join of records (as in classification) by calculating the similarity between dimensions and then run the model to group the pairs into 2 clusters: match vs. no match.
Otherwise, training, deploying and monitoring the model should not make any difference compared to common machine learning use cases.
Linkage probabilities
There are two key issues to consider before attempting to resolve linkages:
- You need to know whether there may be duplicates in the tables themselves, before linking. It is not the same that, being so, a record in one table most probably corresponds to 2 other records in the other table, than, being so, we know in advance that there can be no duplicates.
- The degree of linkage between tables will almost never be 100%. There may be records in one or the other table that are not matched in their counterpart.
Taking this into consideration, after training a classification model, it is ready to check whether each combination of records is a real linkage or not. Most libraries have a predict_proba() or analogous method that returns predictions in the form of a probability. Depending on the use case, it may make sense to use these ordered probabilities before the binary output.
In the training of a clustering algorithm it has to be assumed that, even if only with a very high probability, each cluster corresponds to an entity. Then, soft clustering algorithms such as the Gaussian mixture model can be used to compute the probability that a record belongs to each cluster.
Depending on the specifics of the use case, we will have to decide how to solve cases where the linking probabilities are high for several entities at once. If we anticipate that there may be duplicates, we link all those above a certain probability threshold; if not, we may have to take the one with the highest probability. And we will almost certainly have records that we will not be able to link, because in most cases we will anticipate that the degree of linkage is not perfect.
Conclusion
Data linkage is not a new problem. Solving it with machine learning is not very new either, although it is more recent in time than classical approaches, either rule-based or probabilistic. In this post, the problem of record linkage and the challenges involved have been analysed at a very high level. On the other hand, we have reviewed the machine learning approaches that it may make sense to take to tackle the problem and the particularities involved in the stages of data preparation, evaluation and interpretation of probabilities.
Bibliography
Mason, L. G. (2018). A comparison of record linkage techniques. Quarterly Census of Wages and Employment (QCEW): Washington, DC, USA, 2438-2447.
Aiken, V. C. F., Dórea, J. R. R., Acedo, J. S., de Sousa, F. G., Dias, F. G., & de Magalhães Rosa, G. J. (2019). Record linkage for farm-level data analytics: Comparison of deterministic, stochastic and machine learning methods. Computers and Electronics in Agriculture, 163, 104857.
Wilson, D. R. (2011, July). Beyond probabilistic record linkage: Using neural networks and complex features to improve genealogical record linkage. In The 2011 international joint conference on neural networks (pp. 9-14). IEEE.
Chi, Y., Hong, J., Jurek, A., Liu, W., & O’Reilly, D. (2017). Privacy preserving record linkage in the presence of missing values. Information Systems, 71, 199-210.
And that is all! If you found this post interesting, we encourage you to visit the Data Analytics category to see all the related posts and to share it on your networks. See you soon!

