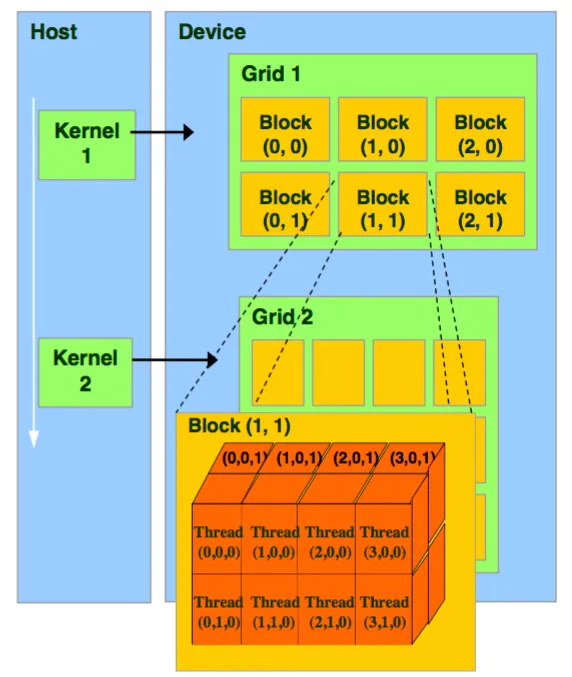
In the first part of the CUDA Tutorial, we mentioned the GPU’s smallest unit of execution, warps, the equivalent of a kernel on a CPU. However, warps alone cannot harness the full power of the GPU; you need to make use of the abstractions above the warps: blocks and grids.
This execution model only makes sense if the code is divisible into small tasks, which execute the same code, but contribute to the overall task. Therefore, for the examples that will be described in this article, we will continue with the use case of the kernel aggregating elements that we already saw in the tutorial of the previous post.
All code invoking CUDA kernels is in Python using Pycuda.
Blocks in CUDA
A block is an ordered group of threads executed by a Streaming Multiprocessor (SM). Each thread is identified by a unique ID based on its position within this block, and these blocks, in turn, can never have more than 1024 threads.
As an example, we have a perfectly valid kernel that, using a reduction, obtains the sum of a vector and executes without generating any error with 256 threads.
__global__ void sum(float *a)
{
int idx = blockDim.x*blockIdx.x+threadIdx.x;
float val = a[idx];
__shared__ float shared_mem[8];
for (int offset = 16; offset > 0; offset /= 2) {
val += __shfl_down_sync(0xffffffff, val, offset);
}
if(threadIdx.x%32==0) {
shared_mem[threadIdx.x>>5]=val;
}
__syncthreads();
if (threadIdx.x<=8) {
val=shared_mem[threadIdx.x];
val += __shfl_down_sync(0xffffffff, val, 4);
val += __shfl_down_sync(0xffffffff, val, 2);
val += __shfl_down_sync(0xffffffff, val, 1);
if (threadIdx.x==0) {
a[0]=val;
}
}
}Next, we invoke the kernel with the following calls to Pycuda.
func = mod.get_function("sum") # Obtain kernel
func(a_gpu, block=(256,1,1)) # Execute kernel with a single block of specified sizeIf we run the process with 256 threads, it executes without giving any errors.
func = mod.get_function("sum") # Obtain kernel again
func(a_gpu, block=(2048,1,1)) # Execute with single block of 2048 threadsNow, we will indicate that a block contains 2048 threads on the X axis. What will happen is that CUDA will be unable to execute the kernel and will throw the following error message:
LogicError: cuFuncSetBlockShape failed: invalid argument
Therefore, if we want to run more than 1024 threads at a time, we need to run the kernel using more blocks. However, before adding more blocks, we must first remember some properties that these elements possess.
As part of the architecture, a block has a shared memory that every thread belonging to this block can access, called ‘shared memory’. This memory is, in essence, a user-managed cache that can also be used to communicate between threads.
For example, it may be the case that one warp writes a result to a vector in shared memory, then, another warp could read that value being extremely faster than if the write had been done in global memory. This is a common strategy in reduction algorithms and can be seen in the kernel above where we declare with __shared__ a vector that goes into shared memory. We can also see how in the kernel we use this shared memory to communicate between warps while doing a reduction sum, by forcing only one thread of each warp to write its result sequentially to memory.
shared_mem[threadIdx.x>>5]=valBlocks also come with a synchronisation mechanism, the __syncthreads() function, which allows any thread belonging only and exclusively to this block to be synchronised at the time that function is called.
The threads within a block are organised as a matrix of 3 dimensions, X, Y and Z, and the user is in charge of giving the dimensions of this matrix, taking into account that it cannot exceed 1024 threads. In the kernel we can observe this with the use of threadIdx.x, which indicates the position of that thread in the X dimension of this matrix.
What are Grids in CUDA?
A grid is an ordered group of blocks and each block has a unique ID based on its position within the grid. Its organisation is similar to how blocks organise threads.
The grid allows algorithms that use more than 1024 threads to run, otherwise it would be impossible due to the limit of threads in a block.
The grid blocks are organised as a 3-dimensional array, X, Y and Z, where the user has to assign the dimensions taking into account that each block contains an array of threads.
func = mod.get_function("sum")
func(a_gpu, block=(256,1,1), grid=(8,2,10))For example, here we run a kernel with 256 threads and a grid of 160 blocks, 8 in X, 2 in Y and 10 in Z dimension. In total, a kernel with 40960 threads.
Contrary to the block case, the grid has no mechanism for synchronisation. What happens between different blocks of a grid is independent and cannot be coordinated within the same call.
func = mod.get_function("sum")
func(a_gpu, block=(256,1,1), grid=(8,1,1))
a_sum = numpy.empty_like(a)
cuda.memcpy_dtoh(a_sum, a_gpu)For example, in this code we execute the above kernel in 8 different blocks, but as the code has no way of talking about the work between blocks, we find that it has written 8 times the result of the sum of a block in the same memory location. In turn, we could not simply add in that global memory location, since, as there is no synchronisation, we could be overwriting the different blocks.
Therefore, a common way to achieve a similar effect to synchronising blocks is to chain different function calls, because if they are sent to the same CUDA stream, they will be executed in order, so the result will be synchronised before executing the next function.
__global__ void sum(float *a)
{
int idx = blockDim.x*blockIdx.x+threadIdx.x;
float val = a[idx];
__shared__ float shared_mem[8];
for (int offset = 16; offset > 0; offset /= 2) {
val += __shfl_down_sync(0xffffffff, val, offset);
}
if(threadIdx.x%32==0) {
shared_mem[threadIdx.x>>5]=val;
}
__syncthreads();
if (threadIdx.x<=8) {
val=shared_mem[threadIdx.x];
val += __shfl_down_sync(0xffffffff, val, 4);
val += __shfl_down_sync(0xffffffff, val, 2);
val += __shfl_down_sync(0xffffffff, val, 1);
if (threadIdx.x==0) {
a[blockIdx.x]=val;
}
}
}Altering the previous kernel, we now write the result to different global memory locations.
func = mod.get_function("sum")
func(a_gpu, block=(256,1,1), grid=(8,1,1))
cuda.memcpy_dtoh(a_sum, a_gpu)
print(sum(a_sum[0:8]) - sum(a))
# Result is close to 0 (hardware inaccuracies).With this we get the 8 elements in their correct position, but we want to add these remaining 8 elements on the GPU. One way to do this would be, for example, with a small kernel that will run after the one we have previously defined, in the previous code block.
__global__ void sum_small(float *a)
{
float val = a[threadIdx.x];
if (threadIdx.x<=8) {
val += __shfl_down_sync(0xffffffff, val, 4);
val += __shfl_down_sync(0xffffffff, val, 2);
val += __shfl_down_sync(0xffffffff, val, 1);
if (threadIdx.x==0) {
a[0]=val;
}
}
}In this case, we have a simple kernel that only adds up to 8 elements.
func(a_gpu, block=(256,1,1), grid=(8,1,1))
func_small(a_gpu, block=(8,1,1), grid=(1,1,1))
cuda.memcpy_dtoh(a_sum, a_gpu)
print (a_sum[0] - sum(a))
# Result is close to 0 (hardware inaccuracies).By chaining both kernel invocations, we can now get the full sum.
Grids: Practical example
Finally, we can see an example of how to coordinate several kernel runs with different grids to do a sum of a simple 2^24 element vector, and compare it with Numpy and pure Python in efficiency.
__global__ void sum(float *a)
{
int idx = blockDim.x*blockIdx.x+threadIdx.x;
float val = a[idx];
__shared__ float shared_mem[8];
val += __shfl_down_sync(0xffffffff, val, 16);
val += __shfl_down_sync(0xffffffff, val, 8);
val += __shfl_down_sync(0xffffffff, val, 4);
val += __shfl_down_sync(0xffffffff, val, 2);
val += __shfl_down_sync(0xffffffff, val, 1);
if(threadIdx.x%32==0) {
shared_mem[threadIdx.x>>5]=val;
}
__syncthreads();
if (threadIdx.x<=32) {
val=shared_mem[threadIdx.x];
val += __shfl_down_sync(0xffffffff, val, 4);
val += __shfl_down_sync(0xffffffff, val, 2);
val += __shfl_down_sync(0xffffffff, val, 1);
if (threadIdx.x==0) {
a[blockIdx.x]=val;
}
}
}The kernel is the usual kernel, but with the slight optimisation of moving the for to 5 separate instructions.
func(a_gpu, block=(256,1,1), grid=(65536,1,1))
func(a_gpu, block=(256,1,1), grid=(256,1,1))
func(a_gpu, block=(256,1,1), grid=(1,1,1))Adding the whole vector is as simple as calling the function 3 times with different numbers of blocks.
Compared to the time it takes to sum in Numpy and Python, the GPU is 8.1 times faster than Numpy with this implementation and 2295.5 times faster than pure Python. Note that these results depend on the hardware used, in this case, using an underpowered GPU.
It is only 8 times faster than the Numpy implementation, as it makes use of highly optimised code including AVX instructions to operate more efficiently on vectors.
Conclusion
We have seen what blocks and grids are, allowing us to organise threads over warps and dividing the work into small tasks that each thread executes depending on its position given its block in the grid and its thread within the block.
This system for organising threads allows us to design highly parallel programs natively that, even compared to highly optimised code that makes use of every possible benefit that the hardware offers, such as AVX instructions, are still more than 8 times faster. At the same time, it limits us in the typical number of tasks that can be executed, as these have to be compatible with the CUDA execution model.
